Неявно и параметрически
Уравнение
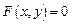 (17.4)
(17.4)
задает неявно функцию 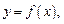 если при подстановке выражения f(x) вместо y в уравнение (17.4) оно превращается в тождество. Предположим, что функция
если при подстановке выражения f(x) вместо y в уравнение (17.4) оно превращается в тождество. Предположим, что функция 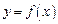 дифференцируема и требуется вычислить производную
дифференцируема и требуется вычислить производную 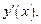
Первый способ. Если практически возможно, выражают y через x и дифференцируют y(x) по правилам дифференцирования.
Второй способ. Дифференцируют уравнение (17.4) по x, считая, что y есть функция от x. Получают новое уравнение, содержащее x, y и 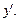 Из него находят
Из него находят 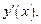
Пусть функция 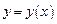 задана параметрически уравнениями:
задана параметрически уравнениями:
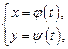
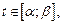 (17.5)
(17.5)
где функции 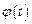 и
и 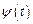 дифференцируемы для любого
дифференцируемы для любого 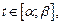 причем
причем 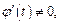 и требуется найти
и требуется найти 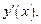
Первый способ. Из первого уравнения системы (17.5) выражают t через x (если это возможно) и подставляют во второе уравнение системы (17.5). Приходят к сложной функции от переменной x, которую дифференцируют по x.
Второй способ. Используют формулу
 (17.6)
(17.6)
Полученное таким образом выражение для 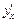 зависит от переменной t. Если возможно (и необходимо) из первого уравнения системы (17.5) выражают t через х и подставляют в выражение, полученное для
зависит от переменной t. Если возможно (и необходимо) из первого уравнения системы (17.5) выражают t через х и подставляют в выражение, полученное для 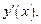
Пример 1.Найти производную 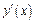 функции, используя возможные способы:
функции, используя возможные способы:
1) 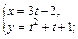 2)
2) 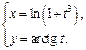
Решение. 1) 1-й способ. Из первого уравнения системы выразим t через x:
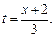
Полученное выражение подставим во второе уравнение вместо t:
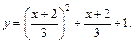
Получили функцию одной переменной х. Дифференцируем ее:
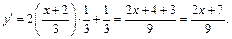
2-й способ. Используем формулу (17.6):
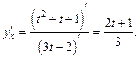
В полученное выражение подставив 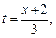 получим:
получим:
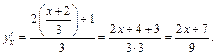
2) 1-й способ. Выразим из первого уравнения системы переменную t:
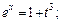
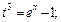
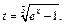
Подставляя найденное выражение для t во второе уравнение системы, получим сложную функцию переменной х: 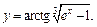 которую продифференцируем по правилу вычисления производной сложной функции:
которую продифференцируем по правилу вычисления производной сложной функции:

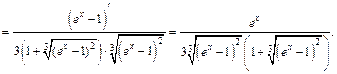
2-й способ. Воспользуемся формулой (17.6):

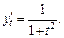
Подставляя выражения в формулу (17.6), получим:
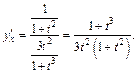
Подставляя  получим:
получим:
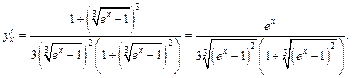
Пример 2.Вычислить значение производной параметрически заданной функции 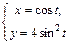 в точке
в точке 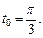
Решение.Функция 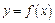 задана параметрически. Дифференцируем ее, используя формулу (17.6).
задана параметрически. Дифференцируем ее, используя формулу (17.6).
Вычислим: 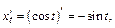
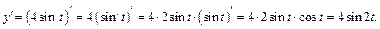
Подставим полученные выражения в формулу (17.6):
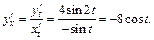
Найдем значение производной в заданной точке. Подставим значение 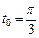 в полученное выражение:
в полученное выражение:
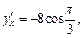 т. е.
т. е. 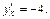
Пример 3.Вычислить 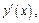 используя возможные способы:
используя возможные способы:
1) 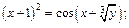 2)
2) 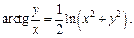
Решение. 1) Данное уравнение задает неявно функцию 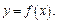 Продифференцируем ее двумя способами:
Продифференцируем ее двумя способами:
1-й способ. Выразим из уравнения у через х:
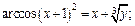
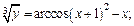
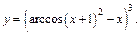
Продифференцируем выражение по переменной х:
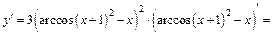
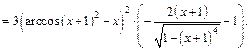
2-й способ. Продифференцируем обе части уравнения по переменной х, считая, что у есть функция от х:
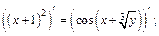
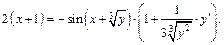
Откуда выразим 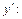
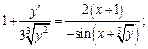
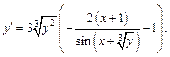
При необходимости можем выразить у через х из заданного равенства и подставить в полученное выражение.
2) Функция  задана неявно и в данном случае проблематично выразить переменную у через х, поэтому дифференцируем обе части равенства, учитывая, что y есть функция аргумента x:
задана неявно и в данном случае проблематично выразить переменную у через х, поэтому дифференцируем обе части равенства, учитывая, что y есть функция аргумента x:
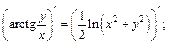
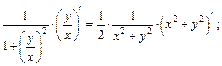
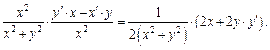
Из полученного равенства выразим 
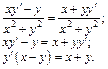
Приходим к ответу: 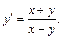
Дата добавления: 2015-09-29; просмотров: 1181;
