Непараметрические методы оценки корреляционной связи показателей
При исследовании степени тесноты связи между качественными признаками, каждый из которых представлен в виде альтернативных признаков, возможно использование следующих расчетных таблиц.
| a | b | a+b |
| c | d | c+d |
| a+c | b+d | a+b+c+d |
Строятся следующие показатели:
а) коэффициент ассоциации Д.Юла
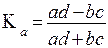
б) коэффициент контингенции К.Пирсона
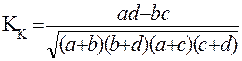
Пример.
«Исследование социальных аспектов трудовой деятельности работников»
Распределение по полу и оценка содержания работы.
| Работа | Мужчины | Женщины | Всего |
| Интересная | 300(a) | 201(b) | 501(a+b) |
| Неинтересная | 130(c) | 252(d) | 382(c+d) |
| Итого: | 430(a+c) | 453(b+d) | 883(a+b+c+d) |
Коэффициент ассоциации
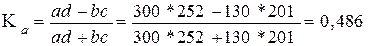
Величина коэффициента соответствует среднему размеру связи, несмотря на различие мнений о своей работе мужчин и женщин. Когда один из показателей 4-клеточной таблицы отсутствует, величина Ка=1, что дает преувеличенную оценку степени тесноты связи между признаками.
Коэффициент контингенции
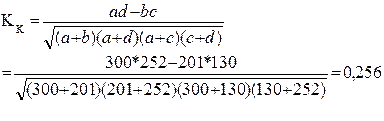
Кk<Ka
Связь между заинтересованностью работой мужчин и женщин считается подтвержденной, если Ка≥0,5 или Kk≥0,3.
Пример.
Исследуется связь между успеваемостью студентов-заочников одного из ВУЗов и работой их по специальности. Результаты обследования характеризуются следующими данными.
Зависимость успеваемости студентов-заочников от работы их по специальности.
| Студенты-заочники | Число студентов | из них | |
| получ. полож. оценки | получ. неуд. оценки | ||
| раб. по специальности | |||
| не раб. по спец. | |||
| Всего: |
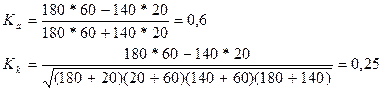
Таким образом связь между успеваемостью студентов-заочников и работой их по специальности существенна.
Коэффициент взаимной сопряженности Пирсона и Чупрова.
Если по каждому из двух взаимосвязанных признаков выделяется число групп больше 2-х, то для подобного рода таблиц теснота связи между качественными признаками может быть измерена с помощью показателей взаимной сопряженности Пирсона и Чупрова.
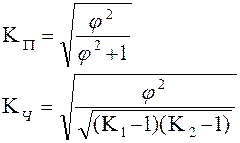
где в обеих формулах φ2 – показатель взаимной сопряженности, его рассчитывают как сумму отношений квадратов частот каждой клетки к произведению итоговых частот столбца и строки минус 1, т.е. если в таблице частоты внутри клеток обозначить nij, где i – номер строки, а j – номер графы, итоговые частоты по строкам - Ni , а по графам Nj. К1 и К2 – число групп в строках и графах.
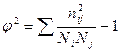
Пример.
С помощью коэффициентов взаимной сопряженности исследовать связь между себестоимостью продукции и производительностью труда.
| с/с i | произв.тр. j | производительность труда | Итого: Nj | |
| высокая | средняя | низкая | ||
| высокая | 19 n11 | 12 n12 | 9 n13 | |
| средняя | 7 n21 | 18 n22 | 15 n23 | |
| низкая | 4 n31 | 10 n32 | 26 n33 | |
| итого: | 30 Ni | 40 |
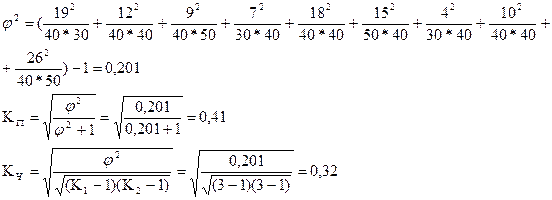
Связь средняя.
Литература:
Спирин А.А., Башина О.Э. Общая теория статистики. – М.: Финансы и статистика. 1995г. с. 237 – 277.
Дата добавления: 2015-09-11; просмотров: 1217;
