Коэффициенты корреляции рангов. Наряду с r и η для измерения тесноты зависимости между коррелируемыми показателями часто используются так называемые эмпирические показатели
Наряду с r и η для измерения тесноты зависимости между коррелируемыми показателями часто используются так называемые эмпирические показатели, которые называются коэффициентом корреляции рангов:
1. Коэффициент Спирмэна (p)
2. Коэффициент Кендэла (τ)
Оба эти показателя основаны на корреляции не самих значений (х и у), а их рангов.
Коэффициент корреляции рангов Спирмэна
Для расчета коэффициентов корреляции рангов Спирмэна значения случайных величин х и у нумеруются (каждое отдельно) в порядке возрастания (или убывания) от 1 до n, т.е. им присваивается определенный ранг (Nх и Nу) – порядковый номер в ряду. Если встречается несколько одинаковых значений х (или у), то каждому значению присваивается ранг, равный частному от деления суммы рангов, приходящихся на эти значения, на число этих равных значений.
Затем ранги отдельных значений факторного признака сопоставляются с рангами результативного признака.
Разность рангов (Nx-Ny) обозначают d. Степень тесноты связи между изучаемыми признаками в этом случае можно определить по формуле Спирмэна
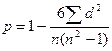
где d – разность рангов х и у
n – число пар наблюдений.
Коэффициент корреляции рангов Спирмэна р находится в пределах от 0 до ±1. Когда ранги результативного признака полностью совпадают с рангами факторного признака, то каждое значение Nx=Ny и ∑d2=0, тогда р = 1, то можно говорить о почти полной прямой связи. Если ранги идут строго в противоположном направлении, т.е. первому рангу фактора х соответствует n-й ранг (последний) результативного признака у, второму рангу х соответствует n-1 ранг у и т.д., то в этом случае максимальная величина будет равна
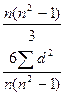
может иметь максимальное значение 2.
И тогда по формуле Спирмэна р=-1, что свидетельствует почти о полной обратной связи между х и у.
Если же связь между изменениями х и у отсутствует (р=0), то очевидно, в этом случае должно наблюдаться равенство.
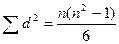
Этот показатель менее точен по сравнению с r и η. Расчет показателя прост, поэтому ему отдают предпочтение.
Пример.
| производственные основные фонды, млн.р. х | валовая продукция, млн.р у | Nx | Ny | d=Nx-Ny | d2 |
| 60,5 | 836,4 | 10,5 | 0,5 | 0,25 | |
| 40,7 | 836,4 | 10,5 | -0,5 | 0,25 | |
| 33,8 | 303,0 | -2 | |||
| 22,1 | 134,9 | 1,5 | 2,5 | 6,25 | |
| 33,8 | 139,3 | ||||
| 33,8 | 265,0 | ||||
| 20,9 | 1,5 | -2,5 | 6,25 | ||
| 35,9 | 287,2 | ||||
| 21,6 | 189,9 | 5,5 | -2,5 | 6,25 | |
| 22,4 | 189,9 | 5,5 | -0,5 | 0,25 | |
| 20,9 | 134,9 | 1,5 | 1,5 | ||
| ∑ | 40,5 |
Находим коэффициент Спирмэна 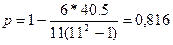
Зависимость между стоимостью основных фондов и выпускаемой продукции сильная.
Коэффициент Кендэла (τ)
Для расчета значения ранжируются. Затем определяют меру соотношения последовательности рангов у последовательности рангов х.
При этом для каждого ранга у определяют число следующих за ним значений рангов, превышающих его величину. Сумму чисел таких превышений обозначаем Р и будем считать со знаком (+). Аналогично для каждого ранга (у) определяют число следующих за ним рангов, имеющих значение меньше его величины. Сумма чисел таких случаев обозначаем через Q и будем считать со знаком (-).
Очевидно, что Р достигает максимума в том случае, если ранги у точно совпадают с рангами х. Если число пар рангов равно n, то максимальное значение слагаемого Р будет равно:
Рmax=(n-1)+(n-2)+…+3+2+1=n(n-1)/2
Соответственно слагаемое Qmax тоже имеет максимум абсолютного значения,
если последовательность вариантов у имеет обратную тенденцию по отношению к последовательности рангов вариантов х.
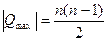
Коэффициент Кендэла (τ) предполагает измерение меры соот-ия последовательности рангов двух переменных путем сравнения общего итога ∑ положительных и отрицательных баллов (S=P+Q) с максимальным значением одного из слагаемых, т. е. 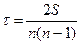
Пример:
| Производ. фонды, млн.р. х | валовая продукция, млн.р. у | Nx | Ny | d=Nx-Ny | d2 |
| 1,2 | 2,8 | ||||
| 1,6 | 4,0 | -1 | |||
| 2,5 | 3,8 | ||||
| 3,8 | 6,5 | ||||
| 4,3 | 8,0 | ||||
| 5,5 | 10,1 | -1 | |||
| 6,0 | 9,5 | ||||
| 8,0 | 12,5 | ||||
| 9,1 | 18,3 | ||||
| 10,0 | 24,5 | ||||
| n=10 |
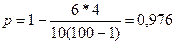
Рассчитаем коэффициент Кендэла
у: Р= 9+7+7+6+5+3+3+2+1=43
х: Q=0+(-1)+0+0+0+(-1)+0+0+0=-2
S=43-2=41
Тогда 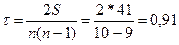
Получаемый коэффициент свидетельствует о значительной тесноте зависимости между изменениями значений х и у.
Данная формула применима для тех случаев, когда отдельные значения признака (х и у) не повторяются и следовательно, их ранги не объединены.
Дата добавления: 2015-09-11; просмотров: 765;
