Линейный коэффициент корреляции

В случае линейной зависимости между двумя коррелируемыми величинами тесноту связи измеряют линейным коэффициентом корреляции (r), который может быть рассчитан по нескольким формулам:

1.

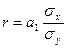
где а₁- коэффициент регрессии в управлении связи;

σ_х- среднее квадратическое отклонение факторного признака;

σ_у- среднее квадратическое отклонение результативного признака.

2.

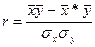
3.

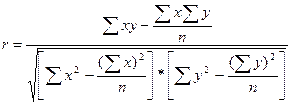
Рассчитаем линейный коэффициент корреляции по разным формулам:

основные произв. фонды, млн.р. х	валовая продукция, млн.р. у	х2	ху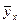
1,2	2,8	1,44	3,36	1,5
1,6	4,0	2,56	6,4	2,4
2,5	3,8	6,25	9,5	4,3
3,8	6,5	14,44	24,7	7,0
4,3	8,0	18,49	34,4	8,1
5,5	10,1	30,25	55,55	10,6
6,0	9,5	36,0	57,0	11,7
8,0	12,5	64,0		15,6
9,1	18,3	82,81	166,53	18,3
10,0	24,5			20,2
∑х=52	∑у=100	∑х2=356,24	∑ху=702,44

n=10

10а₀+52а₁=100

52а₀+356,24а₁=702,44

а₀=-1,024; а₁=2,12

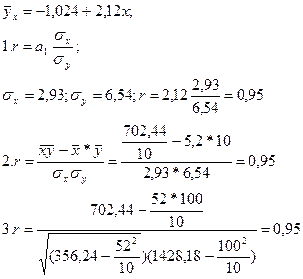
Линейный коэффициент корреляции может принимать значения от -1 до +1

Если r отрицательна – это обратная зависимость между х и у, т.е. с увеличением х уменьшается у и наоборот.

Если r =0 – связь отсутствует между х и у

Если 0 < r < 1 – связь функциональная.