Измерение тесноты связи

Кроме состав. уравн. регрессии для коррелируемых переменных второй задачей является измерение тесноты связи между ними. Измерить ее означает определить насколько вариация результативного признака зависит от вариации факторного. Измерить тесноту зависимости между х и у можно при помощи:

1. Корреляционного отношения (η) (коэффициент корреляции по Персону)

2. Линейного коэффициента корреляции (r)

Первый применим ко всем зависимостям, второй только при линейной зависимости.

а) корреляционное отношение различается:

1. теоретическое

2. эмпирическое

Теоретическое представляет собой относительную величину, получающуюся в результате сравнения среднего квадратического отклонения в ряду выравненных значений результативного признака ( 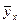), рассчитанных по уравнению регресии, со средним квадратическим отклонением в ряду эмпирических значений результатов признака.

первое – δ, второе – σ.

Учитывая, что выравненные эмпирические совпадают, т.е.

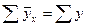и средние значения признака у рядов одинаково ( 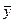), среднее квадратическое отклонение ряда выравненных значений результативного признака можно записать

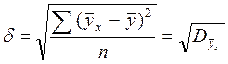
Если дисперсию выравненного σ ² обозначить через среднее квадратическое для эмпирического ряда результатов признака σ= 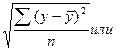σ ²=D_y, то корреляционное отношение можно записать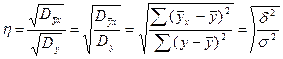

Возведя обе части в квадрат получим 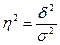; это корреляционное отношение называется коэффициентом детерминации. σ²=D_y, характеризует вариацию в ряду (у) за счет всех факторов, включая и фактор (х), а δ²= 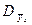характеризует вариацию результативного признака под влиянием фактора х. Если найдем отношение 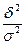, то получим малую долю, занимаемую дисперсией, определяемую влиянием факторного признака х. Т.е. в основе корреляционного отношения лежит правило сложения дисперсий .

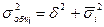При изучении корреляционных связей дисперсия в ряду 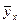и является межгрупповой дисперсией δ²= 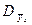ибо она отражает колеблемость групповых значений результативного признака (т.е. характерных для этой группы х) вокруг общей средней ряда, т.е. колеблемость за счет факторного признака.

Т.е. средняя из внутригрупповых дисперсий это и будет остаточная дисперсия, т.е. вариация в ряду у за счет всех остальных факторов, кроме х

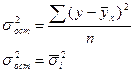
Из правила сложения дисперсий

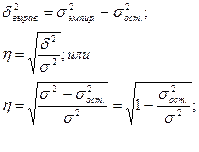
Корреляционное отношение, находится в пределах от 0 до 1.

1. Если результ. полностью зависит от фактора х

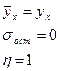
2. Фактор х не анализ. влияние на у

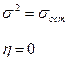
Т.е. чем ближе значение корреляционного отношения к 1, тем больше связь у и х. Чем ближе к 0, тем связь слабее. Обычно η меньше 0,3, зависимость маленькая; 0,3-0,6 – зависимость средняя, больше 0,6 – большая.

Пример.

внесено удобр.,ц/га. х	урож.,ц/га у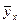
		6,2
		8,5
		10,4
		11,9
		13,0
Итого:15

Зависимость параболическая.

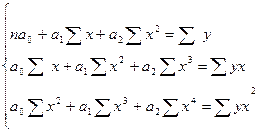
5a₀+15a₁+55a₂=50

15a₀+55a₁+225a₂=167

55a₀+225a₁+979a₂=649

a₀=3,14

a₁=2,98

a₂=-0,241

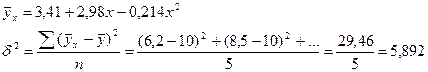
Дисперсия ряда теоретическая. Значение результативного признака.

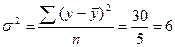Дисперсия ряда эмпирическая. Значение результативного признака.

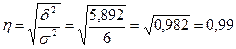
Корреляционное отношение характеризует высокую степень тесноты зависимости изменения урожайности от количества внесенных удобрений.

От теоретического следует отличать эмпирическое корреляционное отношение, которое рассчитывается по данным групповых таблиц.

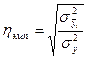
где 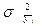- дисперсия групповых средних результативного признака

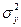- общая дисперсия результативного признака.

Эмпирическое корреляционное отношение не требует знания и расчета уравнений регрессии, а основывается на сопоставлении межгрупповой и общей дисперсий результативного признака, рассчитанных по групповым таблицам.

Рассмотрим пример с корреляционной таблицей:

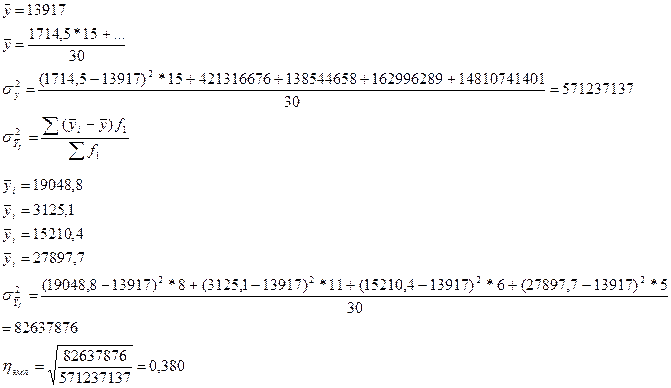На основе этого показателя можно сделать вывод о том, что вариация групповых средних несущественно зависит от вариации группировочного признака.