Оценка надежности коэффициента корреляции и коэффициента регрессии

Коэффициент корреляции можно рассчитать и по выборочным данным. В этом случае должна быть рассчитана ошибка коэффициента корреляции μ_r.

Если n > 50, то этот показатель определяется по формуле 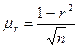, а сам коэффициент корреляции – в пределах r±3μ_r.

Если n<50 или значение коэффициента корреляции невелико, то приходится решать вопрос о том, насколько реальна связь между у и х. Это можно определить сопоставляя между собой численные значения r и μ_r.

1. Если 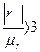, то r считается значимым, а связь реальной.

2. Если 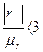, то связь между у и х недоказана, то можно высказать предположение, что значение коэффициента корреляции, отличное от 0, получено случайно.

Аналогично определяется и ошибка корреляционного отношения и его значимость. Необходимо отметить, что при различных значениях отобранных единиц в выборочную совокупность, параметры уравнения регрессии также различны.

Следовательно, в каждом конкретном случае, найдя по эмпирическим данным параметры уравнения регрессии, необходимо определить их возможные ошибки и пределы, в которых эти параметры могут находиться, а также определить значимость (существенность) этих параметров.

Рассмотрим .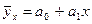

Средняя ошибка (μ) параметра а₀ рассчитывается по формуле:

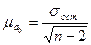
где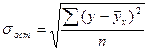

(n-2) – число степеней свободы.

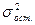можно найти из правила сложения дисперсий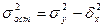

Разделим обе части уравнения на общую дисперсию

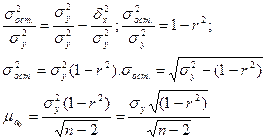
Средняя ошибка параметра а₁

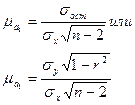
Зная среднюю ошибку параметра и задавшись определенной вероятностью, а следовательно, и коэффициентом доверия (t), можно построить, для каждого параметра доверительные интервалы.

Для коэффициента регрессии: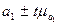

Значимость (существенность) коэффициента регрессии проверяется путем сопоставления самого параметра (а₁), с его средней ошибкой

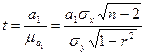
По значению t в зависимости от объема наблюдений следят о значимости параметра.

Для n>20, если t>3, параметры считаются значимыми.

Для n<20, то обращаются к таблице значений критерия t Стьюдента.

Если t_факт.<t_табл., то параметры считаются значимыми.

Для а₁=2,12 средняя ошибка будет равна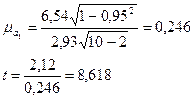

При уровне значимости d=0,05, k=10-2=8, t_табл.=2,306

Т.к. фактически t>табличного, то можно сделать вывод о значимости коэффициента регрессии а₁.