Методы корреляционно-регрессионного анализа связи показателей
Наиболее разработанная – метод парной корреляции, рассматривающая влияние вариации факторного признака (х) на результативный (у).
Для выявления связи применяются различные виды уравнения прямолинейной и криволинейной связей. Аналитическая связь между ними может быть описана следующими уравнениями:
Прямая 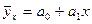
Гипербола 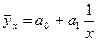
Парабола 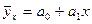 +а2х2
+а2х2
Определить тип уравнения можно, исследуя зависимость графически. Однако есть более общее указание.
- если результативный и факторный признаки ↑ одинаково, примерно в арифметической прогрессии – прямая.
- при обратной – гиперболическая.
- если факторный признак увеличивается в арифметической, а результативный быстрее, то парабола или степенная.
Оценка параметров уравнений регрессии а0; а1; а2 осуществляется методом наименьших квадратов
при линейной зависимости
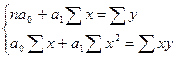
n – объем исследуемой совокупности.
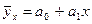 ; где а0 – усредненное влияние на результативный признак случайных факторов. а1 – коэффициент регрессии показывает насколько изменяется в среднем значение результативного признака при увеличении факторного на единицу собственного измерения.
; где а0 – усредненное влияние на результативный признак случайных факторов. а1 – коэффициент регрессии показывает насколько изменяется в среднем значение результативного признака при увеличении факторного на единицу собственного измерения.
Пример:
Имеются данные, характеризующие деловую активность ЗАО:
прибыль (тыс.р.) и затраты на 1 р. произведенной продукции (коп.)
| № | затраты на 1 р. произв. продукции (коп.) | прибыль (тыс.р.) | х2 | ху | 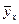
|
| Итого: |
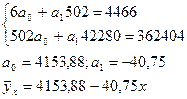
На практике часто исследования проводятся по большому числу наблюдений. В этом случае исходные данные представляют в сводной корреляционной таблице. При этом анализу подвергаются сгруппированные данные и по факторному х и по результативному у, т.е. уравнение парной регрессии целесообразно строить на основе сгруппированных данных.
Если значения х и у заданы в определенных интервалах (а-в), то для каждого интервала сначала определяют середину интервала (а+в)/2, а затем уже коррелируют значения х/ и у/ и строят уравнения регрессии между ними.
Корреляционная таблица дает общее представление о направлении связи. Если оба признака (х и у) располагаются в возрастающем порядке, а частоты (fxy) сосредоточены по диагонали сверху вниз направо.

прямая обратная
О тесноте связи между признаками х и у по корреляционной таблице можно судить по кучности расположения частот вокруг диагонали (поскольку заполненные клетки таблицы в стороне от нее).
Если клетки заполнены большими цифрами, то связь слабая. Чем ближе частоты (fxy) располагаются к одной из диагоналей, тем теснее связь. Если в расположении частот (fxy) нет системности, то можно судить об отсутствии связи.
Пример:
| величина капитала, тыс.р. у | величина работающих активов, тыс.р. х | Число банков fy | уfy | xyfy | |||||
| 14-70 | 70-126 | 126-182 | 182-238 | ||||||
| у/ср | х/ср | ||||||||
| 145-2684 | 1714,5 | 25717,5 | |||||||
| 2684-4624 | 3654,0 | ||||||||
| 4624-6564 | |||||||||
| 6564-8503 | 7533,5 | ||||||||
| 8503-125842 | 67172,5 | 335862,5 | |||||||
| Число предпр. fx | |||||||||
| xfx | |||||||||
| x2fx | |||||||||
Если у нас наличие линейной связи:
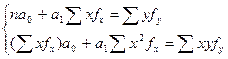
где n=30 коммерческих банков.
fx и fy – число банков согласно распределению соответственно по факторному и результативному признакам.
yfy; xfx – значение результативного и факторного признаков по конкретной группе коммерческих банков.
Для 1 группы yfy= 1714,5*15=25717,5
xfx=42*8=336
хyfy=1714,5*4*42+1714,5*6*98+1714,5*2*154+1714,5*3*210=2904363
х2fx=42*42*8=14112
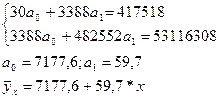
Статистические данные обладают ошибками упрощения, которые возникают как следствие:
1. Неполноты охвата единиц совокупности
2. Неполноты факторов, определяющих явление
3. Характера выбранного уравнения связи
Использование метода наименьших квадратов позволяет получить достоверные оценки при небольшом количестве наблюдений.
При изучении корреляционной связи показателей коммерческой деятельности в условиях наблюдения так называемого малого и среднего бизнеса, анализу подвергается сравнительно небольшие по составу единиц совокупности.
Дата добавления: 2015-09-11; просмотров: 601;
