Понятие корреляции
Все явления в мире взаимосвязаны. Это значит, что каждое событие оказывает влияние на все события, следующие за ним, а само происходит вследствие всех событий, случившихся до него.
До сих пор рассматривались основные статистические характеристики изолированно друг от друга, теперь будем изучать, как и в к5акой форме одно явление оказывает влияние на другое. Это является предметом корреляционно-регрессионного анализа.
Три основные задачи корреляционно-регрессионного анализа:
1. Определение факторов, которые оказывают определяющее воздействие на результативный признак.
2. Определение форм воздействия факторов и результата.
3. Определение степени влияния на результат учтенных и неучтенных факторов.
В статистике изучаются следующие виды связей:
1. Балансовая связь – характеризует зависимость между источниками формирования результатов и их использованием.
2. Компонентные связи – характеризуются тем, что изменение статистического показателя определяется изменением компонентов, входящих в этот показатель, как множители.
Ipq=Ip*Iq
3. Факторные связи – характеризуются тем, что они появляются в согласованной вариации изучаемых показателей.
Одни выступают как факторные, другие как результативные.
При функциональной связи изменение результативного признака обусловлено всецело действием одного факторного признака х, т.е. одному факторному соответствует одно и только одно значение результативного признака y=f(x). Функциональная связь проявляется во всех случаях наблюдения и для каждой конкретной единицы изучаемой величины.
Если причинная зависимость проявляется не в каждом отдельном случае, а в общем, в среднем при большом числе наблюдений, то такая зависимость называется стохастической. Частным случаем стохастической связи является корреляционная, при которой изменение среднего значения результатов признака обусловлено изменением факторных признаков. По степени тесноты связи различают количественные критерии оценки тесноты связи.
| Величина коэффициента корреляции | Характер связи |
| до |±0,3| | практически отсутствует |
| |±0,3|-|±0,5| | слабая |
| |±0,5|-|±0,7| | умеренная |
| |±0,7|-|±1,0| | сильная |
По направлению выделяют связь прямую, т.е. с увеличением или уменьшением значения факторного признака происходит увеличение или уменьшение результата.
Например, увеличение производительности труда способствует увеличению уровня рентабельности.
И обратную, когда значения результативного признака изменяются под воздействием факторного, но в противоположном направлении.
Например, с увеличением фондоотдачи снижается себестоимость единицы продукции.
По аналитическому выражению выделяют связи прямолинейные и нелинейные.
В статистике не всегда требуются количественные оценки, важно просто определить форму воздействия одних факторов на другие.
Для выявления наличия связи, и характера, и направления используются следующие методы:
- приведение параллельных данных
- аналитических группировок
- графический
- корреляции
1.Метод приведения параллельных данных - основан на сопоставлении двух или нескольких рядов статистических величин. Такое сопоставление позволяет установить наличие связи и получить представление о ее характере.
| x | |||||||||
| y |
Т.е. с увеличением x ↑ y, т.е. это может быть либо кривая, либо парабола 2 порядка.
2.Графически - взаимосвязь двух признаков изображается с помощью поля корреляции. В системе координат на оси абсцисс откладываются значения факторного признака, а у – результативного.
При отсутствии тесных связей имеет место беспорядочное расположение точки на графике. Чем сильнее связь между признаками, тем теснее будут группироваться точки вокруг определенной линии, выражающей форму связи.

Для социально-экономических явлений характерно, что наряду с существенными факторами, формирующими уровень результативного признака на него оказывают воздействие многие случайные факторы. Поэтому корреляционная связь отражается функцией у=ψ(х)+ε, где ε – влияние случайных факторов.
3.Корреляция – это статистическая зависимость между случайными величинами, не имеющими строго функционального характера, при котором изменение одной из случайных величин приводит к уменьшению математического ожидания другой. В статистике принято различать следующие варианты зависимостей:
1. Парная корреляция – связь между двумя признаками.
2. Частная корреляция – зависимость между результатом и одним факторным признаком при фиксированном значении других факторных признаков.
3. Множественная корреляция – зависимость результативного и двух или более факторных признаков, включенных в исследование.
Корреляционный анализ имеет своей задачей кол-но определить тесноту связи между двумя признаками (при парной связи) и между результативными и множеством факторных признаков (при многофакторной связи).
Теснота связи количественно выражается величиной коэффициентов корреляции. Величина коэффициентов корреляции служит также оценкой соответствия уравнения регрессии выявленным причинно-следственным связям. Одновременно с корреляцией начала использоваться регрессия. Корреляция и регрессия тесно связаны между собой:
Первая оценивает силу статистической связи, вторая исследует ее форму. Та и другая служат для установления соотношения между явлениями.
Корреляционно-регрессионный анализ как общее понятие, включает в себя измерение тесноты направления связей и установления аналитического выражения (формы) связей (регрессионный анализ).
Регрессионный анализ заключается в определении аналитического выражения связи, в котором изменение одной величины (результативный признак) обусловлено влиянием одной или нескольких независимых величин (факторов), а множество всех прочих факторов, также оказывающих влияние на зависимую величину, принимается за постоянные и средние значения. Регрессия может быть однофакторной (парной).
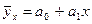 - линейная функция и многофакторной (множественной)
- линейная функция и многофакторной (множественной)
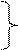
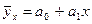 +а2х2 - парабола
+а2х2 - парабола
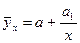 - гипербола нелинейная регрессия
- гипербола нелинейная регрессия
По направлению связи распределяют:
а) прямую регрессию (положительную)
б) обратную (отрицательную), т.е. с увеличением или уменьшением независимой величины зависимая соответственно уменьшается или увеличивается.
Прямая (положительная) регрессия

Обратная (отрицательная) регрессия

Дата добавления: 2015-09-11; просмотров: 604;
