Интерпретация коэффициентов корреляции
Причинность и корреляция
Наличие корреляции двух переменных отнюдь не означает,что между ними существует причинная связь. Несмотря на то, что сосуществование (корреляцию) событий можно использовать для выявления причинных связей наряду с другими методологическими подходами, монопольное применение корреляции к анализу причинности рискованно и может вводить в заблуждение. Во-первых, даже в тех случаях, когда можно предположить существование причинной связи между двумя переменными, которые коррелированны,  сам по себе ничего не говорит о том, вызывает ли Х появление Y или Y вызывает появление Х. Во-вторых, часто наблюдаемая связь существует благодаря другим переменным, а не двум рассматриваемым. В-третьих, взаимосвязи переменных в педагогике и общественных науках почти всегда слишком сложны, чтобы их объяснением могла служить единственная причина. Успеваемость в школе – результат многочисленных влияний, да и сама по себе она является сложным понятием, которое нельзя описать адекватно при помощи какого бы то ни было одного измерения.
сам по себе ничего не говорит о том, вызывает ли Х появление Y или Y вызывает появление Х. Во-вторых, часто наблюдаемая связь существует благодаря другим переменным, а не двум рассматриваемым. В-третьих, взаимосвязи переменных в педагогике и общественных науках почти всегда слишком сложны, чтобы их объяснением могла служить единственная причина. Успеваемость в школе – результат многочисленных влияний, да и сама по себе она является сложным понятием, которое нельзя описать адекватно при помощи какого бы то ни было одного измерения.
Мы рассмотрим некоторые проблемы, возникающие при попытке выявить причинные связи с помощью корреляции. Вероятно, справедливо, что в США существует положительная корреляция между средним заработком преподавателей в школах и процентом выпускников, поступивших в колледж. Значит ли это, что высокооплачиваемое школьное преподавание вызывает появление лучше подготовленных абитуриентов колледжа? Увеличится ли процент выпускников, поступивших в колледж, если повысить плату преподавателям?
Установлено, что процент «исключенных» из школ отрицательно коррелирует с числом учебников, приходящихся на ученика в библиотеках этих школ. Но здравый смысл подсказывает нам, что нагромождение книг в библиотеке не больше повлияет на число исключенных, чем наем ленивого служащего на магическое увеличение школьной библиотеки. Если бы только здравый смысл всегда служил нам так хорошо!
Многие исследователи не останавливаются на том ложном выводе, что корреляция свидетельствует на первый взгляд о причинной зависимости, а выводят также и другое заключение. Они приписывают причинной связи определенное направление. Рассмотрим более внимательно правдоподобный пример. Предположим, что в большой группе учащихся коэффициент корреляции между тревожностью (Х) и результатом теста IQ (Y) равен – 0,60. Означает ли это, что большое волнение привело к тому, что учащиеся плохо выдержали испытание, а более спокойные ученики, не травмированные страхом, оказались в состоянии успешно проявить свои способности? Этот вывод склонны делать некоторые исследователи. Но разве не столь же правдоподобно считать, что сам этот тест есть фактор, вызывающий беспокойство? Не могли ли тупые ученики бояться испытания их интеллекта, а способные найти эксперимент приятным и не вызывающим беспокойства? В данном случае вопрос в том, можно ли сказать, что X вызывает Y или что Y вызывает X? Обычный коэффициент корреляции между X и Υ не может дать ответ на этот вопрос. Без экспериментальной проверки связи сами по себе часто трудно интерпретировать. Искусный экспериментальный подход к той же самой задаче предполагал бы формирование группы тревожных учеников и сравнение их оценок с оценками контрольной группы.
Идентичные группы с различными средними
Существенная корреляция между двумя переменными – это факт, который в разных ситуациях можно объяснить по-разному. Некоторые корреляции – результат измерения причины и ее действия, например, когда X – пища, съеденная за месяц, а Y – вес, приобретенный за то же время. Другие корреляции возникают при измерениях двух переменных с общей причиной или влиянием, например, когда X – успеваемость по английскому языку, a Y – по общественным наукам. Иногда возникают иные корреляции, когда объединяются две различные группы, в каждой из которых X и Υ не имеют связи.
Предположим, что девочки проявляют большую тревожность, чем мальчики, при проверке, например, по шкале выраженной тревожности Тейлора. Хорошо известно, что девочки, как правило, имеют более высокие оценки по английскому языку по сравнению с мальчиками, особенно в средних классах. Диаграмма рассеивания тревоги и успеваемости по английскому языку для 13 мальчиков и 14 девочек могла быть подобна той, которая представлена на рис. 7.3.
На рис. 7.3 видна довольно сильная положительная связь между тревогой и успехами в английском, когда объединяются оценки мальчиков и девочек. Свидетельствует ли это о том, что тревожность (напряжение) заставляет учащегося усерднее трудиться и тем самым стимулирует большие достижения? Вовсе нет. Если бы это было так, то почему никому не удалось установить какую-либо связь между двумя переменными отдельно для мальчиков и девочек?
На рис. 7.3 видно, что ненулевые корреляции могут получиться в тех случаях, когда объединяются отдельные группы, например мальчики и девочки с различными средними. В результате такого объединения могут наблюдаться либо положительные, либо отрицательные связи.

Рис. 7.3 – Диаграмма рассеивания оценок тревоги и успеваемости
по английскому языку для 13 мальчиков (М) и 14 девочек (Д)
Идентификация подгрупп с различными средними по X и Υ не исключает возможности корреляции X и Υ. Однако она допускает более рациональное объяснение того, почему rxy существенно отличается от нуля.
Нелинейность и формы маргинальных распределений переменных
Из всех способов, которыми могут быть связаны измерения двух переменных, rxy оценивает только один. Величина rxy представляет собой меру степени линейной связи X и Y. Если X и Υ жестко линейно связаны, то точки диаграммы рассеивания будут расположены на одной прямой, как это показано в табл. 7.4. Если мы разбросаем точки на таком графике над и под прямой случайным образом и приблизительно на одинаковые расстояния, то получим различные степени линейных в своей основе связей между X и Y. Если точки на диаграмме рассеивания ориентируются – хотя и отклоняются случайным образом – относительно кривой, связь X и Y может быть существенно криволинейной. Из того, что rxy измеряет только линейную связь между X и Y, следует, что различные виды нелинейных связей X и Y могут дать такие значения rxy, которые подозрительно близки к нулю, если интерпретировать их без учета диаграммы рассеивания. Если известно, что X и Υ в общем тесно связаны линейно, то смысл rxy совершенно ясен. Однако если X и Υ имеют некую нелинейную связь, то близкие к нулю значения rxy могут быть получены даже несмотря на то, что X и Υ сильно связаны. Рис. 7.4 содержит две разные диаграммы рассеивания, каждая из которых имеет близкие к нулю коэффициенты корреляции.
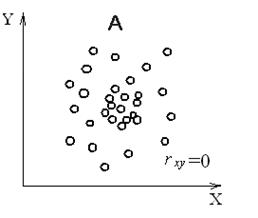
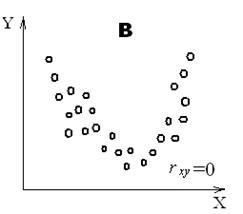
Случайная связь Сильная нелинейная связь
Рис. 7.4 – Два примера близкой к нулю корреляции, определяемой произведением моментов
Хотя обе диаграммы рассеивания А и В на рис. 7.4 имеют нулевые коэффициенты корреляции, в В есть существенная связь между Х и Υ, а в А нет никакой систематической связи между ними. Одной иллюстрации на рис. 7.4, по-видимому, достаточно для предупреждения против опрометчивого вывода о том, что две переменные не связаны только потому, что rxy = 0. Оценки педагогических и психологических тестов часто дают «потолочные» или «подвальные» эффекты у нетипичных групп, то есть испытания могут быть слишком легкими или слишком трудными, ибо многие получают максимальную или минимальную оценку. Диаграмма рассеивания оценок теста А, который характеризуется «потолочным эффектом», и теста В с «подвальным эффектом» могла бы быть подобна диаграмме рис. 7.5.
Величина rАВ для данных рис. 7.5 невелика; вероятно, она приблизительно равна 0,30. Оказывается, что в области, для которой оба теста эквивалентны по трудности, они связаны более сильно. Считают, что если бы тест А был более трудным, а тест В – более легким без радикального изменения их содержания, то величина rАВ увеличилась бы. Диаграмма рассеивания для подобных измененных тестов, возможно, обладала бы меньшей нелинейностью, чем имеющаяся. (Этот пример показывает другой важный момент: степень связи между любыми двумя переменными – независимо от того, как эта связь выражена, – зависит от характера измерения переменных. Например, мы обычно считаем, что характеристики веса и роста довольно сильно связаны между собой у взрослых людей; но нетрудно представить себе весьма плохие способы измерения этих переменных – например, измерение с помощью субъективных суждений четырехлетних детей, оценки веса и роста которых не показали бы почти никакой корреляции).
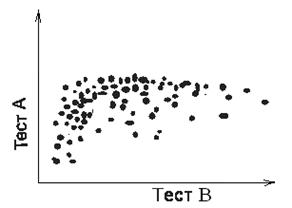
Рис. 7.5 – Диаграмма рассеивания оценок для теста А (слишком простого) и теста В (слишком трудного для испытываемой группы)
Дополнительные замечания об интерпретации rxy
Пределы [от –1 до +1] и выражения [«сильно связанный», «умеренно связанный», «не связанный»] непосредственно относятся к определенным статистическим моделям. Две наиболее часто применяемые модели – нормальная двумерная поверхность (см. лекцию 6) и модель линейной регрессии (см. лекцию 8). Для вычисления коэффициента Пирсона не требуется никаких предположений, но интерпретация его смысла определенно зависит от области, в пределах которой данные приводятся в соответствие с подходящей статистической моделью для выполнения этой интерпретации. Поскольку реальные данные отклоняются от модели, под которую их подгоняют (например, двумерной нормальной поверхности), то пределы коэффициента корреляции могут сужаться, а предлагаемая интерпретация терять смысл.
В качестве примера того, как максимальное значение rxy может ограничиваться величиной менее +1, когда частотные распределения X и Y асимметричны (скошены) в различных направлениях, рассмотрим 99 оценок X и Y со следующими распределениями частот:
| Оценка для X: | |||||||||||
| Частота: | |||||||||||
| Оценка для Y: | |||||||||||
| Частота: |
Χ скошен сильно положительно, а Y – сильно отрицательно. Максимальная возможная величина rxy приблизительно 0,60. Другими словами, даже если между X и Y существует максимально возможная линейная связь, rxy будет только 0,60. Это вовсе не говорит о слабости rxy как описательной меры; нельзя упрекать в нарушении тех функций, которые не предусматривались. Тот факт, что rxy не может превышать 0,60 в данном примере, надо рассматривать скорее как утешительный. Когда X имеет так много значений ниже среднего, а Y характеризуется множеством значений, превышающих среднее, то невозможно, чтобы все положительные отклонения Yi относительно 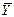 были связаны с положительными отклонениями Xi относительно
были связаны с положительными отклонениями Xi относительно 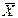 . На самом деле rxy не может достигнуть крайних значений +1 или –1, пока распределения X и Y не имеют идентичной формы.
. На самом деле rxy не может достигнуть крайних значений +1 или –1, пока распределения X и Y не имеют идентичной формы.
Эта зависимость максимальной величины rху от распределений Х и Y создает известные трудности. Предположим, что получено rху = 0,60. Что это характеризует? Умеренную связь двух переменных, совместное распределение частот которых подобно двумерной нормальной поверхности, или максимально возможную связь между положительно скошенным X и отрицательно скошенным Y? Ранее мы видели, как подобные сомнения касались нулевого значения rху. Действительно ли X и Y не связаны или связь между ними нелинейная? Наиболее удовлетворительное разрешение всех этих сомнений достигается анализом диаграммы рассеивания значений X и Y. На такой диаграмме можно сразу увидеть, имеют ли X и Υ выраженную криволинейную связь и значительно ли они скошены.
Дата добавления: 2015-09-21; просмотров: 2301;
