Параметрически заданные функции
Связь между аргументом и функцией может быть записана через дополнительную переменную, называемую параметром, то есть в виде системы, в которой прописывается зависимость аргумента от параметра и зависимость функции от того же параметра:
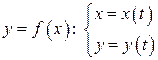 , где
, где 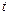 – это параметр,
– это параметр, 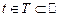 .
.
В этом случае функция 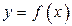 называется функцией, заданной параметрически.
называется функцией, заданной параметрически.
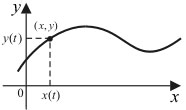 Рис. 41
Рис. 41
| при этом сама траектория движения может описываться уравнением 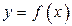 или или 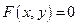 , т. е. задавать функцию , т. е. задавать функцию  или или 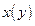 . .
|
Например, в механике при описании движения точки по некоторой траектории 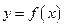 задаются абсцисса и ордината движущейся точки как функции времени t, (рис. 41).
задаются абсцисса и ордината движущейся точки как функции времени t, (рис. 41).
От параметрически заданной функции можно перейти к явной или неявной форме её задания, если удаётся исключить параметр t.
Пример (параметрически заданные функции)
1. 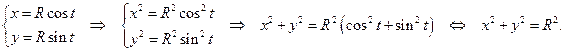
Таким образом, система 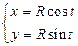 — это есть параметрические уравнения окружности радиуса R с центром в начале координати, следовательно, задают две функции
— это есть параметрические уравнения окружности радиуса R с центром в начале координати, следовательно, задают две функции 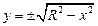 ,
, 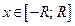 :
:
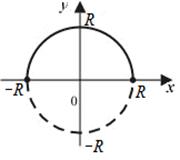
| на верхней полуокружности
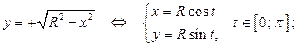 на нижней полуокружности
на нижней полуокружности
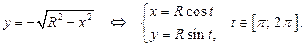
|
2. 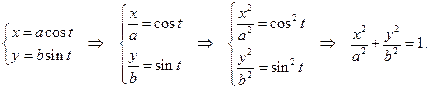
Таким образом, система 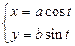 — это есть параметрические уравнения эллипса с полуосями a и b и с центром в начале координат, они задают две функции:
— это есть параметрические уравнения эллипса с полуосями a и b и с центром в начале координат, они задают две функции:

| на верхней половине эллипса
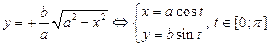 ;
на нижней половине эллипса ;
на нижней половине эллипса
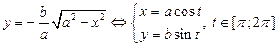 . .
|
3. 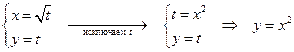 — уравнение параболы;
— уравнение параболы;
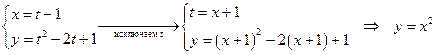 — —
| уравнение той же параболы. |
Из последнего примера хорошо видно, что для одной и той же функции можно записать несколько вариантов параметрических уравнений, вводя по-разному параметр.
Выполнить исключение параметра из системы параметрических уравнений не всегда возможно, поэтому нужно уметь работать и с функциями, имеющими только параметрические задания.
Дата добавления: 2015-10-19; просмотров: 8322;
