Условия Коши-Римана
Бернхард Риман (1826–1866) — немецкий математик.
Рассмотрим функцию комплексной переменной 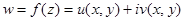 , определенную на некоторой области и имеющую в какой – либо точке этой области производную
, определенную на некоторой области и имеющую в какой – либо точке этой области производную
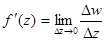
Стремление к нулю Dz®0 может осуществляться в следующих случаях:
1) 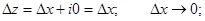
2) 
В первом случае:
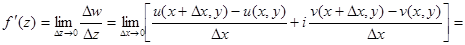
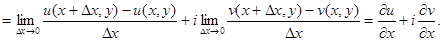
Во втором случае:
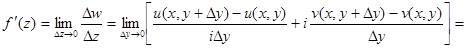
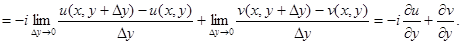
Тогда должны выполняться равенства:
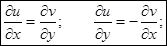
Эти равенства называются условиями Коши – Римана, хотя еще раньше они были получены Эйлером и Даламбером.
Теорема. Если функция 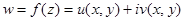 имеет производную в точке
имеет производную в точке
z = x + iy, то ее действительные компоненты u и v имеют в точке (х, у) частные производные первого порядка, удовлетворяющие условию Коши-Римана.
Также справедлива и обратная теорема.
На основании этих теорем можно сделать вывод, что из существования производной следует непрерывность функции.
Теорема. Для того, чтобы функция 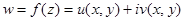 была аналитической на некоторой области необходимо и достаточно, чтобы частные производные первого прядка функций u и v были непрерывны на этой области и выполнялись условия Коши – Римана.
была аналитической на некоторой области необходимо и достаточно, чтобы частные производные первого прядка функций u и v были непрерывны на этой области и выполнялись условия Коши – Римана.
Интегрирование функций комплексной переменной.
Пусть 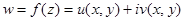 - непрерывная функция комплексного переменного z, определенная в некоторой области и L – кривая, лежащая в этой области.
- непрерывная функция комплексного переменного z, определенная в некоторой области и L – кривая, лежащая в этой области.
 у
у
В
L
А
х
Кривая L задана уравнением 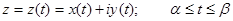
Определение. Интегралот функции f(z) вдоль кривой L определяется следующим образом:

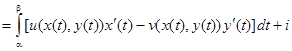
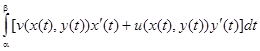
Если учесть, что 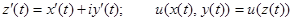 , то
, то
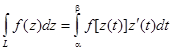
Теорема. (Теорема Коши) Если f(z) - аналитическая функция на некоторой области, то интеграл от f(z) по любому кусочно – гладкому контуру, принадлежащему этой области равен нулю.
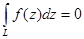
Дата добавления: 2015-10-13; просмотров: 684;
