Теорема о вычетах
Теорема. Пусть функция f(z) – аналитическая на всей плоскости z, за исключением конечного числа точек z1, z2, …, zN. Тогда верно равенство:
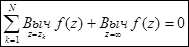
А интеграл от функции по контуру L, содержащему внутри себя эти точки, равен
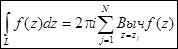
Эти свойства применяются для вычисления интегралов. Если функция f(z) аналитическая в верхней полуплоскости, включая действительную ось, за исключением N точек, то справедлива формула
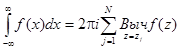
Пример. Вычислить определенный интеграл 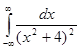 .
.
Подынтегральная функция является аналитической в верхней полуплоскости за исключением точки 2i. Эта точка является полюсом второго порядка.
Найдем вычет функции 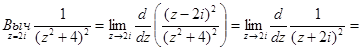
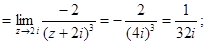
Получаем 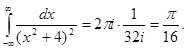
Пример. Вычислить определенный интеграл 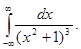
Подынтегральная функция является аналитической в верхней полуплоскости за исключением точки i. Эта точка является полюсом второго порядка.
Найдем вычет функции
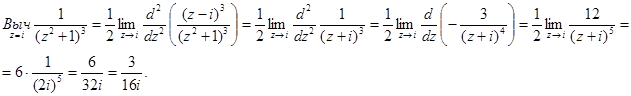
Получаем 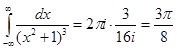
Дата добавления: 2015-10-13; просмотров: 622;
