Производная функций комплексного переменного
Определение. Производной от однозначной функции w = f(z) в точке z называется предел:
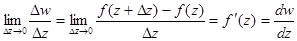
Определение. Функция f(z), имеющая непрерывную производную в любой точке области D называется аналитической функцией на этой области.
Правила дифференцирования функций комплексного аргумента не отличаются от правил дифференцирования функций действительной переменной.
Аналогично определяются производные основных функций таких как синус, косинус, тангенс и котангенс, степенная функция и т.д.
Производные гиперболических функций определяются по формулам:

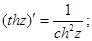
Вывод правил интегрирования, значений производных основных функций ничем не отличается от аналогичных операций с функциями действительного аргумента, поэтому подробно рассматривать их не будем.
Дата добавления: 2015-10-13; просмотров: 725;
