Преобразование Фурье. Определение. Если f(x) – любая абсолютно интегрируемая на всей числовой оси функция, непрерывная или имеющая конечное число точек разрыва первого рода на
Определение. Если f(x) – любая абсолютно интегрируемая на всей числовой оси функция, непрерывная или имеющая конечное число точек разрыва первого рода на каждом отрезке, то функция
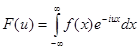
называется преобразованием Фурье функции f(x).
Функция F(u) называется также спектральной характеристикой функции f(x).
Если f(x) – функция, представимая интегралом Фурье, то можно записать:
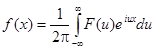
Это равенство называется обратным преобразованием Фурье
Интегралы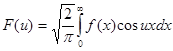 
и 
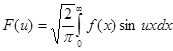называются соответственно косинус - преобразование Фурье и синус – преобразование Фурье.
Косинус – преобразование Фурье будет преобразованием Фурье для четных функций, синус – преобразование – для нечетных.
Преобразование Фурье применяется в функциональном анализе, гармоническом анализе, операционном исчислении, теории линейных систем и др.
Дата добавления: 2015-10-13; просмотров: 592;