Достаточные признаки разложимости в ряд Фурье

Теорема. (Теорема Дирихле) Если функция f(x) имеет период 2p и на отрезке

[-p;p] непрерывна или имеет конечное число точек разрыва первого рода, и отрезок

[-p;p] можно разбить на конечное число отрезков так, что внутри каждого из них функция f(x) монотонна, то ряд Фурье для функции f(x) сходится при всех значениях х, причем в точках непрерывности функции f(x) его сумма равна f(x), а в точках разрыва его сумма равна 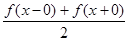, т.е. среднему арифметическому предельных значений слева и справа. При этом ряд Фурье функции f(x) сходится равномерно на любом отрезке, который принадлежит интервалу непрерывности функции f(x).

Функция f(x), для которой выполняются условия теоремы Дирихле называется кусочно-монотонной на отрезке [-p;p].

Теорема. Если функция f(x) имеет период 2p, кроме того, f(x) и ее производная f’(x) – непрерывные функции на отрезке [-p;p] или имеют конечное число точек разрыва первого рода на этом отрезке, то ряд Фурье функции f(x) сходится при всех значениях х, причем в точках непрерывности его сумма равна f(x), а в точках разрыва она равна 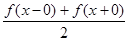. При этом ряд Фурье функции f(x) сходится равномерно на любом отрезке, который принадлежит интервалу непрерывности функции f(x).

Функция, удовлетворяющая условиям этой теоремы, называется кусочно – гладкойна отрезке [-p;p].

Разложение в ряд Фурье непериодической функции.

Задача разложения непериодической функции в ряд Фурье в принципе не отличается от разложения в ряд Фурье периодической функции.

Допустим, функция f(x) задана на отрезке [a, b] и является на этом отрезке кусочно-монотонной. Рассмотрим произвольную периодическую кусочно-монотонную функцию f₁(x) c периодом 2Т ³ ïb-aï, совпадающую с функцией f(x) на отрезке [a, b].

y

f(x)

a - 2T a a b a+2T a + 4T x

Таким образом, функция f(x) была дополнена. Теперь функция f₁(x) разлагается в ряд Фурье. Сумма этого ряда во всех точках отрезка [a, b] совпадает с функцией f(x), т.е. можно считать, что функция f(x) разложена в ряд Фурье на отрезке [a, b].

Таким образом, если функция f(x) задана на отрезке, равном 2p ничем не отличается от разложения в ряд периодической функции. Если же отрезок, на котором задана функция, меньше, чем 2p, то функция продолжается на интервал (b, a + 2p) так, что условия разложимости в ряд Фурье сохранялись.

Вообще говоря, в этом случае продолжение заданной функции на отрезок (интервал) длиной 2p может быть произведено бесконечным количеством способов, поэтому суммы получившихся рядов будут различны, но они будут совпадать с заданной функцией f(x) на отрезке [a,b].