Ряд Фурье для четных и нечетных функций

Отметим следующие свойства четных и нечетных функций:

1)

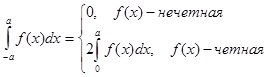
2) Произведение двух четных и нечетных функций является четной функцией.

3) Произведение четной и нечетной функций – нечетная функция.

Справедливость этих свойств может быть легко доказана исходя из определения четности и нечетности функций.

Если f(x) – четная периодическая функция с периодом 2p, удовлетворяющая условиям разложимости в ряд Фурье, то можно записать:

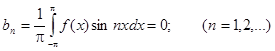
Таким образом, для четной функции ряд Фурье записывается:

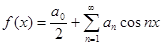
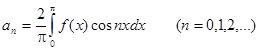
Аналогично получаем разложение в ряд Фурье для нечетной функции:

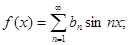
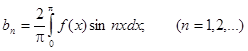
Пример. Разложить в ряд Фурье периодическую функцию 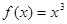с периодом T = 2p на отрезке [-p;p].

Заданная функция является нечетной, следовательно, коэффициенты Фурье ищем в виде:

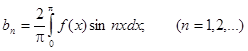
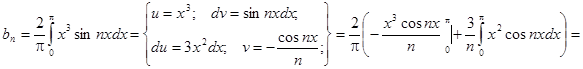
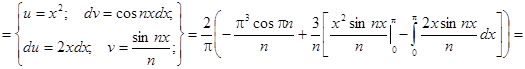
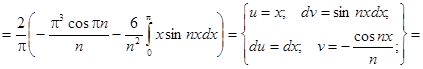
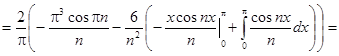
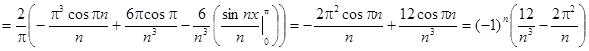
Получаем:

.

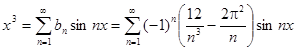Построим графики заданной функции и ее разложения в ряд Фурье, ограничившись первыми четырьмя членами ряда.