Разложение голоморфной функции в ряд Лорана.
Теорема. Если функция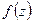 
голоморфна в 
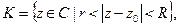то её можно разложить в этом кольце в ряд Лорана.
|
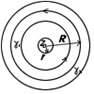
И проведём 2 окружности (меньшую обозначим 
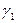(радиуса 
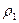); большую 
(радиуса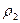 
)). 
по построению. Пусть точка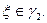 
Рассмотрим ядро Коши: 
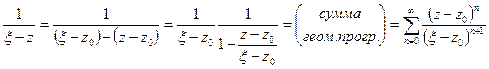Оценим равномерную сходимость: 
оценка не зависит от 
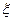и меньше 1, следовательно
ряд сходится равномерно по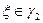 
(по признаку сравнения), следовательно его можно
интегрировать почленно:
.
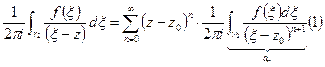Пусть 
. Рассмотрим ядро Коши: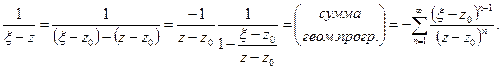 
Оценим члены этого ряда: 
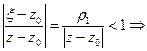аналогично ряд сходится равномерно по 
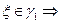интегрируем почленно: 
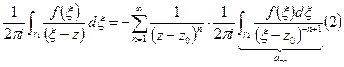. Из (1) вычтем (2): 
по формуле Коши. 
ИЗОЛИРОВАННЫЕ ОСОБЫЕ ТОЧКИ
Дата добавления: 2015-09-02; просмотров: 787;