Ряд Лорана в окрестности изолированной особой точки.

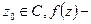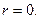голоморфна в - пример кольца с радиусом По теореме:

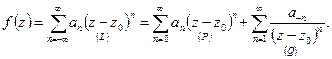(L) – ряд Лорана в .

Определение. Ряд (Р) называется правильной частью ряда Лорана. Ряд (Q) называется главной частью ряда Лорана.

Рассмотрим 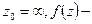голоморфна в 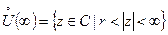- частный случай кольца с радиусом 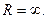По теореме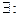 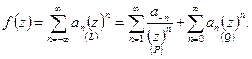(L) – ряд Лорана в 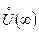. (Р) – правильная часть ряда Лорана (состоит из слагаемых, ограниченных при 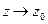). (Q) – главная часть ряда Лорана (состоит из слагаемых, неограниченных при ).

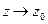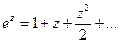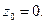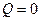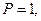Пример. 1) Указать главную, правильную части в окрестности точки Тогда всё это – правильная часть. А главная часть . Если рассматривать в окрестности точки то а .

Теорема. Пусть 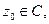(конечна) пусть 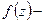голоморфна в . Пусть - главная часть ряда Лорана в . Тогда справедливы следующие утверждения:

1) устранимая особая точка функции 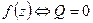все коэффициенты нулевые.

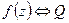2) полюс функции содержит конечное ненулевое число отличных от нуля слагаемых.

3) существенная особая точка функции 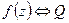содержит много ненулевых слагаемых.

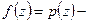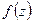Доказательство. Докажем 1): Напишем ряд Лорана в точке . степенной ряд, сходящийся в окрестности точки к функции - голоморфной в этой окрестности 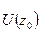(в частности непрерывной). Тогда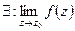

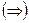Дано устранимая особая точка . Доопределим функцию 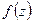в точке по непрерывности, тогда 1. функция 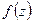- голоморфна в 2. функция 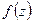- непрерывна в 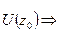по теореме об устранимой особенности функция 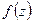- голоморфна в 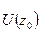(если функция голоморфна в круге, то она раскладывается в степенной ряд), то 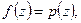а 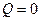(из единственности разложения в ряд Лорана).

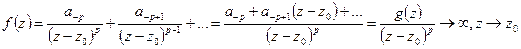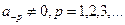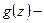Докажем 2): Дано . Мы считаем , и голоморфна в точке и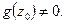

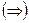
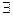предел: 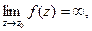рассмотрим функцию 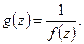Т.к. предел = бесконечности, то в некоторой окрестности 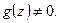Таким образом, 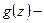голоморфна в некоторой проколотой окрестности точки .

Чему равен: 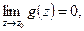таким образом - устранимая особая точка. Доопределив её по непрерывности, получаем функцию голоморфную в некоторой окрестности точки , разложим её в ряд Тейлора, тогда

Определение. Номер р называется порядком нуля для функции .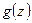

Теперь: 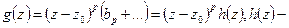голоморфная в точке и 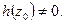Вернёмся к функции 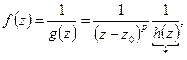* - голоморфна в некоторой окрестности точки 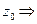можем разложить в степенной ряд. Получим: 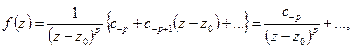а это ряд Лорана, где Q содержит конечное число слагаемых.

Утверждение 3) – следствие из 1) и 2) (исключением этих случаев).