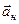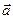Кинематика и динамика вращательного движения твердого тела

1. Физика – наука о наиболее общих свойствах и формах движения материи. Закономерности, открытые физикой, легли в основу множества прикладных наук, разрабатывающих новые технологии и определяющих научно-технический прогресс.

Материю мы воспринимаем в виде вещества и в виде поля, которые при определенных условиях могут превращаться друг в друга.

Различают три уровня организации материи в виде вещества, каждый уровень изучается с помощью определенных физических принципов:

- мегамиры; структурные единицы мегамиров – галактики, состоящие из звезд, планет и других образований (в нашей галактике 10 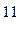звезд); объекты мегамиров имеют громадные массы и размеры (масса небольшой звезды – Солнца составляет 10 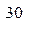кг, радиус – 696 тыс. км), определяющим фактором для них служит гравитация, закономерности мегамиров изучаются с помощью теории относительности;

- макромир – это мир окружающих нас предметов, его описывает классическая физика;

- микромир – это своеобразный мир молекул, атомов и элементарных частиц; для его изучения разработана квантовая механика.

Человеческий опыт позволил накопить, прежде всего разнообразные сведения о предметном макромире, в результате научного обобщения этого опыта сформировался раздел физики «Механика».

Кинематика изучает движение тел без учета причин движения. При рассмотрении движения тел удобным оказалось представлять тела в виде материальных точек. Материальной точкой называют тело, размерами которого можно пренебречь в условиях данной задачи (учитывается только масса тела). Любое тело можно считать материальной точкой, если его размеры малы по сравнению с расстоянием, на которое тело перемещается, или с расстоянием до других тел.

Движение – это изменение положения тела относительно других тел и для описания движения необходимо ввести систему отсчета. Система отсчета – это система координат, начало которой связано с телом отсчета, и часы для отсчета времени. Так с помощью декартовой системы координат можно определить координаты тела x,y,z в любой момент времени.

Траектория – геометрическая линия, описываемая материальной точкой (телом) при своем движении (прямолинейная, круговая, эллиптическая и т.д.). Путь S измеряется в метрах, это расстояние, пройденное телом вдоль своей траектории. Перемещением 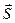называют направленный отрезок, соединяющий начальную и конечную точку пути.

Основные характеристики движения – скорость и ускорение.

Скоростью называется физическая величина, численно равная пути, пройденному телом за единицу времени. Если тело за отрезок времени Δt прошло путь ΔS, то его средняя скорость на этом пути равна vср= ΔS/ Δt. Точное значение скорости в данный момент времени получим, если отрезок времени возьмем бесконечно малым. Мгновенная скорость

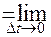
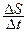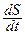
v = (1.1)

Скорость имеет направление, это векторная величина. При Δt→0 путь и перемещение совпадают, поэтому

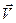
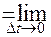
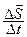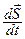= , (1.2) (1.2)

Вектор скорости направлен по касательной к траектории в любой ее точке.

Единица измерения скорости, т.е. размерность [v]=[S] / [t], т.е. [v]= м/с.

Ускорением называют физическую величину, численно равную изменению скорости в единицу времени. Мгновенное ускорение

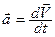(1.3)

Размерность ускорения [a]=[V]/ [t], т.е. [а]= м/с².

Скорость может изменяться по величине и по направлению, поэтому ввели нормальное ускорение 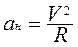, которое характеризует изменение скорости по направлению, и тангенциальное ускорение 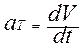, которое характеризует изменение скорости по величине (рис.1.1).

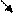
Рис.1.1.

Нормальное ускорение направлено к центру кривизны траектории в любой ее точке. При прямолинейном движении радиус траектории стремится к бесконечности и нормальное ускорение равно нулю. Тангенциальное ускорение направлено по касательной к траектории в любой ее точке. При равномерном движении тангенциальное ускорение равно нулю.

Полное ускорение 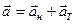. Величина полного ускорения определяется из соотношения .

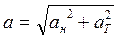2. В основе классической механики лежат три закона Ньютона. Динамика изучает движение и его причины. Основным законом динамики стал второй закон Ньютона: ускорение тела пропорционально действующей на тело силе и обратно пропорционально массе тела; направлено ускорение в сторону действия силы

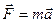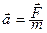или (1.4)

Масса тела измеряется в килограммах (кг) и служит мерой инертности тела. Инертность – это способность тела сохранять состояние покоя или движения.

Сила – мера действия на тело другого тела. Единица измерения силы [F]=[m]·[a], т.е. [F]= кг·м/с² = Н (ньютон).

Если на тело действует несколько сил, то их можно заменить одной силой, которая называется равнодействующей и определяется по правилу векторного сложения сил. В этом случае ускорение пропорционально равнодействующей силе и направлено в сторону ее действия.

Обычно на любое тело действует сила тяжести F=mg, где g=9,8 м/с² - ускорение свободного падения тела. При движении возникает сила трения

Fтр = kFдавл, где Fдавл – сила нормального давления тела на плоскость движения. На горизонтальном пути Fтр = kmg.

Силы, действующие на тело, могут уравновешивать друг друга, тогда

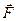равн = 0. Условие равновесия сил: сумма проекций всех сил на каждую из трех взаимно перпендикулярных осей должна быть равна нулю.

Если 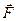равн=0, то , значит . Так как m≠0, то 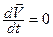, а значит 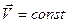. Отсюда вытекает первый закон Ньютона: если на тело не действуют другие тела или действие тел взаимно компенсировано, то тело покоится или движется равномерно и прямолинейно (по инерции). Первый закон Ньютона выполняется в инерциальных системах отсчета, то есть в таких системах, которые движутся друг относительно друга равномерно и прямолинейно.

Третий закон Ньютона: любые два тела действуют друг на друга с силами, равными по величине и противоположными по направлению

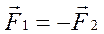(1.5)

В классической механике состояние частицы или системы частиц в любой момент времени можно полностью описать координатами и скоростью. Зная закон движения (основной закон динамики) частицы, можно предсказать и определить положение частицы в любой момент времени.

Следует различать понятия «масса тела» и «вес тела». Массу тела определяют с помощью рычажных весов, сравнивая ее с эталоном массы.

Вес тела – это сила, с которой тело давит на опору или растягивает подвес. Если тело и опора относительно друг друга покоятся, вес тела равен его силе тяжести. При движении вверх с ускорением сила давления на опору растет и превышает силу тяжести. При движении вниз с ускорением вес тела меньше силы тяжести, а при свободном падении наступает невесомость.

3.Импульсом тела называют произведение массы тела на его скорость

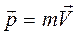(1.6)

Основной закон динамики 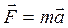можно представить как 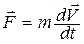. Так как в классической механике 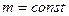, то 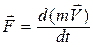, то есть 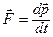. Основной закон динамики можно записать также в ви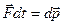де , где 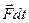- импульс силы.

Замкнутой называют систему тел, которые взаимодействуют между собой и не взаимодействуют с окружающими систему телами. Пусть замкнутая система состоит из двух тел. При их взаимодействии выполняется третий закон Ньютона 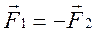, то есть 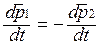. Преобразуя, получим 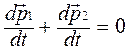, а значит 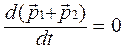. Это выполняется, если 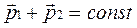. Можно показать, что этот вывод верен для замкнутых систем, состоящих из любого количества тел, в этом случае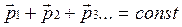

Закон сохранения импульса: полный импульс тел замкнутой системы остается постоянным.

Закон сохранения импульса используется в реактивном движении. Он является причиной отдачи при резких бросках тел, выстреле орудий и т.п.

Импульс системы тел можно представить в виде произведения суммарной массы частиц на скорость центра масс системы .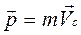

Центром масс системы называется точка, имеющая координаты

; ; .

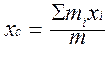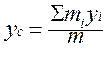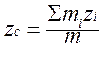Скорость центра масс системы

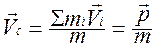, (1.7)

где 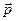- импульс системы, а 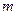- суммарная масса.

Лекция 2

Тема:Кинематика и динамика вращательного движения твердого тела

Вопросы:1) Кинематика вращательного движения.

2) Основной закон динамики вращательного движения.

3) Момент импульса. Закон сохранения момента импульса.

1.Влюбом сложном движении можно выделить два основных вида движения – поступательное и вращательное. Движение поступательное, если любая прямая, проведенная в теле, остается при движении параллельной самой себе. При вращательном движении частицы тела описывают окружности вокруг некоторого общего центра.

Пусть частица вращается вокруг не проходящей через нее оси (рис.2.1).

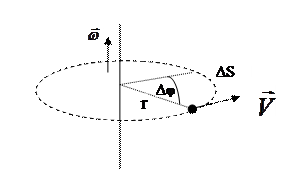Рис.2.1

Угловой скоростью называется физическая величина ω, численно равная углу, на который повернулась частица за единицу времени

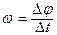(2.1)

Мгновенное значение угловой скорости 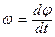. Размерность [ω]= рад/с. Частица может иметь два направления вращения - по часовой стрелке и против, поэтому угловой скорости также приписывают два направления вдоль оси вращения.

Угловая ω и линейная V скорости связаны между собой. За время Δt частица проходит путь ΔЅ (рис.2.1). ΔЅ = rΔφ, разделим на Δt и получим

V = r ω.

На практике используют такие характеристики вращательного движения как:

частота ν – число оборотов за единицу времени;

период Т – время одного полного оборота.

Соотношения, связывающие угловую скорость и частоту ω = 2πν, угловую скорость и период ω = 2π/Т, часто применяются для решения различных задач.

Угловым ускорением называется физическая величина, численно равная изменению угловой скорости за единицу времени

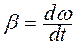(2.2)

Для равнопеременного вращательного движения .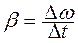

Размерность углового ускорения [β]= рад/с².

Вектор углового ускорения также направлен вдоль оси вращения и совпадает по направлению с вектором .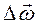

2.Рассмотрим твердое тело, вращающееся вокруг проходящей через него оси под действием силы F (рис.2.2). Твердым называется тело, которое не деформируется при движении, то есть расстояния между его частицами не меняются.

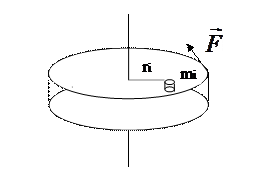
Рис.2.2

Мысленно разобьем тело на малые массы m1, m2, m3…mi…., которые можно считать материальными точками (по сравнению с расстоянием ri до оси вращения их размер мал). Применим для каждой частицы второй закон Ньютона: 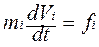, где fi – сила, действующая на частицу.

Умножим обе части равенства на ri и заменим Vi = ri ω. Получим

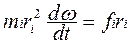
Просуммируем полученное равенство по всем частицам тела

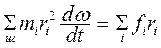(2.3)

Правая часть равенства представляет собой полный момент М внешних сил.

Моментом силы относительно некоторой оси вращения называется произведение силы F на плечо силы d. Плечом силы называется кратчайшее расстояние (перпендикуляр) от оси вращения до линии действия силы.

Моментом инерции материальной точки относительно некоторой оси вращения называется произведение массы точки на квадрат расстояния ее до оси вращения: I = mr². Момент инерции тела относительно некоторой оси вращения равен сумме моментов инерции всех частиц тела относительно этой оси вращения.

Проведя замену в уравнении 2.3, получим основной закон динамики вращательного движения твердого тела:

Iβ = M (2.4)

Момент внешних сил, вращающих тело вокруг данной оси, равен произведению момента инерции тела относительно этой оси на угловое ускорение тела.

Момент инерции тела – это мера инертности тела при вращательном движении. У тела может быть множество моментов инерции, так как телу можно задать множество осей вращения.

Моменты инерции некоторых тел относительно оси, проходящей через центр тела перпендикулярно к плоскости диска, кольца или основания цилиндра:

а) кольцо, полый тонкостенный цилиндр I = mR²;

б) диск, сплошной цилиндр I = 1/2mR²;

в) шар I = 2/5mR².

Для определения момента инерции тела относительно оси, не проходящей через тело, можно применить теорему Штейнера: момент инерции тела относительно произвольной оси равен сумме момента инерции тела I0 относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния α между осями

I = I0 + mα². (2.5)

3.Моментом импульсаматериальной точки называют произведение импульса материальной точки на ее расстояние до оси вращения

l = mVr.

Момент импульса твердого тела относительно некоторой оси вращения равен сумме моментов импульса всех его частиц относительно этой оси вращения: L = 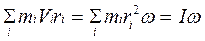. Вектор момента импульса тела (вращательного момента) совпадает по направлению с вектором угловой скорости .

Основной закон динамики вращательного движения тела 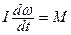можно представить, как 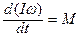,так как момент инерции от времени не зависит. В замкнутой системе результирующий момент внешних сил отсутствует, значит 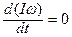. Отсюда следует, что Iω = const. Для системы тел замкнутой системы выполняется I1ω1 + I2ω2 + I3ω3 +….= const.

Закон сохранения момента импульса: в замкнутой системе полный вращательный момент входящих в эту систему тел остается постоянным. У свободно вращающегося тела остается постоянной как величина момента импульса, так и направление оси вращения в пространстве. Это используют в гироскопе.

Лекция 3

Тема:Работа и энергия

Вопросы:1) Работа постоянной и переменной силы.

2) Энергия. Потенциальная энергия.

3) Кинетическая энергия. Закон сохранения энергии.

1. При неупругом столкновении тела могут остановиться, в этом случае исчезает механическое движение и тела нагреваются. Законы динамики такого превращения объяснить не могут, потребовалось ввести новую физическую величину – «энергию». В механике передача энергии осуществляется путем совершения работы.

Пусть тело перемещается на некоторое расстояние S под действием постоянной силы F. Опытным путем получена формула работы

A = FScosα, (3.1)

где α - угол между направлением силы и перемещения. Единица измерения работы [A] = [F][S] = Н·м = Дж (джоуль).

Если 0 ≤α< 90°, то cosα > 0 и А > 0, то есть работа внешней силы над телом положительна (сила действует в направлении движения).

Если α = 90°, то cosα = 0 и А = 0 , значит сила, перпендикулярная к направлению движения, работу над телом не совершает.

Если 90°<α ≤180°, то cosα

Мощностью называют физическую величину, численно равную работе, совершаемой телом, за единицу времени: N = A/t. Единица измерения мощности [N]= Дж/с = Вт (ватт).

Рассмотрим перемещение тела из точки 1 в точку 2 под действием непостоянной силы F≠const. Может меняться как величина, так и направление силы. Работу на всем пути уже нельзя определять выражением 3.1. Мысленно разобьем путь на участки ΔЅ1, ΔЅ2, ΔЅ3,… ΔЅi…, такие, чтобы силу в пределах отдельного участка можно было считать постоянной. Тогда работу на каждом участке можно определить как ΔAi = FiΔSicosαi., а работу на всем пути сложением .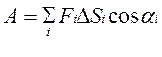

Чем меньше длина участков, тем точнее результат определения работы, поэтому работу на всем пути следует определять как

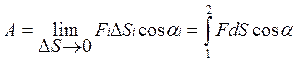(3.2)

Под знаком интеграла стоит элементарная работа dA = FdScosα на бесконечно малом отрезке пути dS.

2. Энергия – это количественная мера движения материи во всех формах ее движения. Различают механическую энергию (кинетическую и потенциальную), тепловую, электрическую, ядерную и др. Для всех видов энергии единой мерой является джоуль.

Если тело деформируется под действием силы, то сила совершает работу. Моделью упругого тела служит пружина. Чтобы пружину растянуть, надо приложить силу F, равную и противоположно направленную силе противодействия пружины Fупр = - kx, где k – коэффициент упругости (жесткость) пружины, а х – величина деформации пружины. Значит F = kx, т.е. F≠const. Работа деформации

А = 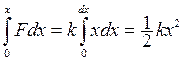(3.3)

Работа внешней силы идет на увеличение запаса энергии деформируемого тела, значит потенциальная энергия деформируемого тела Епот = А, т.е.

(3.4)

Рассмотрим тело, поднятое над поверхностью Земли на высоту h. На тело действует сила тяготения, направленная к центру Земли, следовательно, надо совершить работу, равную силе тяжести, чтобы поднять тело.

Работа А = mgh и идет на увеличение запаса потенциальной энергии тела в поле Земли Епот = mgh. Уменьшая свою высоту, тело совершает работу, равную mgh, или отдаст энергию mgh.

Потенциальная энергия – это энергия взаимодействия тел или частей тела, зависящая от их взаимного расположения. Потенциальная энергия появляется всегда, когда между телами или частями тела действуют силы, зависящие от расстояния между телами.

3.Кинетической энергией тела называют энергию его движения. Она равна работе, совершаемой внешней силой F, которая выводит тело из состояния покоя и сообщает ему скорость V.

Действие силы подчиняется основному закону динамики .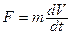

После умножения на dS получим 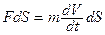и проведем замену переменных: FdS = dA; V = 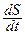. Получим dA = mVdV. Проинтегрируем обе части равенства:

.

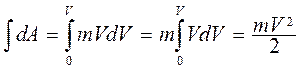Работа пошла на сообщение кинетической энергии А = Екин., значит

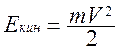(3.5)

Если надо увеличить скорость, то следует совершить работу А = ΔЕ, т.е. 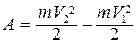. Если движущееся тело остановилось, то оно передало свою энергию телу, с которым оно взаимодействовало при торможении.

При вращении тела его частицы обладают кинетической энергией 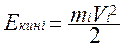, скорости частиц могут иметь разные значения. Кинетическая энергия вращающегося тела:

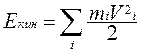; так как Vi = riω, то .

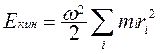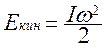(3.6)

Если тело движется поступательно и одновременно вращается, то его кинетическая энергия равна сумме кинетической энергии поступательного и вращательного движений.

В изолированной от внешних воздействий системе выполняется закон сохранения энергии: полная энергия остается постоянной при любых ее превращениях.

Закон сохранения механической энергии Епот + Екин = const выполняется, если в системе отсутствует трение и неупругие деформации. При их наличии часть механической энергии превращается в тепло.

Лекция 4

Тема:Механика жидкостей и газов

Вопросы:1) Гидростатическое давление. Закон Паскаля. Закон

Архимеда

2) Стационарное течение. Условие неразрывности струи.

3) Уравнение Бернулли.

4) Внутреннее трение в жидкостях.

5) Движение тел в жидкостях и газах

1. В отличие от твердых тел жидкости и газы не сохраняют свою форму, а всегда принимают форму сосуда, в котором находятся. Однако они обладают упругостью и в состоянии равновесия давят на ограничивающую их поверхность.

Давление на данном участке поверхности – это отношение силы, действующей на данный участок, к площади этого участка 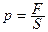. Единица измерения давления [p]= Н/м² = Па (паскаль).

В жидкостях и газах давление передается во все стороны и силы давления перпендикулярны к ограничивающей поверхности при любой ее ориентации (рис.4.1).

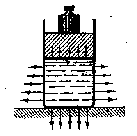
Рис.4.1

Силы давления, создаваемые гирей, равномерно распределены по поверхности соприкосновения, однако на нижнюю часть сосуда дополнительно давит сила тяжести самой жидкости.

В 17 веке Блез Паскаль установил, что при действии лишь поверхностных сил давление во всех точках внутри жидкости одинаково. Это можно показать теоретически с помощью рис.4.2.

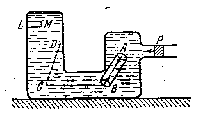
Рис.4.2

Выделим мысленно внутри жидкости цилиндр с осью АВ. Выделенный объем находится в покое, хотя на него тоже действуют силы давления со стороны остальной жидкости (создаются воздействием поршня). Для равновесия необходимо, чтобы силы давления на основания цилиндра были равны, значит давления в точках А и В одинаковые. Таким же образом можно рассмотреть точки В и С, С и D и показать, что во всех этих точках давление одинаково.

Закон Паскаля позволяет объяснить действие гидравлического пресса (рис.4.3)

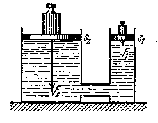
Рис.4.3

Гидравлический пресс состоит из двух цилиндров разного диаметра, соединенных трубкой и снабженных поршнями. Пространство под поршнями заполняется жидкостью. Пусть к малому поршню приложена сила F1 , определим, какую силу F2 надо приложить ко второму поршню, чтобы сохранить равновесие. Можно в данном случае пренебречь давлением силы тяжести жидкости. Давление под первым поршнем 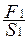, давление под вторым поршнем 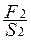. Эти давления должны быть одинаковы: 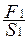= 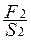, значит

,

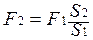т.е. сила F2 во столько раз больше силы F1, во сколько раз площадь второго поршня больше площади первого. Таким образом, при помощи гидравлического пресса малой силой можно уравновесить большую силу.

Рассмотрим теперь равновесие жидкости под действием вилы тяжести самой жидкости.

В открытом сосуде на поверхность действует атмосферное давление, одинаковое на всей открытой поверхности. Это поверхность равного давления, поэтому она находится на одном уровне (поверхность уровня). В сообщающихся сосудах все свободные поверхности принадлежат одной и той же поверхности уровня, поэтому находятся в одной плоскости (на одной высоте) (рис.4.4).

Рис.4.4

В глубине жидкости давление растет, т.к. к атмосферному давлению добавляется сила тяжести жидкости. Выделим мысленно тонкий вертикальный цилиндр в жидкости (рис.4.5) и рассмотрим условия его равновесия.

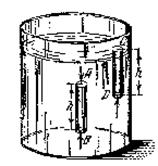
Рис.4.5

Равнодействующая сил, действующих на боковую поверхность цилиндра, равна нулю. Вдоль вертикали действуют три силы: сила давления на верхнее основание, равная pАS и направленная вниз, сила давления на верхнее основание, равная pВS и направленная вверх, а также сила тяжести жидкости в объеме цилиндра mg, направленная вниз. Массу жидкости в объеме цилиндра можно представить как m = ρV = ρSh, где ρ – плотность жидкости, а V – объем цилиндра.

Условие равновесия: pАS + ρgSh = pВS. Отсюда получается pВ – pА = ρgh. На поверхности жидкости давление столба жидкости равно нулю. Таким образом, гидростатическое давление на глубине h равно

p = ρgh.

Распределение давления по глубине зависит только от плотности жидкости и расстояния от верхнего уровня жидкости, но не зависит от формы сосуда (рис.4.6).

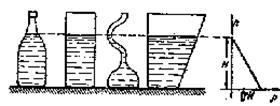
Рис.4.6

Из условия равновесия жидкости следует, что на тело, погруженное в жидкость, снизу действует большая сила давления, чем сверху. Этим объясняется плавание тел.

Рассмотрим в жидкости тело, имеющее форму параллелепипеда (рис.4.7). Силы, действующие на боковые грани, взаимно компенсируются. Силы, действующие на верхнее и нижнее основания равны соответственно

F1 = p1S = ρghS; F2 = p2S = ρg(h + H)S

Равнодействующая этих сил направлена вверх и равна

F = F2 – F1 = ρg(h + H)S – ρghS = ρgHS,

где HS = V объем тела, а ρ – плотность жидкости.

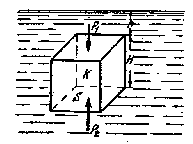
Рис.4.7

В результате получаем, что на тело действует направленная вверх сила F = ρg V.

Закон Архимеда: на тело, погруженное в жидкость, действует выталкивающая сила, равная силе тяжести вытесненной этим телом жидкости.

Выталкивающая сила зависит от плотности жидкости. Так, в соленой воде плавать легче, чем в пресной. Если плотность тела больше, чем плотность жидкости, то тело тонет и наоборот, тела с меньшей плотностью выталкиваются на поверхность.

2. Рассматривая движение жидкостей и газов, мы не учитываем их атомного строения, т.е. вещество рассматривается как сплошная среда. Жидкости и газы сами не имеют определенной формы и принимают форму того сосуда, который заполняют. В отличие от газов, жидкости обладают малой сжимаемостью, однако в потоках газов изменениями их объема часто можно пренебречь и законы движения потоков жидкостей и газов оказываются одинаковыми. Рассмотрим эти законы на примере потоков жидкостей.

Жидкости, в которых отсутствуют силы трения, называются идеальными. Движение идеальной жидкости можно описать скоростью, с которой частицы жидкости проходят через каждую точку пространства, с помощью линий тока.

Линии тока – это такие линии, проведенные в движущейся жидкости, касательные к которым в каждой точке совпадают с направлением вектора скорости частиц жидкости в этих точках (рис.4.8).

Рис.4.8

Густота линий тока, т.е. число линий, пересекающих перпендикулярную к ним единичную площадку, принимается пропорциональной величине скорости жидкости в данной точке. Поэтому картина линий тока позволяет судить как о направлении, так и о величине вектора скорости в разных точках потока жидкости.

Если картина линий тока остается неизменной во времени, то течение жидкости установившееся или стационарное. Стационарным называется такое течение, при котором любая частица жидкости проходит данную точку пространства с одинаковым значением скорости. Линии тока при установившемся течении совпадают с траекториями частиц.

Стационарное течение газа или воды по трубам, каналам и рекам представляет собой довольно сложную картину. Анализ стационарного потока упрощается, если мысленно разбить текущую жидкость на тонкие трубки тока. Такая трубка тока образована поверхностью, проведенной через несколько линий тока, т.е. ее стенки образованы траекториями частиц.

Рассмотрим трубку тока переменного сечения (рис.4.9).

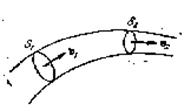
Рис.4.9

Обозначим площади поперечного сечения на концах трубки тока S1 и S2 (площадки S1 и S2 перпендикулярны к направлению движения потока). Через любое сечение за единицу времени в стационарном потоке проходит одинаковый объем жидкости, значит V1 = V2. За время Δt через S1 пройдут все частицы, находящиеся в момент начала отсчета времени на расстоянии v1 Δt, значит пройдет объем V1 = S1v1Δt. Через сечение S2 пройдет объем жидкости V2 = S2v2Δt. Из равенства этих объемов следует: S1v1Δt = S2v2Δt, т.е.

S1v1 = S2v2 =const.

Условие неразрывности струи: произведение скорости частиц на площадь поперечного сечения в любом месте потока имеет одинаковое значение. Значит, там, где поток сужается, скорость жидкости увеличивается, а в местах расширения потока скорость уменьшается (рис.4.10).

Рис.4.10

3. Изменение скорости частиц жидкости может быть вызвано только изменением давления вдоль потока. В широкой части давление возрастает, впереди давление больше и жидкость тормозится.

Выделим в потоке трубку тока переменного сечения, концы ее находятся на разной высоте от уровня, который принимается за нулевой (рис.4.11).

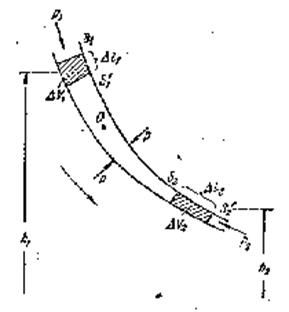
Рис.4.11

Выделим в жидкости малый объем ΔV1 на высоте h1. Через промежуток времени Δt выделенный объем ΔV2 окажется на высоте h2. Из-за неразрывности струи ΔV1 = ΔV2 = ΔV. Масса выделенного объема равна

m = ρΔV, где ρ – плотность жидкости (плотностью называется масса единицы объема вещества, кг/м³).

В начальный момент времени полная энергия выделенного объема жидкости равна Е1 = Екин + Епот ; 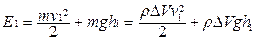. Через время Δt полная энергия выделенного объема станет равной 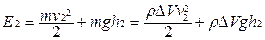. Работа сил давления, приложенного к сечениям S1 и S2 равна A = p1 S1 Δl1 – p2 S2 Δl2 = (p1 – p2) ΔV. Изменение энергии идет на совершение этой работы:

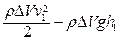- = (p1 – p2) ΔV.

Это выражение можно сократить на ΔV и после переноса получим

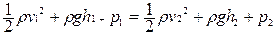, т.е в установившемся потоке вдоль линии тока величины скорости, высоты и давления связаны соотношением, которое носит название уравнения Бернулли: .

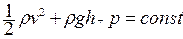Здесь 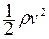- динамическое давление в потоке, 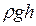- весовое давление, р –статическое давление. Если рассмотреть горизонтальный поток переменного сечения, то в нем будет отсутствовать весовое давление и уравнение Бернулли примет вид: 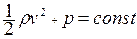. Уравнение показывает, что в тех точках, где скорость жидкости больше, давление меньше и наоборот.

4. В реальных жидкостях всегда присутствует внутреннее трение, на преодоление которого тратится энергия и которое затормаживает движение.

Рассмотрим две горизонтальные пластины в жидкости (рис.4.12), нижняя пластина закреплена с помощью пружины, а верхняя равномерно перемещается под действием внешней силы F, уравновешивающей силу трения.

Рис.4.12

Частицы жидкости, прилипшие к верхней пластине, движутся вместе с ней. В результате хаотического теплового движения часть молекул из этого слоя переходят в соседний слой жидкости и передают ему импульс направленного движения (молекулы соседнего слоя получают движение в том же направлении, но с меньшей скоростью). Так передается движение от слоя к слою и получают импульс частицы, прилипшие к нижней пластине и сама пластина, пружина растягивается. Значит, со стороны жидкости на пластины действует сила трения, которую на основании опыта можно представить формулой:

,

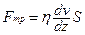где S – площадь пластин, 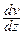- градиент скорости, η – коэффициент внутреннего трения (вязкость) жидкости, зависящий от температуры и природы вещества. У жидкостей вязкость при нагревании уменьшается, а у газов увеличивается.