Кинематика и динамика материальной точки. 4 страница

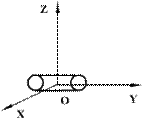
Двухатомные жесткие молекулы, например молекулы водорода, азота и др., обладают пятью степенями свободы: они имеют 3 степени свободы поступательного движения и 2 степени свободы вращения вокруг осей ОХ и OZ (см.рис.). Вращением вокруг оси OY можно пренебречь, т.к. момент инерции ее относительно этой оси пренебрежимо мал. Поэтому вклад энергии вращательного движения вокруг оси OY в суммарную энергию двухатомной молекулы можно не учитывать.

Молекулы, состоящие из трех и более жестко связанных атомов, не лежащих на одной прямой, имеют число степеней свободы i = 6: три степени свободы поступательного движения и 3 степени свободы вращения вокруг осей ОХ, OY и OZ.

В случае, если расстояние между атомами может изменяться (атомы совершают колебания у положения равновесия), появляются дополнительные степени свободы. Согласно молекулярно-кинетической теории газов движение молекул носит беспорядочный характер; эта беспорядочность относится ко всем видам движения молекулы. Ни один из видов движения не имеет преимущества перед другим. При статистическом равновесии движений энергия в среднем распределяется равномерно между всеми видами движения. Закон равномерного распределения энергии по степеням свободы молекул можно сформулировать следующим образом: статистически в среднем на каждую степень свободы молекул приходится одинаковая энергия.

. Поступательное движение молекул характеризуется средней кинетической энергией, равной

Так как поступательному движению соответствует 3 степени свободы, то в среднем на одну степень свободы движения молекул приходится энергия

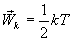
В однородном газе, молекулы которого имеют любое число степеней свободы i, каждая молекула в среднем обладает энергией движения, равной

В теории идеального газа потенциальная энергия взаимодействия молекул считается равной нулю. Поэтому внутренняя энергия идеального газа определяется кинетической энергией хаотического (теплового) движения всех его молекул.

Так как в одном моле любого вещества содержится NА (число Авогадро

) молекул, то внутренняя энергия одного моля газа будет

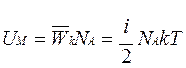
Учитывая, что получим 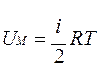, здесь R=8,31 Дж/(моль·К) – универсальная газовая постоянная.

Для любой массы m газа с молярной массой М, т.е. для любого числа молей формула для внутренней энергии имеет вид

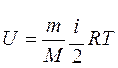
Из этого выражения следует, что внутренняя энергия является однозначной функцией состояния и, следовательно, при совершении системой любого процесса, в результате которого система возвращается в исходное состояние, полное изменение внутренней энергии равно нулю.

4. Беспорядочное тепловое движение молекул, непрерывные столкновения между ними приводят к тому, что молекулы, хотя и сравнительно медленно, перемещаются из одной точки пространства в другую. В результате столкновения изменяются величины и направления скоростей молекул, что приводит к передаче импульса и энергии. По этой причине в газовой среде, если рассматривать бесконечно малые объемы отдельных участков среды, самопроизвольно возникают флуктуации плотности (концентрации), температуры и давления газа, которые мгновенно исчезают. Если данные неоднородности вызваны посторонним источником и носят постоянный характер, то хаотическое движение молекул стремится ликвидировать эти неоднородности. При этом в газе возникают особые процессы, которые носят название явлений переноса. К ним относятся диффузия, теплопроводность и внутреннее трение.

Диффузия. Если в локальном объеме распределена примесь другого газа (или увеличена плотность данного газа), то хаотическое движение молекул будет способствовать выравниванию концентрации газовых молекул. Процесс выравнивания концентрации газовых молекул называется диффузией. Наблюдения показывают, что в процессе диффузии через площадь поверхности 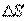, расположенную нормально оси, вдоль которой происходит изменение концентрации вещества за время , переносится масса вещества 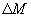, пропорциональная градиенту концентрации 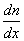, площади 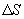и времени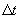

Это уравнение выражает закон Фика. Величина D называется коэффициентом диффузии. Знак минус означает, что масса переносится в сторону убывания концентрации. С точки зрения молекулярно-кинетической теории

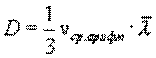
Таким образом, коэффициент диффузии определяется средней длиной свободного пробега 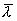и средней арифметической скоростью 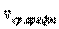молекул.

Теплопроводность. В случае неодинаковых температур в различных частях газа те молекулы, которые находятся в более теплых областях, в среднем обладают большей кинетической энергией, чем молекулы в более холодных областях. И здесь молекулярное движение сопровождается суммарным переносом энергии в направлении более холодных частей газа, вследствие чего происходит выравнивание температуры. Этот процесс называется теплопроводностью. Явление теплопроводности заключается в переносе теплоты 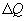от более горячего слоя с температурой 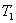к более холодному, температура которого 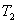, Закон теплопроводности был сформулирован Фурье: теплота 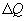переносимая через элемент площади 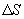за время 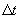, пропорциональна градиенту температуры 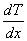, площади 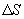и времени :

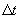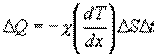
где χ - коэффициент теплопроводности, он зависит от среднеарифметической скорости молекул и плотности газа ( 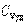- удельная теплоемкость газа):

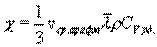
Внутреннее трение. Если два соприкасающихся слоя движутся с различными скоростями, то может происходить выравнивание скоростей слоев газов. В среднем импульсы молекул таких слоев различны - молекулы более быстрых слоев имеют большие значения импульсов. Переход молекул из быстрых слоев в более медленный сопровождается переносом импульса упорядоченного движения. Противоположное по характеру действие оказывают молекулы медленного слоя, перешедшие в быстрый слой, - в этом слое возникают тормозящие силы. Суммарный эффект при этом - выравнивание скоростей слоев. Это явление называется внутренним трением. При этом закон внутреннего трения гласит: сила вязкости F пропорциональна градиенту скорости 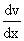и площади S соприкасающихся слоев:

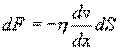
где η - коэффициент внутреннего трения (динамическая вязкость). С точки зрения молекулярно-кинетической теории

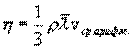
Лекция 8

Тема:Законы термодинамики

Вопросы:1) Первый закон термодинамики

2) Применение первого закона термодинамики к газовым

процессам

3) Второй закон термодинамики

4) Статистический смысл энтропии

5) Круговые процессы. Цикл Карно

1. Термодинамическое состояние тела (например, газа) характеризуется его массой m, молярной массой М, давлением P, объемом V, температурой T. Все эти величины называются термодинамическими параметрами тела. Однако, такие параметры, как P, V, T, имеют смысл только тогда, когда тело находится, хотя бы приближенно, в так называемом состоянии термодинамического равновесия. Так называется состояние, в котором все термодинамические параметры остаются со временем постоянными. Не имеет смысла, например, говорить о температуре газа до тех пор, пока быстрые молекулы у горячей стенки сосуда, вследствие ряда столкновений с другими, не приобретут скоростей порядка средней скорости остальных молекул, иначе говоря, пока система не придет в состояние равновесия. В состоянии т.д.р. для каждого вещества термодинамические параметры связаны между собой уравнением состояния.

Рассмотрим газ, находящийся в цилиндре с поршнем, позволяющем менять объем газа (см. рис).

Цилиндр контактирует с нагревателем, который может сообщать газу тепло. Пусть на поршень оказывается внешнее давление, величина которого может быть любой.

Все процессы, которые будем рассматривать ниже, будут квазистатическими, т.е. медленными настолько, чтобы можно было считать, что в каждый момент газ находится в состоянии т.д.р. Если очень быстро сжать газ, то давление его у поршня окажется на какой-то момент больше, чем в стальном объеме, и тогда нельзя будет говорить о давлении газа вообще. Такой процесс не является квазистатическим. Приближенно квазистатическими являются и процессы, достаточно быстрые с технической точки зрения, например процессы, происходящих в цилиндрах двигателя автомашины во время работы мотора (оказывается, для приближенной квазистатичности требуется, чтобы скорость поршня была мала по сравнению со скоростью звука в газе).

Работа над газом выполняется внешними силами при его сжатии. Работа самого газа выполняется при его расширении. Пусть газ расширяется так, что поршень поднимается на величину dx. Тогда газ выполнит работу dA=Fdx. Так как P=F/S (S – площадь поршня), то получим dA= P S dx = PdV/

Эта величина называется элементарной работой газа. Работа при расширении газа от объема V1 до V2 будет равна

Если по одной оси отложить объем газа, по другой – его давление (плоскость P – V), то работа будет изображаться площадью под кривой P(V) (рис.9.3).

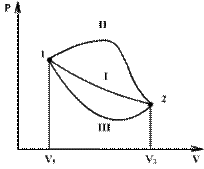
Процесс расширения от объема V₁ до объема V₂ может происходить различным образом: например, можно при этом изолировать газ от нагревателя или, наоборот, нагревать газ и т.д. Иначе говоря, при перемещении из точки 1 в точку 2 в газе могут происходить различные процессы, даже если зафиксировано начальное и конечное состояния. В каждом процессе работа будет иметь свое значение, так как площадь под кривой процесса будет различной (кривые I, II, и III на рис/). Таким образом, выполняемая газом работа зависит от процесса, который с ним происходит.

Работа положительна, если она выполняется газом, и отрицательна, если внешние силы выполняют ее над газом.

Первый закон термодинамики: теплота, сообщаемая системе, расходуется на изменение внутренней энергии системы и на совершение системой работы против внешних сил:

ΔQ=ΔU+ΔA

Первый закон термодинамики представляет собой закон сохранения энергии.

Под внутренней энергией (U) понимается вся энергия системы за исключением механической энергии системы как целого. Сюда входит кинетическая энергия поступательного движения ее молекул, потенциальная энергия их взаимодействия между собой, энергия возбуждения колебаний и вращений молекул, то есть те виды энергии системы, которые могут меняться в термодинамических процессах. Внутренняя энергия идеального газа складывается только из кинетической энергии поступательного и вращательного движения его молекул (взаимодействие молекул незначительно).

В термодинамике для характеристики тепловых свойств тел используется понятие теплоемкости. Теплоемкость тела - количество теплоты необходимое для нагревания тела на один Кельвин

Удельной теплоемкостью называется величина, числено равная теплоте, которую надо сообщить единице массы тела для повышения его температуры на один Кельвин:

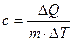
Отсюда можно определить количество теплоты, необходимое для нагревания вещества, массы m: ΔQ = cmΔT

Молярная теплоемкость - количество тепла необходимое для нагревания одного моля вещества на один Кельвин

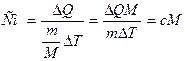
2. Изобарный процесс протекает при постоянном давлении (Р = const), например, при нагревании газа в цилиндре под свободно перемещающимся поршнем.

Из уравнения состояния идеального газа следует, что при р = const, m = const, M = const
V / T = const
Графики, отображающие этот процесс, называют изобарами (см.рис.)

Работа системы при изменении объема от V₁ до V₂ определяется по площади под графиков в координатах P-V

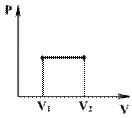
А= Р(V₂ - V₁)

Следовательно, теплота, переданная газу при изобарическом процессе, затрачивается на увеличение его внутренней энергии и совершение работы:

ΔQ=ΔU+ рΔ V

Изохорный процесс протекает при постоянном объеме (V = const), например, при нагревании газа в закрытом сосуде. Из уравнения состояния идеального газа следует, что при V = const, m = const, M = const
Р / T = const
Графики, отображающие этот процесс, называют изохорами (см.рис.).

При изохорическом процессе работа не совершается (площадь под графиком в координатах P-V равна 0).

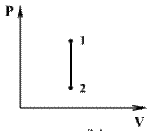
А= рΔ V =0 и первое начало термодинамики приобретает вид: ΔQ=ΔU,

т.е. при изохорическом процессе вся подводимая к газу теплота затрачивается на увеличение внутренней энергии системы.

Изотермический процесс протекает при постоянной температуре ( Т = const). Из уравнения состояния идеального газа следует, что при Т = const, m=const, M = const
P·V = const
Кривые, отображающие этот процесс, называют изотермами (см. рис.)

При изотермическом процессе (Т= const) ΔT=0 и изменение внутренней энергии ΔU=0. Согласно первому закону термодинамики теплота, передаваемая газу, полностью затрачивается на внешнюю работу: ΔQ = ΔA

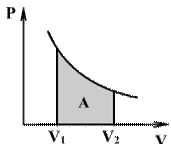
Работа системы численно равны площади под графиком процесса в координатах P-V Аналитическое выражение для работы следующие:

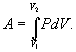
Определим из уравнения Менделеева – Клапейрона Р:

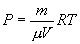
и подставим в уравнение работы

Адиабатический процесс - это такое изменение состояний газа, при котором он не отдает и не поглощает извне теплоты. Следовательно, адиабатический процесс характеризуется отсутствием теплообмена газа с окружающей средой. Адиабатическими можно считать быстро протекающие процессы.

Так как передачи теплоты при адиабатическом процессе не происходит, то ΔQ и уравнение I начала термодинамики принимает вид

ΔU+ΔA = 0 или ΔA = -ΔU. т.е. внешняя работа газа может производиться вследствие изменения его внутренней энергии.

Адиабатное расширение газа (ΔV>0) сопровождается положительной внешней работой, но при этом внутренняя энергия уменьшается и газ охлаждается (ΔT<0).

Сжатие газа (ΔV<0) совершается при воздействии внешних сил; в этом случае работа отрицательна и ΔT>0. Адиабатное сжатие газа сопровождается его нагреванием.

Адиабатический процесс описывается уравнением Пуассона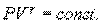

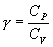
где СV – молярная теплоемкость газа при постоянном объеме

Ср –молярная теплоемкость газа при постоянном давлении, Ср = СV+R.

Линию, изображающую адиабатический процесс в диаграмме состояния, называют адиабатой. На рисунке ниже сплошной линией показан вид адиабаты в (P-V) диаграмме. Для сравнения в том же рисунке пунктирной линией изображена изотерма, соответствующая температуре газа в начальном состоянии. Так как для любого идеального газа показатель адиабаты γ>1 , то в (P-V) диаграмме адиабата всегда идет круче, чем изотерма. Объясняется это тем, что при адиабатическом сжатии увеличение давления обусловлено не только уменьшением объема газа, как при изотермическом сжатии, то также еще и увеличения температуры. При адиабатическом расширении температура газа уменьшается, поэтому давление газа падает быстрее, чем при изотермическом расширении.

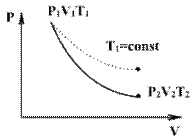
Работа, совершаемая газом в адиабатическом процессе

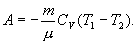
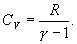
Поэтому

3. Обратимым процессом называют такой процесс, который может быть проведен в обратном направлении таким образом, что система будет проходить через те же состояния, что и при прямом ходе, но в обратной последовательности. После протекания обратимого процесса в одном, а затем в обратном направлении и возвращение системы в первоначальное состояние в окружающих телах не должно оставаться никаких изменений. Например шарик на пружине в вакууме колеблется бесконечно долго.

В том случае, когда после завершения прямого и обратного процессов система вернулась в первоначальное состояние и в окружающей среде остались изменения, процесс является необратимым. Очевидно, что все процессы в природе необратимые.

Выражая всеобщий закон сохранения и превращения энергии, первый закон термодинамики не позволяет определить направление протекания процесса. В самом деле, процесс самопроизвольной передачи энергии в форме теплоты от холодного тела к горячему ни в какой мере не противоречит первому закону термодинамики. Однако при опускании раскаленного куска железа в холодную воду никогда не наблюдается явление дальнейшего нагревания железа за счет соответствующего охлаждения воды. Далее, первый закон не исключает возможности такого процесса, единственным результатом которого было бы превращение теплоты, полученной от нагревателя в эквивалентную ей работу. Так, например основываясь на первом законе можно было бы попытаться построить периодически действующий двигатель, совершающий работу за счет одного источника тепла (например за счет внутренней энергии океана). Такой двигатель называется вечным двигателем второго рода. Обобщение огромного экспериментального материала привело к выводу о невозможности построения вечного двигателя второго рода. Этот вывод получил название второго начала термодинамики.

Существует ряд различных по форме, одинаковых по существу формулировок второго начала. Удобно процессы, протекающие в термодинамических системах, описывать с помощью энтропии. Понятие энтропии S было впервые введено в 1865 году Рудольфом Клаузиусом при рассмотрении работы тепловой машины, однако смысл его был раскрыт позже Больцманом.

Принцип существования энтропии: система может быть переведена из состояния 1 (с параметрами Р1, V1, T1) в состояние 2 (с параметрами Р2, V2, T2) множеством способов, но при этом одинаковым остается изменение энтропии

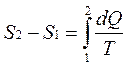
где dQ – количество тепла, полученное системой, а Т – температура системы.

Разность энтропий в двух равновесных состояниях 2 и 1 системы равна приведенному количеству тепла, которое нужно сообщить системе, чтобы перевести ее из состояния 1 в состояние 2.

. В случае обратимого процесса

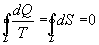
Интеграл по замкнутому контуру - это изменение энтропии во всем цикле, т.е. при обратимых циклах энтропия не меняется: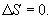

Физический смысл имеет не сама энтропия, а ее изменение. Условно энтропию системы при абсолютном нуле принимают равной нулю. Приближенно изменение энтропии можно представить в виде

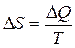
Рассмотрим изолированную систему, состоящую из двух тел с одинаковой теплоемкостью, но с разными температурами (Т2 >Т1).

В системе возникает необратимый процесс теплопроводности. Теплота переходит от нагретого тела 2 к более холодному телу 1. В конце этого процесса температуры станут равными, переход тепла прекратится, система перейдет в состояние термодинамического равновесия. Изменение энтропии первого тела равно 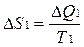, где Т1 –температура первого тела, ΔQ1 – количество теплоты, полученное первым телом. Изменение энтропии второго тела равно 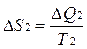, где Т2 –температура второго тела, ΔQ2 – количество теплоты, отданное вторым телом. Так как система изолированная и других тел нет, то ΔQ1 = - ΔQ2.

Общее изменение энтропии системы ΔS = ΔS1 + ΔS2 = - .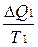

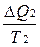Так как Т2 >Т1, то ΔS > 0. Тот же результат получим, если рассмотрим процесс диффузии или необратимые химические реакции.

Второй закон термодинамики: в изолированной системе самопроизвольно могут протекать только те процессы, при которых

происходит увеличение энтропии

Таким образом, энтропия изолированной системы может только возрастать (если в системе протекают необратимые процессы), либо остается постоянной (если в системе протекает обратимый процесс). Убывать энтропия изолированной системы не может. В этом состоит сущность второго закона термодинамики.

В изолированной системе не могут идти процессы, уменьшающие энтропию: теплота не может переходить от холодного тела к более нагретому без дополнительных затрат энергии; газы смешиваются, но не могут сами разделиться и т.д.

4. Смысл понятия энтропии раскрыл Людвиг Больцман с помощью мысленного опыта с молекулами газа.

Пусть в сосуде находятся шесть молекул, которые двигаются хаотически и могут по-разному распределяться в двух половинах сосуда. Распределение 6:0, когда все молекулы собираются в одной половине сосуда реализуется одним способом. Распределение 1:5 реализуется 6 способами (каждая молекула побывает в одной половине сосуда, когда все остальные находятся в другой половине. Распределение 2:4 реализуется 15 способами, распределение 3:3 реализуется 20 способами. Значит, набольшим числом способов реализуется равномерное распределение молекул по объему сосуда, т.е. это состояние наиболее вероятно.

Если в качестве примера взять 12 молекул, то результат еще более убедительный, это видно из приведенной ниже таблицы (верхняя строка – соотношение числа молекул, нижняя – число способов такого распределения)

Из этого опыта видно, что наиболее вероятным является такое состояние, в котором равномерно по объему распределены молекулы и их энергии, т.е. состояние термодинамического равновесия. В это состояние в конце концов переходят все изолированные системы и в этом состоянии энтропия максимальна. Больцман установил, что энтропия системы S связана с вероятностью (статистическим весом) состояния системы W соотношением

S = k·ln(W),

где постоянная Больцмана k =1,38·10^-23 Дж/К.

Статистический вес состояния системы W экспоненциально растет с ростом S. Иными словами, менее упорядоченное состояние (больший хаос) имеет больший статистический вес, т. к. оно может быть реализовано большим числом способов. Следовательно, энтропия - мера неупорядоченности (беспорядка) системы. Наиболее вероятным состоянием, соответствующим максимуму энтропии, будет равномерное распределение молекул, при этом реализуется и максимальный «беспорядок»

Современная формулировка второго закона термодинамики: все самопроизвольные процессы в природе идут так, что системы переходят из менее вероятного состояния в более вероятное.

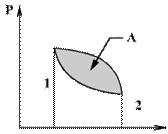
5. Круговым процессом (или циклом) называется такой процесс при котором система после ряда изменении возвращается в исходное состояние.

V

На графике цикл изображается замкнутой кривой. Работа расширения газа из 1 в 2 положительная и равна площади под верхней кривой. Работа сжатия из 2 в 1 отрицательная и равна площади под нижней кривой, поэтому работа, совершаемая при круговом процессе, численно равна разности площадей, то есть равна площади охватываемой замкнутой кривой.

После совершения цикла система возвращается в прежнее состояние. Поэтому всякая функция состояния системы, в частности ее внутренняя энергия, имеет в начале и в конце цикла одинаковое значение.

Тепловые машины построены на принципе круговых процессов.

Тепловая машина состоит из нагревателя, рабочего тела (вещества) и охладителя. В качестве рабочего тела используется пар или газ. Получая теплоту Q1 от нагревателя, газ расширяется и совершает работу, т.е. Q1 = U2 – U1 + A12. Отдавая тепло холодильнику, газ сжимается и - Q2 = U1 – U2 + A21. Складывая эти два выражения, получим Q1- Q2 = A12+ A21 = А (полная работа).

Коэффициент полезного действия тепловой машины

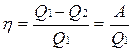
Для получения максимального КПД надо проводить все процессы по возможности обратимо, так как при необратимых процессах теряется тепло бесполезно.

Анализируя работу тепловых двигателей, французский инженер С. Карно в 1824г. пришел к выводу, что наивыгоднейшим круговым процессом является обратимый круговой процесс, состоящий из двух изотермических и двух адиабатических процессов, т.к. он характеризуется наибольшим коэффициентом полезного действия. Такой цикл получил название цикла Карно. В прямом цикле Карно рабочее тело изотермически, а затем адиабатически расширяется, после чего снова изотермически (при более низкой температуре) и потом адиабатически сжимается. Т.е. цикл Карно ограничен двумя изотермами и двумя адиабатами.