Кинематика и динамика материальной точки. 3 страница

где V – скорость волны в среде, y - расстояние от источника колебаний до колеблющейся частицы.

Это уравнение можно записать в виде

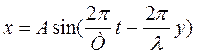
Обозначим 2π/λ = k, эта величина называется волновым числом. Тогда получим следующее уравнение

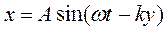
которое называется уравнением плоской одномерной волны и определяет смещение любой точки среды, находящейся на расстоянии y от излучателя в данный момент.

Величина (ωt – ky) называется фазой волны. Зафиксируем какое-либо значение фазы, положив ее постоянной для данной точки 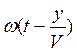= cons. Это выражение дает связь между временем t и координатой х, в которой зафиксированное значение фазы осуществляется в данный момент. Определив 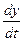, мы найдем скорость, с которой перемещается данное значение фазы. Дифференцируя это соотношение, получим 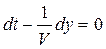, откуда .

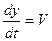Таким образом, скорость распространения волны V в уравнении волны есть скорость перемещения фазы, поэтому ее называют фазовой скоростью.

Геометрическое место точек, колеблющихся в одной фазе, называется волновой поверхностью. Волновая поверхность, отделяющая часть пространства, в которой колебания происходят, от той части, где еще нет колебаний, называется фронтом волны. Именно фронт волны перемещается со скоростью равной фазовой скорости волны.

Если источник колебаний точечный, то от него распространяется волна во все стороны и фронт волны имеет вид сферы. Вблизи источника уравнение волны имеет вид

,

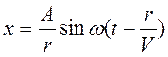где r – расстояние от источника колебаний. Амплитуда сферической волны уменьшается при удалении фронта волны от источника колебаний.

Область пространства, участвующая в волновом процессе, обладает дополнительным запасом энергии. Эта энергия доставляется от источника колебаний в различные точки среды самой волны, следовательно, волна переносит энергию. Численное значение вектора плотности потока энергии определяется следующим образом:

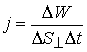
где ΔW - энергия, переносимая за время Δt через площадку ΔS, перпендикулярную к направлению переноса энергии. Другими словами, этот вектор численно равен мощности передаваемой через единичную нормальную к направлению распространения энергии площадку. Направление вектора 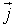совпадает с направлением распространения энергии волны. Эта величина носит название вектора плотности потока энергии. Вектор плотности потока энергии был впервые определен русским ученым Н.А. Умовым и называется вектором Умова.

Среднее по времени значение плотности потока энергии равно:

,

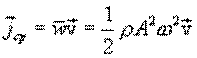где ρ – плотность среды.

2. Когда две одинаковые волны с равными амплитудами и периодами распространяются навстречу друг другу, то при их наложении возникают стоячие волны. Стоячие волны могут быть получены при отражении от препятствий. Допустим, излучатель посылает волну к препятствию (падающая волна). Отраженная от него волна наложится на падающую волну. Уравнение стоячей волны можно получить сложением уравнения падающей волны

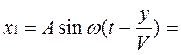
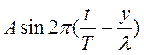
и уравнения отраженной волны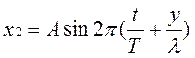

Отраженная волна движется в направлении, противоположном падающей волне, поэтому расстояние х берем со знаком минус. Смещение точки, которая участвует одновременно в двух колебаниях, равно алгебраической сумме х=х1+х2. После несложных преобразований, получаем

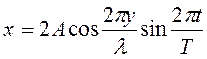
Это уравнение стоячей волны определяет смещение любой точки волны.

Величина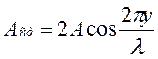

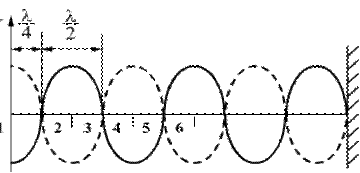не зависит от времени и определяет амплитуду любой точки с координатой y. Каждая точка совершает гармоническое колебание с периодом Т. Амплитуда А_ст для каждой точки вполне определена. Но при переходе от одной точки волны к другой она изменяется в зависимости от расстояния y. Если придавать y значения, равные 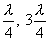и т.д., то получим 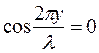. Следовательно, указанные точки волны остаются в покое, т.к. амплитуды их колебаний равны нулю. Эти точки называются узлами стоячей волны. Точки, в которых колебания происходят с максимальной амплитудой, называются пучностями.

х

Расстояние между соседними узлами (или пучностями) называются длиной стоячей волны и равно λ/2 = λст, где λ - длина бегущей волны.

В стоячей волне все точки среды, в которой они распространяются, расположенные между двумя соседними узлами, колеблются в одной фазе. Точки среды, лежащие по разные стороны от узла, колеблются в противофазе -фазы их отличаются на π. т.е. при переходе через узел фаза колебаний скачкообразно меняется на π. В отличие от бегущих волн в стоячей волне отсутствует перенос энергии вследствие того, что образующие эту волну прямая и обратная волны переносят энергию в равных количествах и в прямом и в противоположном направлениях. В том случае, когда волна отражается от среды более плотной, чем та среда, где распространяется волна, в месте отражения возникает узел, фаза изменяется на противоположную. При этом говорят, что происходит потеря половины волны. Когда волна отражается от среды менее плотной в месте отражения, появляется пучность, и потери половины волны нет.

3. 3. Механические колебания в упругих средах вызывают распространение упругих волн, называемых акустическими колебаниями. Физическое понятие об акустических колебаниях охватывает слышимые и неслышимые колебания упругих сред. Распространяясь в пространстве, звуковые колебания создают акустическое поле.

Звуковыми (или акустическими) волнами называются распространяющиеся в среде упругие волны, обладающие частотами в пределах 16—20000 Гц. Волны указанных частот, воздействуя на слуховой аппарат человека, вызывают ощущение звука. Волны с  < 16 Гц (инфразвуковые) и  > 20 кГц (ультразвуковые) органами слуха человека не воспринимаются. Наиболее чувствительно человеческое ухо к диапазону звуковых волн от 1000 до 3000 Гц.

Звуковые волны в газах и жидкостях могут быть только продольными, так как эти среды обладают упругостью лишь по отношению к деформациям сжатия (растяжения). В твердых телах звуковые волны могут быть как продольными, так и поперечными, так как твердые тела обладают упругостью по отношению к деформациям сжатия (растяжения) и сдвига.

Интенсивностью звука (или силой звука) называется величина, определяемая средней по времени энергией, переносимой звуковой волной в единицу времени сквозь единичную площадку, перпендикулярную направлению распространения волны:

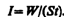
Единица интенсивности звука в СИ — ватт на метр в квадрате (Вт/м²).

Чувствительность человеческого уха различна для разных частот. Для того чтобы вызвать звуковое ощущение, волна должна обладать некоторой минимальной интенсив­ностью, но если эта интенсивность превышает определенный предел, то звук не слышен и вызывает только болевое ощущение. Таким образом, для каждой частоты колебаний существуют наименьшая (порог слышимости) и наибольшая (порог болевого ощущения) интенсивности звука, которые способны вызвать звуковое восприятие.

Звуковое давление человек субъективно воспринимает как громкость звука.
Увеличению громкости в 2 раза соответствует увеличение звукового давления в 10 раз (мощности в 100 раз), увеличению громкости в 3 раза соответствует увеличение звукового давления в 100 раз (мощности в 10 000 раз) и т.д. Таким образом, в психоакустическом восприятии звука наблюдается логарифмическая зависимость, что делает удобным использование относительных единиц – децибел. Один децибел - это минимальное изменение уровня звукового сигнала, которое способен воспринять слух человека.
Разница между минимальным и максимальным уровнями различимых звуковых ощущений называется динамическим диапазоном слуха, который составляет приблизительно 120дБ. Болевой порог соответствует звуковому давлению 200Па (на частоте 1кГц).

Звук характеризуется помимо громкости еще высотой и тембром. Высота звука — качество звука, определяемое человеком субъективно на слух и зависящее от частоты звука. С ростом частоты высота звука увеличивается, т. е. звук становится «выше». Характер акустического спектра и распределения энергии между определен­ными частотами определяет своеобразие звукового ощущения, называемое тембром звука. Так, различные певцы, берущие одну и ту же ноту, имеют различный акустичес­кий спектр, т. е. их голоса имеют различный тембр.

Скорость распространения звуковых волн в газах вычисляется по формуле

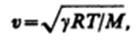
где R — молярная газовая постоянная, М — молярная масса, =С_р/С_V — отношение молярных теплоемкостей газа при постоянных давлении и объеме, Т —термодинамическая температура. Из формулы вытекает, что скорость звука в газе не зависит от давления р газа, но возрастает с повышением температуры. Чем больше молярная масса газа, тем меньше в нем скорость звука. Например, при T=273 К скорость звука в воздухе (M=2910^–3 кг/моль) v=331 м/с, в водороде (M=210^–3 кг/моль) v=1260 м/с.

Инфразвук (ИЗ) — колебания частотой ниже 20 Гц. Подавляющее число современных людей не слышат акустические колебания частотой ниже 40 Гц. Максимальные уровни низкочастотных акустических колебаний от промышленных и транспортных источников достигают 100–110 дБ.

Допустимыми уровнями звукового давления являются 105 дБ в октавных полосах 2, 4, 8, 16 Гц и 102 дБ в октавной полосе 31.5 Гц. Инфразвук может вселить в человека такие чувства как тоска, панический страх, ощущение холода, беспокойство, дрожь в позвоночнике. Люди, подвергшиеся воздействию инфразвука, испытывают примерно те же ощущения, что и при посещении мест, где происходили встречи с призраками. Попадая в резонанс с биоритмами человека, инфразвук особо высокой интенсивности может вызвать мгновенную смерть.

При совпадении частот внутренних органов и инфразвука, соответствующие органы начинают вибрировать, что может сопровождаться сильнейшими болевыми ощущениями. При воздействии на человека инфразвука с частотами, близкими к 6 Гц, могут отличаться друг от друга картины, создаваемые левым и правым глазом, начнет «ломаться» горизонт, возникнут проблемы с ориентацией в пространстве, придут необъяснимая тревога, страх. Подобные ощущения вызывают и пульсации света на частотах 4–8 Гц. Инфразвук может действовать не только на зрение, но и на психику, а также шевелить волоски на коже, создавая ощущение холода

УЛЬТРАЗВУК (УЗ) — упругие волны с частотой колебаний от 20 кГц до 1 ГГц, не слышимые человеческим ухом. Ультразвуковые волны по своей природе не отличаются от упругих волн слышимого диапазона. Распространение УЗ подчиняется основным законам, общим для акустических волн любого диапазона частот. Вместе с тем высокая частота ультразвуковых колебаний и малая длина волн обусловливают ряд специфических свойств, присущих только УЗ. Вследствие большой частоты (малой длины волны) ультразвук обладает особыми свойствами. Так, подобно свету, ультразвуковые волны могут образовывать строго направленные пучки. Отражение и преломление этих пучков на границе двух сред подчиняется законам геометрической оптики. Он сильно поглощается газами и слабо - жидкостями., отражается от границ раздела твердых и жидких сред с газами.

Ультразвуковые колебания возникают при работе моторов автомобилей, станков и ракетных двигателей. В практике для получения ультразвука обычно применяют электромеханические генераторы ультразвука, действие которых основано на способности некоторых материалов изменять свои размеры под действием магнитного (магнитострикционные генераторы) или электрического поля (пьезоэлектрические генераторы), при этом генераторы издают звуки высокой частоты.
В жидкости под воздействием ультразвука образуются пустоты в виде мельчайших пузырьков с кратковременным возрастанием давления внутри них. Кроме того, ультразвуковые волны ускоряют протекание процессов диффузии (взаимопроникновения двух сред друг в друга). Ультразвуковые волны существенно влияют на растворимость вещества и в целом на ход химических реакций. Эти свойства ультразвука и особенности его взаимодействия со средой обусловливают его широкое техническое и медицинское использование. Ультразвук применяют в медицине и биологии для диагностики, для выявления и лечения опухолей и некоторых дефектов в тканях организма.

У. широко применяется в технике. По данным измерений с и a во многих техн. задачах осуществляется контроль за протеканием того или иного процесса (контроль концентрации смеси газов, состава разл. жидкостей и т. п.). Используя отражение У. на границе разл. сред, с помощью УЗ-приборов измеряют размеры изделий (напр., УЗ-тол-щиномеры), определяют уровни жидкостей в ёмкостях, недоступных для прямого измерения. У. сравнительно малой интенсивности (~0,1 Вт/см²) применяется в дефектоскопии для неразрушающего контроля изделий из твёрдых материалов (рельсов, крупных отливок, качественного проката и т. д.). При помощи У. осуществляется звукови-дение: преобразуя УЗ-колебания в электрические, а последние в световые, оказывается возможным при помощи У. видеть те или иные предметы в непрозрачной для света среде. Для получения увеличенных изображений предмета с помощью У. высокой частоты создан акустич. микроскоп, аналогичный обычному микроскопу, преимущества к-рого перед оптическим - высокая контрастность и возможность получать изображения оптически непрозрачных объектов.

Лекция 7

Тема:Основы молекулярно-кинетической теории

Вопросы:1) Статистический метод в физике

2) Основное уравнение молекулярно-кинетической теории

3) Внутренняя энергия газа

4) Явления переноса

1. Молекулярная физика и термодинамика - разделы физики, в которых изучается макроскопические процессы в телах, связанные с огромным числом содержащихся в них атомов и молекул. Для исследования этих процессов применяют два качественно различных и взаимно дополняющих друг друга метода: статический (молекулярно-кинетический) и термодинамический. В основе молекулярной физики лежит статический метод

Молекулярная физика раздел физики, в котором изучаются строение и свойства вещества исходя из молекулярно-кинетических представлений, основывающихся на том, что все тела состоят из молекул, находящихся в непрерывном хаотическом движении.

Движение молекул в разных телах происходит по-разному. Молекулы газов беспорядочно движутся с большими скоростями (сотни м/с) по всему объему газа. Сталкиваясь, они отскакивают друг от друга, изменяя величину и направление скоростей. Молекулы жидкости колеблются около равновесных положений (т.к. расположены почти вплотную друг к другу) и сравнительно редко перескакивают из одного равновесного положения в другое случайным образом. Движение молекул в жидкостях является менее свободным, чем в газах, но более свободным, чем в твердых телах. В твердых телах частицы сильно связаны, поэтому только колеблются около положения равновесия. Между ними действуют силы притяжения и отталкивания (см. рис.).

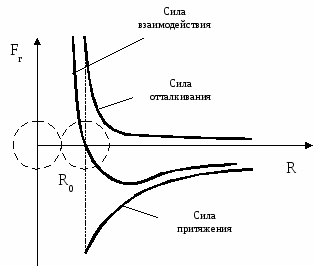
При образовании кристалла из раствора или расплава молекулы (атомы, ионы) занимают положения, в которых эти силы уравновешивают друг друга (расстояние R0) между частицами.

С ростом температуры скорость частиц увеличивается, поэтому хаотическое движение частиц принято называть тепловым.

Модель идеального газа – твёрдые шарики одного диаметра, взаимодействующие между собой только при столкновении. В момент столкновения молекула резко изменяет величину и направление скорости своего движения. Расстояние, проходимое молекулой в среднем без столкновений, называется средней длиной свободного пробега.

Скорости молекул газа имеют различные значения и направления, причем из-за огромного числа соударений, которые ежесекундно испытывает молекула, скорость ее постоянно изменяется. В этом случае не имеет смысла применять динамический метод, основанный на законах Ньютона - нельзя определить число молекул, которые обладают точно заданной скоростью v в данный момент времени. Максвелл разработал статистический метод, по которому можно подсчитать долю молекул, скорости которых имеют значение, лежащие между некоторыми скоростями v₁ и v₂ . На основании теории вероятности Максвелл установил закономерность (функцию f(v)), по которой можно определить долю от общего числа молекул газа N, скорости которых при данной температуре заключены в интервале скоростей от v до v+dv:

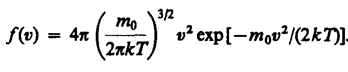
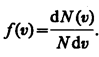
, где

Видно, что конкретный вид функции зависит от рода газа (от массы молекулы m0) и от параметра состояния (температуры Т). В формуле k – постоянная Больцмана, равная 1, 38·10 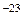Дж/К.

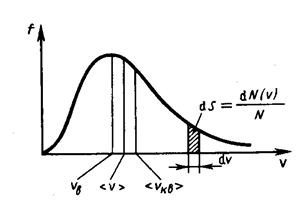
Распределение Максвелла достигает максимума при наиболее вероятной скорости 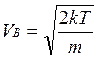, т.е. такой скорости, к которой близки скорости большинства молекул. Здесь m – масса одной молекулы газа.

Площадь заштрихованной полоски с основанием dV покажет, какая часть от общего числа молекул имеет скорости, лежащие в данном интервале. Конкретный вид функции распределения Максвелла зависит от рода газа (массы молекулы) и температуры. Давление и объем газа на распределение молекул по скоростям не влияет. С повышением температуры наиболее вероятная скорость возрастает, поэтому максимум распределения молекул по скоростям сдвигается в сторону больших скоростей, а его абсолютная величина уменьшается, т.к. общее число молекул (площадь под кривой) не изменяется (см. рисунок ниже).

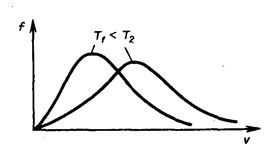
Следовательно, при нагревании газа доля молекул, обладающих малыми скоростями уменьшается, а доля молекул с большими скоростями увеличивается.

Таким образом, в газе, находящемся в состоянии равновесия, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоро­стям, которое подчиняется вполне определенному статистическому закону. Из него вытекает также, что как бы ни изменялись скорости молекул при столкновениях, средняя квадратичная скорость молекул массой т₀ в газе, находящемся в состоянии равновесия при Т= const. остается постоянной и равной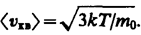

Распределение Максвелла позволяет найти среднюю арифметическую скорость молекул:

.

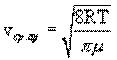При комнатной температуре T=300K средняя арифметическая скорость молекул кислорода будет равна ≈500 м/с.

Первое экспериментальное определение скоростей молекул было осуществлено Штерном в 1920 г: подтвердилась правильность оценки средней скорости молекул, вытекающей из распределения Максвелла.

Экспериментальная установка представляет собой два находящихся в вакууме жестко связанных между собой коаксиальных цилиндра (см. рис.), по оси которых натянута платиновая нить, покрытая серебром. Малый цилиндр радиуса rимеет вертикальную щель.

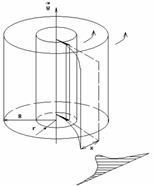
Если по нити пропустить электрический ток, она будет нагреваться, серебро будет испарятся, его атомы будут пролетать через щель и осаждаться на большом цилиндре радиуса R, образуя изображение узкой щели в виде узкой полоски почернения серебра. Картина изменится, если установку привести во вращение с угловой скоростью w, при этом полоска смещается в сторону противоположную вращению на величину 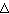=AA'. Смещение возникало, потому что за время t пролета атомом серебра расстояния R-r цилиндр успевал повернуться на угол 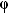= 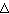/R = 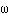t. Откуда определялось время t = 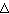/ 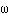R, знание которого позволяло найти скорость атома серебра через измеримые параметры опыта:

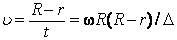
Как следовало ожидать, полоска серебра в положении А' оказывалась размытой из-за того, что атомы серебра имеют разные скорости: более быстрым атомам соответствуют меньшие, а более медленным – большие смещения 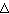. Исследуя зависимость плотности серебра в размытой части от расстояния до точки A, нетрудно оценить распределение атомов серебра по скоростям. Полученное распределение хорошо согласовывалось со значениями, вычисленными по формуле Максвелла.

Применяя статистический метод, Больцман получил распределение молекул газа в гравитационном поле:

,

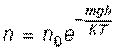где n – число молекул газа в единице объема (концентрация) на высоте h, n0 – концентрация молекул газа на нулевом уровне (уровне земли)

Больцман показал, что полученное распределение применимо к идеальному газу, находящемуся в любом силовом поле.

2. Результаты экспериментальных и теоретических исследований позволили уже в девятнадцатом веке сформулировать основные положения молекулярно-кинетической теории для газов:

· газ состоит из молекул (мельчайших частиц, размеры которых порядка 10^{-10 м});

· молекулы газа находятся в непрерывном хаотическом движении;

· молекулы сталкиваются друг с другом. Столкновения бывают упругими (низкие температуры) и неупругими (высокие температуры);

· в промежутке между соударениями молекулы движутся прямолинейно;

· молекулы на малых расстояниях отталкиваются, а на больших притягиваются друг к другу.

Для объяснения свойств вещества в газообразном состоянии используется модель идеального газа. В модели идеального газа предполагается следующее: молекулы обладают пренебрежимо малым объемом по сравнению с объемом сосуда, между молекулами не действуют силы притяжения, при соударениях молекул друг с другом и со стенками сосуда действуют силы отталкивания.

При упругом столкновении молекулы со стенкой сосуда проекция vх вектора скорости на ось ОХ, перпендикулярную стенке, изменяет свой знак на противоположный, но остается постоянной по модулю (см.рис).

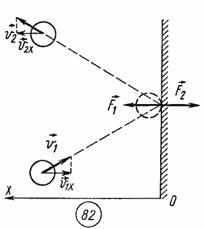
Поэтому в результате столкновения молекулы со стенкой проекция ее импульса на ось ОХ изменяется от mv1х = - mvх до mv2х = mvх. Изменение импульса молекулы показывает, что на нее при столкновении действует сила 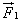, направленная от стенки. Изменение импульса молекулы равно импульсу силы:

.

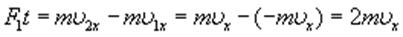Во время столкновения молекула действует на стенку с силой 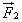, равной по третьему закону Ньютона силе 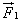по модулю и направленной противоположно.

Молекул газа очень много, и удары их о стенку следуют один за другим с очень большой частотой. Среднее значение геометрической суммы сил, действующих со стороны отдельных молекул при их столкновениях со стенкой сосуда, и является силой давления газа. Давление газа равно отношению модуля силы давления 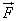к площади стенки S:

.

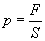На основе использования основных положений молекулярно-кинетической теории было получено уравнение, которое позволяет вычислить давление газа, если известны масса m молекулы газа, среднее значение квадрата скорости молекул 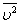и концентрация n молекул:

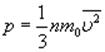
Среднее значение кинетической энергии молекул идеального газа

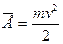, получим .

Давление идеального газа равно двум третям средней кинетической энергии движения молекул, содержащихся в единице объема.

Опыт показывает, что давление и температура газа связаны, поэтому английским физиком Кельвином была введена абсолютная температура Т как мера средней энергии движения молекул вещества:

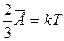
Здесь k - постоянная Больцмана, k = 1,38*10^-23 Дж/К. За ноль абсолютной температуры принята такая температура по шкале Кельвина, при которой прекращается всякое движение молекул вещества, т.е. .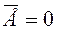

Связь температур, измеряемых в шкале Кельвина Т и шкале Цельсия t, имеет вид
Т = t + 273.

В результате было получено выражение, связывающее давление и температуру идеального газа

p= nkT,

которое называется основным уравнением молекулярно-кинетической теории газа.

В результате преобразования этого выражения было получено уравнение состояния идеального газа (уравнение Менделеева-Клапейрона)

,

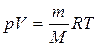где универсальная газовая постоянная R = 8,31 Дж/(моль·К), М - молярная масса газа, m – масса газа, V – объем газа.

Основной закон молекулярно-кинетической теории позволил рассчитать среднюю длину свободного пробега молекул газа между соударениями

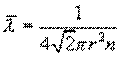
r– размер молекулы, n – число молекул в единице объема газа.

В воздухе при нормальных условиях (давление 1 атм, температура 273 К) средняя длина свободного пробега молекулы составляет порядка 0,6 ·10 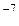м, при этом в единице объема газа каждую секунду совершается порядка 8,6·10 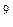столкновений молекул.

3. Молекулы можно рассматривать как системы материальных точек (атомов) совершающих как поступательное, так и вращательное движения. При исследовании движения тела необходимо знать его положение относительно выбранной системы координат. Для этого вводится понятие о степенях свободы тела. Число независимых координат, которые полностью определяют положение тела в пространстве, называется числом степеней свободы тела.

При движении точки по прямой линии для оценки ее положения необходимо знать одну координату, т.е. точка имеет одну степень свободы. Если точка движения по плоскости, ее положение характеризуется двумя координатами; при этом точка обладает двумя степенями свободы. Положение точки в пространстве определяется 3 координатами. Число степеней свободы обычно обозначают буквой i. Молекулы, которые состоят из обычного атома, считаются материальными точками и имеют три степени свободы (аргон, гелий).