Построение сечений тора

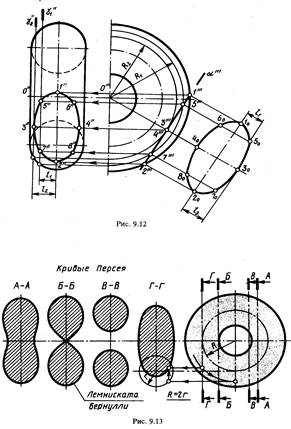
Рис. 12

В примере на рис. 12 показано применение вспомогательных плоскостей γ₁(γ₁") и γ₂(γ₂") , перпендикулярных оси тора, для построения линии пересечения и натурального вида фигуры сечения поверхности тора плоскостью α (α'"). Тор на рис.12 имеет два изображения - фронтальную проекцию и половину профильной проекции.

Полуокружность радиуса R₂ (профильная проекция линии пересечения тора вспомогательной

плоскостью γ₂) касается проекции плоскости α(следа α'"). Тем самым определяются профильная проекция 3'" и по ней фронтальная проекция 3'" одной из точек проекции искомой линии пересечения. Полуокружность радиуса R₁ - профильная проекция линии пересечения тора вспомогательной плоскостью γ₁ . Она пересекает профильную проекцию плоскости α (след α'") в двух точках 5'" и 7'" - профильных проекциях точек линии пересечения. Проводя аналогичные пост­роения, можно получить необходимое количество проекций точек для искомой линии пересечения. Используем найденные точки для построения натурального вида фигуры сечения. Фигура сечения тора плоскостью, параллельной его оси, имеет оси и центр симметрии. При ее построении использованы расстояния l₁ и l₂ на фронтальной проекции для нанесения точек 5₀, 7₀ и 3₀.

Точки 6₀ , 8₀ и 4₀ построены как симметричные. Построенная кривая пересечения поверхности тора плоскостью выражается ал­гебраическим уравнением 4-го порядка.

Кривые пересечения тора с плоскостью, параллельной оси, приведены на рис.12 внизу. Они имеют общее название - кривые Персея (Персей — геометр Древней Греции). Это кривые четвертого порядка. Вид кривых зависит от величины расстояния от секущей плоскости до оси тора.