Последовательность построения 2-х многогранников
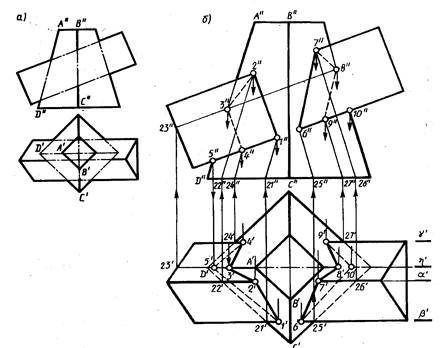
Рис. 6
Рис. 6, а. Прежде чем приступить к построениям, анализируют взаимное положение многогранников и их расположение относительно плоскостей проекций. В данном случае очевидно, что многогранники могут пересекаться только по боковым граням. Ребра призмы и боковые ребра пирамиды параллельны плоскости π2, основания пирамиды параллельны плоскости π1. Нижняя грань призмы и ее основания перпендикулярны плоскости π1.
Указанные особенности расположения призмы и пирамиды определяют и наиболее рациональный способ построения линии пересечения их поверхностей по точкам пересечения ребер призмы с гранями пирамиды и боковых ребер пирамиды с гранями призмы.
Построения показаны на рис. 6, б. Рассмотрим их для левой части чертежа (от оси пирамиды). Проекции 1", 1', 2", 2', 3", 3' ,4", 4' точек пересечения ребер призмы с гранями пирамиды найдены путем проведения через них фронтальных плоскостей β (β'), α (α'), γ (γ'). Они пересекают левые боковые грани пирамиды по фронталям - прямым линиям, параллельным левому ребру пирамиды. Положение их фронтальных проекций определено по горизонтальным проекциям 21', 22', и 24' точек пересечения горизонтальных проекций β', α' и γ' плоскостей β, α, γ с горизонтальной проекцией основания пирамиды. В пересечении фронтальных проекций этих линий с фронтальными проекциями ребер призмы найдены фронтальные проекции 1", 2" и 4" точек пересечения ребер призмы с левыми гранями пирамиды. По ним построены горизонтальные проекции 1', 2', 4'.
Проекции 3", 3' точки пересечения ребер AD пирамиды с верхней задней гранью призмы найдены с помощью вспомогательной фронтальной плоскости η(η'), которая проведена через это ребро. Плоскость η пересекает грань призмы по прямой, параллельной ребрам призмы и проходящей через точку 23 на основании призмы. В пересечении фронтальных проекций этой прямой и ребра А" D" найдена фронтальная проекция 3" точки пересечения указанного ребра с задней верхней гранью призмы и на линии связи - горизонтальная проекция 3'. С нижней гранью призмы, перпендикулярной плоскости π2 , ребро AD пересекается в точке с фронтальной проекцией 5 ". В проекционной связи на проекции А' D' построена ее горизонтальная проекция 5'.
Таким образом, проекции точек пересечения всех ребер призмы с левыми гранями пирамиды - 1", 1', 2", 2', 4", 4' и ребра AD пирамиды с двумя гранями призмы - 3", 3' и 5", 5' построены. Соединяем проекции точек, принадлежащих одной грани, и получаем проекции 1" 2" 3" 4" 5" 1" , 1' 2' 3' 4' 5' 1' ломаной линии пересечения.
Построение в правой части чертежа проекции 6" 7" 8" 9" 10" 6", 6' 7' 8' 9' 10' 6' линии пересечения аналогично. Порядок построения иллюстрируется стрелками.
После построения проекций линий пересечения многогранников обводят проекции оставшихся частей ребер многогранников.
Заметим, что переднее и заднее ребра пирамиды не пересекают поверхность призмы.
Дата добавления: 2015-09-07; просмотров: 1029;
