Построение сечения конуса и его развертки

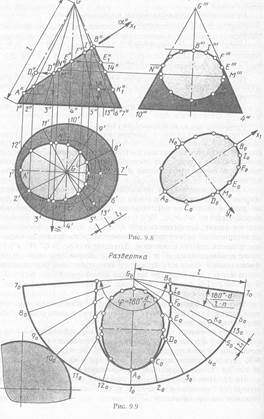
Рис. 10

Развертка боковой поверхности прямого кругового конусапред­ставляет собой круговой сектор с углом φ = d/l × 180 ° при вершине, где d - диаметр основания, l - длина образующей конуса. Пост­роение сектора (рис. 10 внизу) выполняют с разбивкой его на равные части соответственно разметке образующих на чертеже (см. рис. 10 конуса).

Используя положение образующих на чертеже и на развертке находят положение точек на развертке при помощи натуральных величин отрезков от вершины до соответствующих точек линии пересечения на чертеже. При этом расстояния G₀A₀ и G₀B₀ соответ­ствуют фронтальным проекциям G"А " С"В". Отрезки образующих от вершины до других точек проецируются на фронтальную плос­кость проекций с искажениями. Поэтому их натуральную величину находят вращением вокруг оси конуса до положения, параллельного фронтальной плоскости проекций. Например, положение точки D₀ на развертке найдено при помощи отрезка G "D₁" - натуральной величины образующей от вершины G до точки D точки E₀, - при помощи отрезка G"Е₁" (или G'"E'").

Полная развертка поверхности усеченного конуса состоит из трех частей: 1) развертки боковой поверхности, ограниченной дугой окружности радиуса l, кривой B₀I₀F₀E₀D₀C₀A₀ и симметричной ей; круга основания; 3) натурального вида фигуры сечения.

На рис. 10 (вверху) показано построение фронтальной и горизонтальной проекций точки К по изображению К₀ этой точки на развертке (рис.10). Для построения проведена образующая G₀13₀ через точку К₀ на развертке. С помощью отрезка l₁ построена горизонтальная проекция 13'. Через нее проведены горизонтальная G' 13' и фронталь­ная G"13 " проекции образующей G - 13. Отрезок G₀K₀ = G"K₁" на проекции образующей G "7 ". Обратным вращением построена фронтальная проекция К" точки К на фронтальной проекции образующей G"13".Горизонтальная проекция К' построена с помощью линии связи.