Пересечение пирамиды линией и призмой

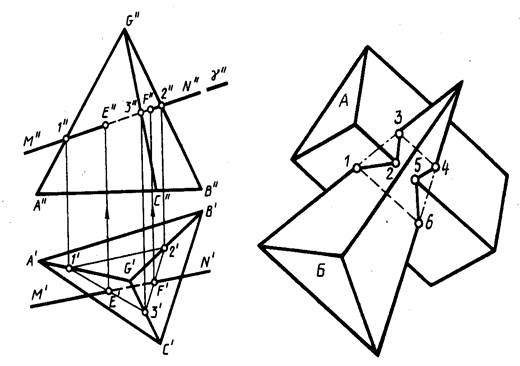
Рис. 5

Построение точек пересечения прямой с поверхностью многогранника сводится к построению линии пересечения многогранника проецирующей плоскостью, в которую заключают данную прямую. На рис. 5(слева) приведено построение проекций Е", Е' и F", F' точек пересечения прямой с проекциями M"N", M'N' с боковыми гра­нями пирамиды. Пирамида задана проекциями G", G' вершины и А"В"С",А'В'С основания. Прямая MN заключена во вспомо­гательную фронтальную проецирующую плоскость γ(γ"). Горизон­тальные проекции Е' и F' искомых точек построены в пересечении проекции M'N' с горизонтальными проекциями 1', 3' и 2', 3' отрезков, по которым плоскость γ пересекает боковые грани пирамиды. Фрон­тальные проекции Е" и F" определены по линиям связи.

Изображение пересекающихся междусобой в пространстве призмы А и пирамиды Б представлено на рис. 5(справа). Линия их пересечения проходит через точки 1, 3, 4, 6 пересечения ребер пирамиды с гранями призмы и точки 2, 5 пересечения ребра призмы

с гранями пирамиды. В общем случае в пересечении многогранников получается пространственная замкнутая ломаная линия, котораяв некоторых частных случаях может оказаться плоской. При построении линии пересечения многогранников применя­ют два способа и их комбинации.

1. Строят точки пересечения ребер одного многогранника с гранями другого и Ребер второго с гранями первого. Через постро­енные точки в определенной последовательности проводят ломаную линию пересечения данных многогранников. При этом отрезки прямых проводят лишь через те построенные точки, которые лежат в одной и той же грани.

2. Строят отрезки прямых, по которым грани одной поверхности пересекают грани другой. Эти отрезки являются звеньями ломаной линии пересечения многогранных поверхностей между собой.

Таким образом, построение линии пересечения двух много­гранников сводится или к построению линии пересечения двух плоскостей между собой, или к построению точки пересечения прямой с плоскостью