Призма и пирамида
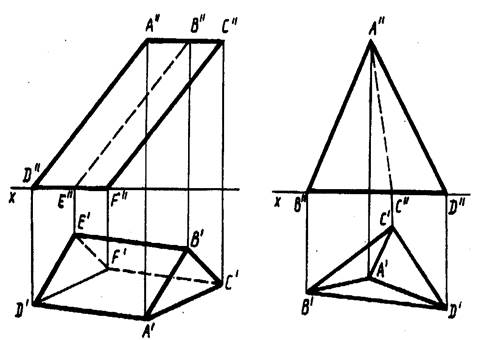
Рис. 1
Призматическая поверхность неограниченной длины на чертеже может быть изображена проекциями фигуры, полученной при пересечении боковых граней призмы плоскостью, и проекциями ребер призмы. Пересекая призматическую поверхность двумя параллельными между собой плоскостями, получают основания призмы. На чертеже основания призмы удобно располагать параллельно плоскости проекций. Чертеж призмы с проекциями оснований А"В"С", А'В'С и D"E"F", D'E'F' , параллельных плоскости π1 , приведен на
рис.1 (слева). Одноименные проекции ребер призмы параллельны между собой.
Для изображения поверхности пирамиды на чертеже используют фигуру сечения боковых граней пирамиды плоскостью и точку из пересечения - вершину. На чертеже пирамиду задают проекциями ее основания, ребер и вершины, усеченную пирамиду - проекциями обоих оснований и ребер.
Изображая пирамиду, удобно ее основание располагать параллельно плоскости проекций.
На рис. 1 (справа) приведен чертеж неправильной треугольной пирамиды с проекциями А", А' вершины и основанием, проекции которого D"B"C" и D'B'C, лежащим в плоскости проекций π1.
Дата добавления: 2015-09-07; просмотров: 1061;
