Бипризма Френеля

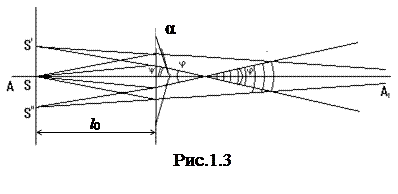При наблюдении интерференции света с помощью би­приз­мы Фре­не­ля, как и в опыте Юнга, ис­кус­ст­вен­но соз­да­ют­ся ко­ге­рент­ные пучки пу­тем разделения и последующего сведения световых лучей, исходящих из одного и того же источника. Би­приз­ма Фре­не­ля пред­став­ля­ет со­бой сим­мет­рич­ную стек­лян­ную приз­му с очень ма­лы­ми пре­лом­ляю­щи­ми уг­ла­ми α (рис.1.3).

Ис­то­ч­ни­ком све­та слу­жит уз­кая щель S, рас­по­ло­жен­ная па­рал­лель­но ре­б­ру ту­по­го уг­ла би­приз­мы. При этом лу­чи, про­шед­шие от ще­ли ­че­рез верх­нюю и ни­ж­нюю по­ло­ви­ны би­приз­мы, от­кло­ня­ют­ся к ли­нии АА₁. В ча­с­ти про­стран­с­т­ва (на ри­с.1.3 оно за­штри­хо­ва­но) бу­дут рас­про­стра­нять­ся све­то­вые во­л­ны, про­шед­шие че­рез верх­ню­ю и ни­ж­нюю по­ло­ви­ны би­приз­мы. Эти во­л­ны мо­ж­но счи­тать ис­хо­дя­щи­ми из двух мни­мых изо­б­ра­же­ний ще­ли S' и S", ко­то­рые мо­ж­но рас­сма­т­ри­вать как два ко­ге­рент­ных ис­то­ч­ни­ка. За­штри­хо­ван­ная об­ласть яв­ля­ет­ся об­ла­стью ин­тер­фе­рен­ции све­та. На эк­ра­не, на­хо­дя­щем­ся в э­той об­ла­с­ти, мо­ж­но ви­деть ин­тер­фе­рен­ци­он­ные свет­лые и тем­ные полосы.

Если преломляющий угол призмы a мал и углы падения лучей на грань не очень большие, то можно показать, что все лучи отклоняются на практически одинаковые углы

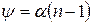, (1.12)

где n – показатель преломления призмы. В результате образуются два мнимых когерентных источника S' и S", лежащие в одной плоскости с источником S. Уг­ло­вая ши­ри­на зо­ны ин­тер­фе­рен­ции (угол j) за­ви­сит толь­ко от свойств би­приз­мы:

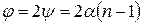. (1.13)

Угол j вслед­ст­вие ма­ло­сти мо­жет быть оп­ре­де­лен с по­мо­щью фор­му­лы:

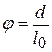, (1.14)

где d – рас­сто­я­ние ме­ж­ду мни­мы­ми ис­то­ч­ни­ка­ми, 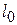– рас­сто­я­ние ме­ж­ду ще­лью и би­приз­мой (рис.1.3).