Метод зон Френеля. Прямолинейное распространение света

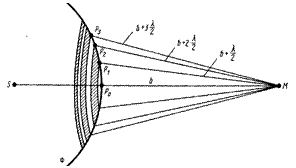Найдем в точке М амплитуду световой волны, распространяющейся в однородной среде из точечной источника S. По принципу Гюйгенса — Френеля, заменим действие источника S действием мнимых источников, расположенных на вспомога­тельной поверхности Ф, являющейся по­верхностью фронта волны, идущей из S (поверхность сферы с центром S). Фре­нель разбил волновую поверхность Ф на кольцевые зоны такого размера, чтобы расстояния от краев зоны до М отлича­лись на 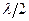. Разбиение фронта волны на зоны можно выполнить, проведя с центром в т. М сферы радиусами 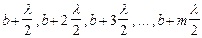, где b-расстояние от вершины волновой поверхности до т. М, а- радиус волновой поверхности. Т. к. колебания от соседних зон проходят до т. М расстояния, отличающиеся на 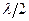, то в т. 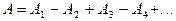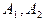М они приходят в противоположной фазе и при наложении эти колебания будут взаимно ослаблять друг друга: , где и т.д. – амплитуды колебаний, возбужденных порознь 1-й, 2-й и т.д. зонами, 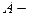амплитуда результирующих колебаний. Величина 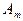амплитуды зависит от площади m-й зоны и угла 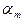между внешней нормалью к поверхности зоны в какой-либо ее точке и прямой, направленной из этой точки в т. М.

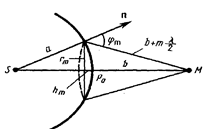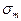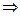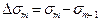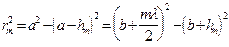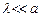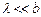Для оценки амплитуд колебаний найдем площади зон Френеля. Внешняя граница т-й зоны выделяет на волновой поверхности сферический сегмент высоты h_m. Пусть площадь сегмента , площадь m-й зоны Френеля , где площадь сферического сегмента, выделяемого внешней границей (m-1)-й зоны. Из рисунка: . Т.к. и , то 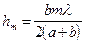. Тогда , а площадь m-й зоны Френеля 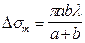(12.1)

Полученное выражение не зависит от т; 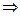при не слишком больших т площади зон Френеля одинаковы. В то же время с увеличением номера зоны возрастает угол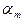 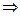уменьшается амплитуда 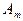(вследствие увеличения расстояния от зоны до т. М)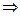

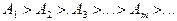
При большом числе зон Френеля 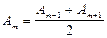, тогда 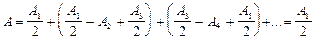. Все выражения, стоящие в скобках, = 0. 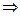результирующее действие в т. М полностью открытого фронта световых волн равно половине действия одной только центральной зоны Френеля, радиус которой сравнительно мал (при 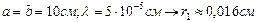). Распростра­нение света от S к М происходит так, будто световой поток распространяется внутри очень узкого канала вдоль SM, т. е. прямолинейно.

Выводы:

1. Построение зон Френеля раз­бивает волновую поверхность сферической волны на равные зоны.

2. Интенсивность излучения в направле­нии т. М уменьшается с ростом т.

3.Общее число зон Френеля, умещаю­щихся на полусфере: 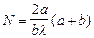(при 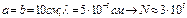) (12.2)

4.Если высота сегмента 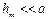(при не слиш­ком больших т), тогда 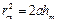. ра­диус внешней границы m-й зоны Френеля для сферической волны: 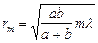(12.3)

Для плоского волнового фронта (для плоской волны) 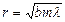(12.3’)

5. Принцип Гюйгенса - Френеля позволяет объяснить прямолинейное распростране­ние света в однородной среде.

Для электромагнитных волн различаются: диф­ракция радиоволн, света и рентгеновских лучей.

По виду волн различаются: дифракция сферических волн и диф­ракция плоских волн.

По роду экранов различаются: дифракция на круглом отверстии и круглом экране, на полубесконечном прямом экране, на длинной узкой ще­ли и длинном узком экране, на прямоугольном отвер­стии и прямоугольном экране, на двух и более узких щелях (дифракционной решетке), а также на многомер­ных структурах.