Метод Юнга.
Для получения интерференционной картины необходимы когерентные световые пучки. До появления лазеров во всех приборах для наблюдения интерференции света когерентные пучки получали методом разделения волны: лучи, исходящие из одного и того же источника, разделяли с помощью экранов со щелями или зеркал, затем полученные таким образом когерентные лучи сводили вместе. Одним из таких способов является метод Юнга. Источником света служит ярко освещенная щель S, от которой свет падает на две равноудаленные щели S1 и S2, параллельные щели S (рис. 1.1). Щели S1 и S2 являются источниками когерентных пучков света.
Результат интерференции колебаний, доходящих до некоторой точки М экрана (рис. 1.2) от источников S' и S", будет зависеть от их разности хода 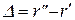 . Если разность хода Δ равна целому числу длин волн l:
. Если разность хода Δ равна целому числу длин волн l:
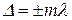 ; (m=0, 1, 2, …), (1.6)
; (m=0, 1, 2, …), (1.6)
то колебания от обоих источников приходят в одной фазе и освещенность в этой точке будет максимальна. Если же 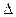 равно полуцелому числу волн:
равно полуцелому числу волн:
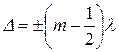 ; (m=1, 2, 3, …), (1.7)
; (m=1, 2, 3, …), (1.7)
то колебания приходят в противофазе и освещенность в этой точке будет минимальна. При других значениях  освещенность будет иметь промежуточное значение.
освещенность будет иметь промежуточное значение.
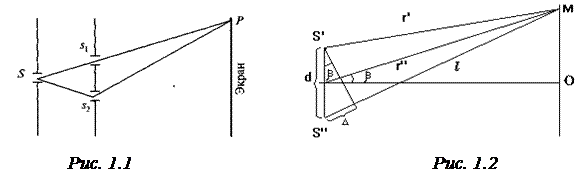 |
Найдём расстояние xm между центральным максимумом (точкой О) и максимумом m-го порядка (рис.1.2). Для получения различимой интерференционной картины расстояние d между источниками должно быть значительно меньше расстояния до экрана 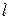 . При этих условиях можно считать угол b достаточно малым, тогда
. При этих условиях можно считать угол b достаточно малым, тогда
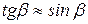 . (1.8)
. (1.8)
Из рис.1.2 можно найти:
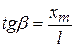 ,
, 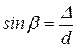 . (1.9)
. (1.9)
Решая уравнения (1.6) и (1.8-1.9) получим:
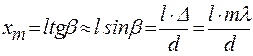 . (1.10)
. (1.10)
Отсюда ширина интерференционной полосы Δx, т.е. расстояние между соседними максимумами или минимумами, равно:
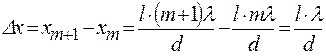 . (1.11)
. (1.11)
В соответствии с (1.11) расстояние между соседними максимумами растёт с уменьшением расстояния d между источниками. При d, сравнимом с 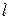 , расстояние между полосами было бы того же порядка, что и λ, то есть отдельные полосы были бы совершенно неразличимы. Для того чтобы интерференционная картина была отчётливой, необходимо выполнение упоминавшегося выше условия: d<<
, расстояние между полосами было бы того же порядка, что и λ, то есть отдельные полосы были бы совершенно неразличимы. Для того чтобы интерференционная картина была отчётливой, необходимо выполнение упоминавшегося выше условия: d<< 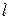 .
.
Дата добавления: 2015-09-07; просмотров: 790;
