Порядок выполнения работы. 2. Измерить x1 – координату середины крайней левой четко видной светлой полосы и xm+1 – координату (m+1) полосы

1. Вклю­чить в сеть лазер. В луч лазера перед бипризмой поставить линзу 2. Она создает источник S₀ и расширяет пучок. Линзу устанавливают так, чтобы фокус ее был перед призмой (точка S₀). Плавно перемещая бипризму в лазерном пучке, добиться четкой интерференционной картины.

2. Измерить x₁ – координату середины крайней левой четко видной светлой полосы и x_m+1 – координату (m+1) полосы, записать в таблицу 1.1.

Таблица 1.1

3. Записать m – количество видных полос.

4. Рассчитать Δx=(x_m+1–x₁)/m – ширину интерференционной полосы.

5. Измерить L – расстояние между линзой и бипризмой и b – расстояние между бипризмой и экраном.

6. Вычислить расстояние между изображениями источника и бипризмой: a=L–F, где F=15 мм - фокусное расстояние линзы.

7. Вычислить значение преломляющего угла бипризмы α и занести в таблицу 1.1. Из формул (1.15) и (1.17) получим:

.

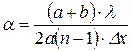8. Повторить измерения по пунктам 2–7 при других положениях линзы или бипризмы. Опыт повторить не менее 5 раз.

9. Рассчитать α_ср. и погрешность Δα:

,

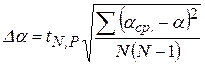где N – число опытов.

10. Сделать выводы.

Контрольные вопросы

1. Что та­кое ин­тер­фе­рен­ция волн?

2. Ка­кие исто­ч­ни­ки све­та на­зы­ва­ют­ся ко­ге­рент­ны­ми?

3. В чём состоит отличие интерференции от сложения некогерентных волн?

4. Почему невозможно осуществление двух когерентных источников обычного типа?

5. Какой метод используется в оптике для получения когерентных световых волн? Опишите метод Юнга и выведите формулу (1.11) для ширины интерференционной полосы.

6. Опи­шите ус­т­рой­ст­во би­приз­мы Фре­не­ля и объ­я­с­ните прин­цип ее дей­ст­вия.

7. По­че­му би­приз­му де­ла­ют с очень ма­лым пре­ло­м­ля­ю­щим уг­лом?

8. Вы­ве­с­ти фор­му­лу для оп­ре­де­ле­ния рас­сто­я­ния ме­ж­ду цен­т­ра­ми свет­лых ин­тер­фе­рен­ци­он­ных по­лос на эк­ра­не при ис­поль­зо­ва­нии би­приз­мы Фре­не­ля.