Принцип Гюйгенса-Френеля можна виразити: вторинні джерела, які еквівалентні джерелу S0 , когерентні між собою, тому вторинні, збуджені ними, інтерферують.

3 За допомогою принципу Гюйгенса-Френеля можна пояснити всі дифракційні явища, а також прямолінійне поширення світла. Метод зон Френеля полягає у тому, що фронт хвилі розбивають не на окремі точкові джерела (кожний фронт хвилі містить у собі нескінченну кількість таких джерел), а на певні ділянки – зони. Ширина зон визначається тим, що відстані від межі сусідніх зон до точки спостереження відрізняються на половину довжини хвилі. У зв’язку з цим коливання, що приходять у точку спостереження від аналогічних точок сусідніх зон, а водночас і результуючі коливання від цих зон, відрізнятимуться за фазою на величину π. Отже, внаслідок інтерференції ці коливання послаблятимуть одне одного.

Застосуємо метод зон Френеля для пояснення явища прямолінійного поширення світла в однорідному середовищі. Нехай S₀ – точкове джерело, М – довільна точка, в якій треба визначити амплітуду Е світлових коливань, S – положення фронту сферичної хвилі в певний момент часу. Побудуємо зони Френеля. Межею першої (центральної) зони Френеля є точки поверхні S, які містяться на відстані L+λ/2 від точки М (L – найкоротша відстань між точкою М і фронтом хвилі S). Точки сфери S, що лежать на відстані L+ 2λ/2, утворюють границю другої зони і т.д. зонами, дорівнюють відповідно Е₁, Е₂, ……….., то

Е = Е₁ - Е₂ + Е₃ – Е₄ + … .

При цьому можна покласти, що

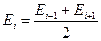
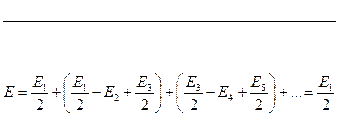
Формула показує, що результуюча дія в точці М повністю відкритого фронту світлових хвиль, що поширюється від джерела S₀, дорівнює половині дії однієї центральної зони. Як засвідчують математичні розрахунки, радіус цієї зони порівняно малий. Так, при S₀О = ОМ = 10 см і λ = 5 * 10^{-5 см r}₁ ≈ 0,016 см. Отже, з великою точністю можна вважати, що у вільному просторі світло від джерела S₀ у точку М поширюється прямолінійно.

4 Дифракція Фраунгофера спостерігається на нескінченності, тобто в паралельних променях. Часто для зручності спостереження використовують збиральну лінзу і дістають дифракційну картину у фокальній площині лінзи L. На рисунку Е – фронт падаючої плоскої хвилі; b – ширина отвору АВ в екрані К. Припустимо, що падаюче світло монохроматичне. Розглянемо дифракцію Фраунгофера на щілині з паралельними краями. Згідно з принципом Гюйгенса-Френеля всі точки щілини можна розглядати як джерела вторинних хвиль, що коливаються в одній фазі, оскільки площина щілини збігається з фронтом падаючої хвилі. Всі промені, що проходять крізь щілину в початковому напрямі, лінза збирає в одну лінію, яка проходить через точку О паралельно щілині.

Внаслідок дифракції світлові промені від щілини поширюється не лише в початковому напрямі, а й під різними кутами φ до цього напряму. Всі промені, що падають на лінзу L під кутом φ до її оптичної осі, збиратимуться в точці (лінії) Fφ, яка розташована у фокальній площині лінзи L. Різниця оптичного ходу хвиль Δ між крайніми променями, що йдуть від щілини в цьому напрямі, буде

Δ = ВС =b sin φ.

Щілину АВ можна розбити на зони Френеля. Ці зони матимуть вигляд однакових за шириною смуг, паралельних краям щілини.

Результуюча амплітуда в точці Fφ визначатиметься числом зон Френеля, на які розбито щілину для кута дифракції φ. Якщо число зон для цієї точки спостереження парне, то в ній спостерігатиметься дифракційний мінімум:

b sin φ = ± kλ / 2 (k = 1,2,3,…)

Знак мінус відповідає променям, які поширюються від щілини під кутом φ і збираються в точці (лінії), симетричній Fφ відносно головного фокуса 0.

Якщо число зон непарне, то спостерігатиметься дифракційний максимум, що відповідає дії однієї зони Френеля:

b sin φ = ± (2k + 1) λ / 2 (k = 1,2,3,…)

Число k називають порядком дифракційного максимуму (мінімуму). Отже, дифракційна картина, що утворюється від однієї щілини при освітленні її монохроматичним світлом, має вигляд світлих і темних смуг, які змінюють одна одну і розташовані симетрично по обидва боки від центральної світлої смуги.

Контрольні запитання

1 На якому принципі ґрунтується геометрична оптика?

2 Що таке дифракція?

3 Виразіть принцип Гюйгенса-Френеля.

4 У чому полягає метод зон Френеля?

5 Назвіть формули дифракційного мінімуму і максимуму.

Змістовий модуль 3.2Магнетизм. Магнітне поле електричного струму.