Задачи на пересечение

Задача на пересечение двух прямых рассмотрена ранее в разделе "Пересекающиеся прямые". Наиболее важной позиционной задачей является задача о пересечении прямой с плоскостью. При решении задачи могут встретиться следующие случаи пересечения:

1. Прямая общего положения пересекается с плоскостью частного положения;

2. Прямая частного положения (например, проецирующая) пересекается с плоскостью общего положения;

3. Прямая общего положения пересекается с плоскостью общего положения.

Решение первых двух задач не представляет особых трудностей (рисунок 4.7). На рисунке4.7а дано построение точки встречи прямой общего положения с горизонтально-проецирующей плоскостью, а на рисунке 4.7б– горизонтально-проецирующей прямой с плоскостью общего положения. Последняя задача решена с помощью вспомогательной прямой 1-2.

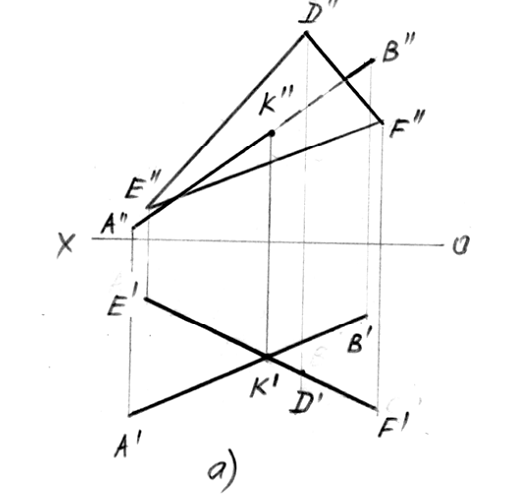
Рисунок 4.7 – Пересечение прямой с плоскостью

Для решения задачи о пересечении прямой с плоскостью в общем положении разработана следующая методика (рисунок 4.8а):

1) Через прямую проводят вспомогательную плоскость частного положения β(чаще всего проецирующую плоскость, заданную следами);

2) Находят линию пересечения заданной α и вспомогательной плоскостей β(линия1-2);

3) Находят точку пересечения заданной прямой и найденной линии пересечения плоскостей. Полученная точка K– искомая.

Рисунок4.8 – Пересечение прямой общего положения с плоскостью

общего положения

На рисунке4.8б дана пространственная схема решения задачи, в которой прямая пересекается с плоскостью, заданной следами. В качестве вспомогательной плоскости взята горизонтально-проецирующая плоскость. На рисунке4.9 дано решение задачи на пересечение прямой общего

положения с плоскостью общего положения, заданной треугольником. В качестве вспомогательной плоскости использована горизонтально-проецирующая плоскость. Видимость проекций определена методом конкурирующих точек (прямых).

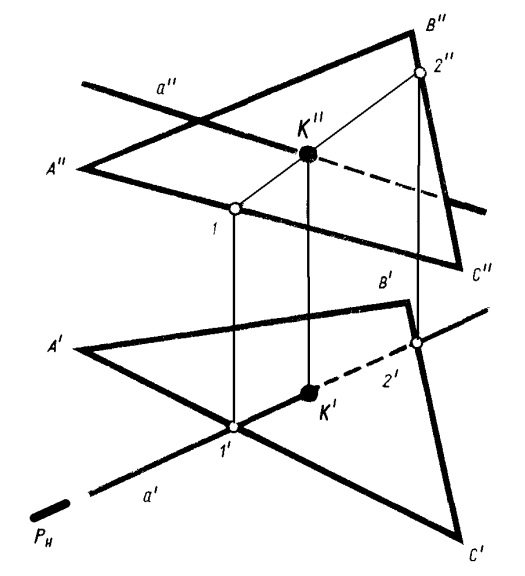
Рисунок4.9 – Задача на пересечение прямой с плоскостью

К главным задачам на пересечение относится также задача о пересечении двух плоскостей. Линия пересечения двух плоскостей– это прямая, принадлежащая как одной, так и другой плоскости. Следовательно, для построения линии пересечения двух плоскостей надо найти какие-либо две точки, каждая из которых принадлежит обеим плоскостям (рисунок4.10).

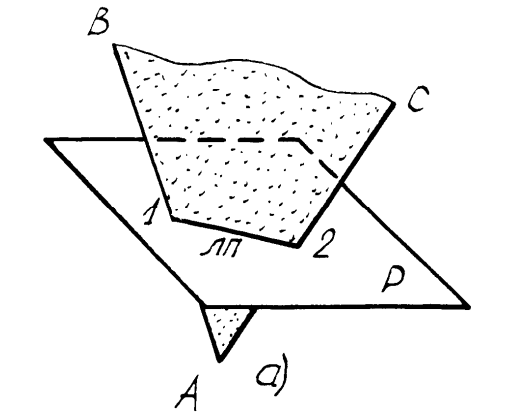
Рисунок4.10 – Линия пересечения двух плоскостей

Если плоскости заданы следами, то исходя из рисунка4.10б линия пересечения таких плоскостей определяется точками пересечения одноименных следов. На рисунке4.11 представлены решения задач о пересечении двух плоскостей, заданных следами. Во втором случае одна из плоскостей является плоскостью общего положения, а другая– фронтально-проецирующей.

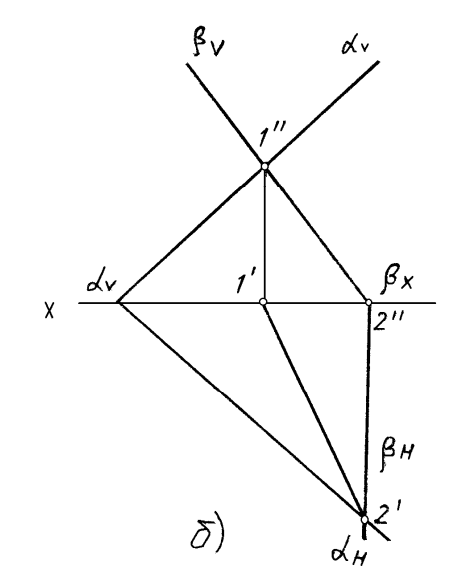
Рисунок4.11 – Пересечение плоскостей, заданных следами

В случаях, если плоскости заданы разными способами, применяют общий метод построения линии пересечения, основанный на введении

вспомогательных плоскостей(рисунок4.12). Сущность метода заключается в том, что заданные плоскости Q и P дважды пересекают вспомогательными плоскостями α и β(например, горизонтальными). Находят линии их пересечения с заданными плоскостями, далее находят точки 1 и 2 пересечения найденных линий и соединяют полученные точки прямой линией, которая является линией пересечения заданных плоскостей.

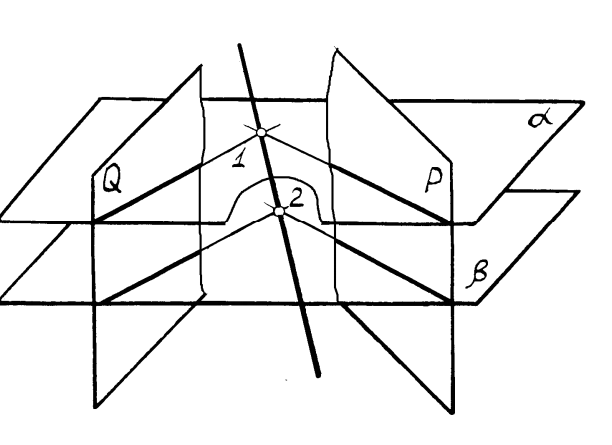
Рисунок4.12 – Введение вспомогательных секущих плоскостей

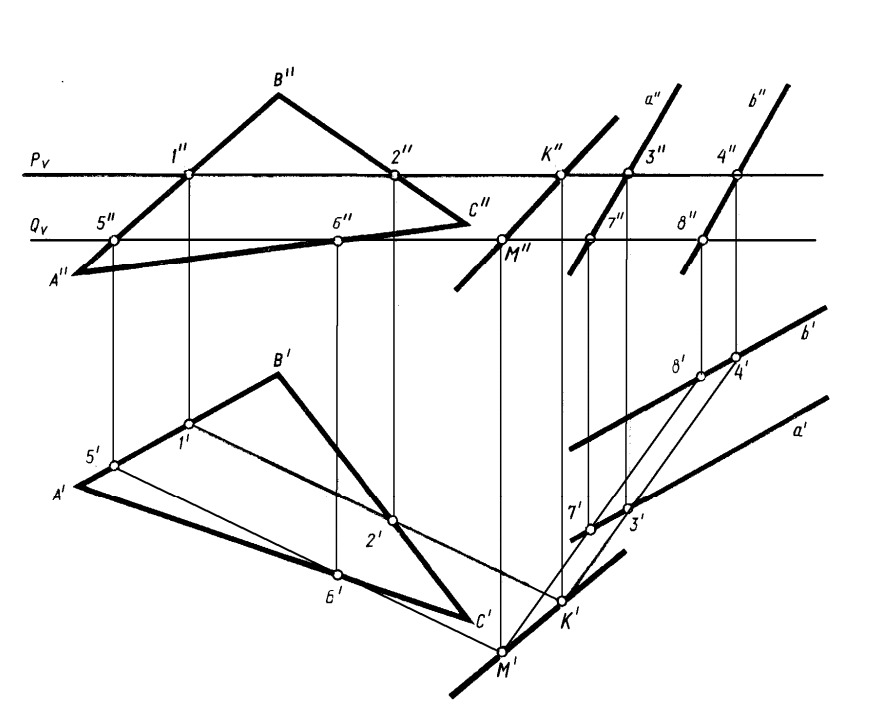
Рисунок4.13 – Пример на пересечение двух плоскостей

Если пересекающиеся плоскости являются плоскостями частного положения, или если одна из пересекающихся плоскостей является плоскостью частного положения, то задача упрощается. На рисунке 4.14 представлены примеры решения задач на пересечение упомянутых плоскостей.

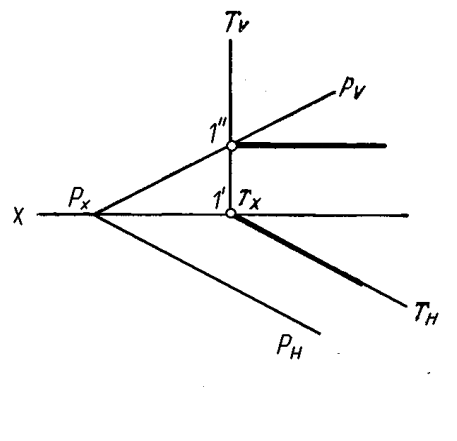
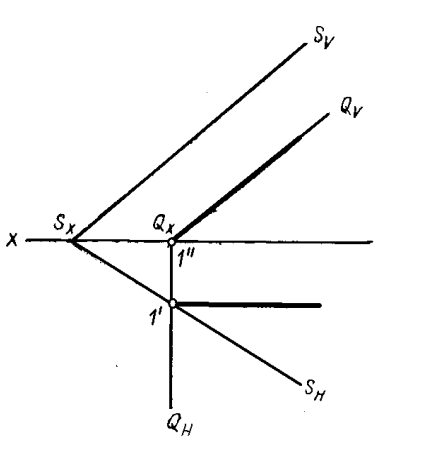
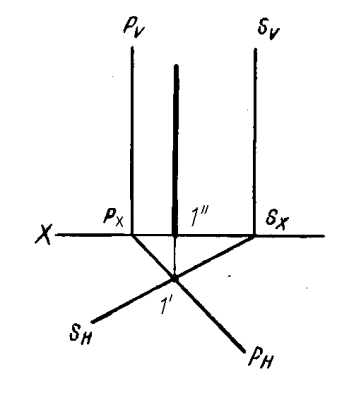
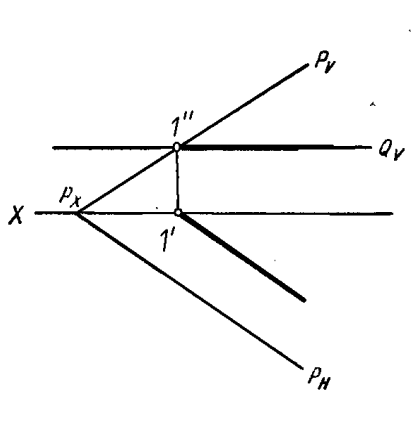
Рисунок 4.14

Наиболее трудоемкой задачей является задача на пересечение двух

плоскостей общего положения, заданных плоскими фигурами, например, треугольниками, многоугольниками и т.д. При пересечении плоских фигур возможны два случая пересечения (рисунок4.15): полное пересечение(а) и неполное пересечение(б).

4.3 Задачи на параллельность

Задача на параллельность двух прямых была рассмотрена ранее в разделе"Параллельные прямые". Задачи на параллельность плоскостей основываются на положениях элементарной геометрии. Две плоскости параллельны, если две пересекающиеся прямые одной плоскости взаимно параллельны двумпересекающимся прямым другой плоскости(рисунок4.16а).

Если две параллельные плоскости заданы следами, то одноименные следы таких плоскостей параллельны друг другу(рисунок4.16б). Прямая будет параллельна плоскости в том случае, если она параллельна любой прямой, находящейся в этой плоскости.

Рисунок4.16 – Параллельность геометрических объектов

ПРИМЕР4.1. Через прямую AB провести профильно-проецирующую плоскость(рисунок4.17).

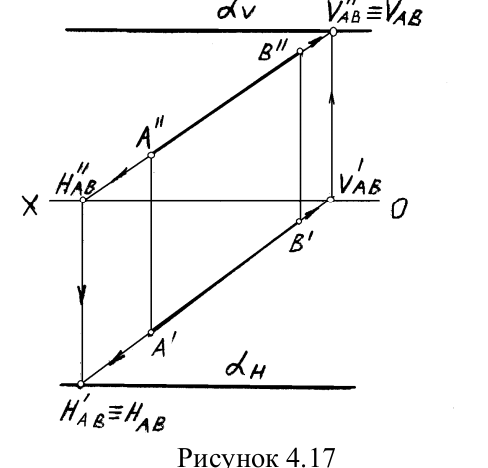
РЕШЕНИЕ. Как было показано ранее горизонтальный и фронтальный следы профильно-проецирующей плоскости располагаются параллельно оси0X. Было также показано, что если прямая принадлежит плоскости, заданной следами, то следы прямой находятся на одноименных следах плоскости. Сказанное позволяет разработать план решения задачи:

1) Найдем горизонтальный и фронтальный следы прямой;

2) Через найденные следы прямой проведем одноименные следы плоскости.

ПРИМЕР4.2. Через точку провести плоскость, параллельную заданной(рисунок4.18).

РЕШЕНИЕ. Плоскость задана следами. Искомую плоскость целесообразно тоже задать следами. Чтобы обеспечить параллельность плоскостей, необходимо следы искомой плоскости провести параллельно одноименным следам заданной плоскости. Для того чтобы искомая плоскость проходила через заданную точку, необходимо через точку провести прямую(например, горизонталь), которая принадлежала бы искомой плоскости. Исходя из изложенного, определяется следующий план решения задачи:

1) Проводим через заданную точку горизонталь h;

2) Через фронтальный след горизонтали проводим фронтальный след

искомой плоскости параллельно фронтальному следу заданной плоскости;

3) Горизонтальный след искомой плоскости проводим параллельно

горизонтальному следу заданной плоскости.

ПРИМЕР4.3. Построить линию пересечения треугольников ABC и EDK, определить видимость проекций (рисунок4.19).

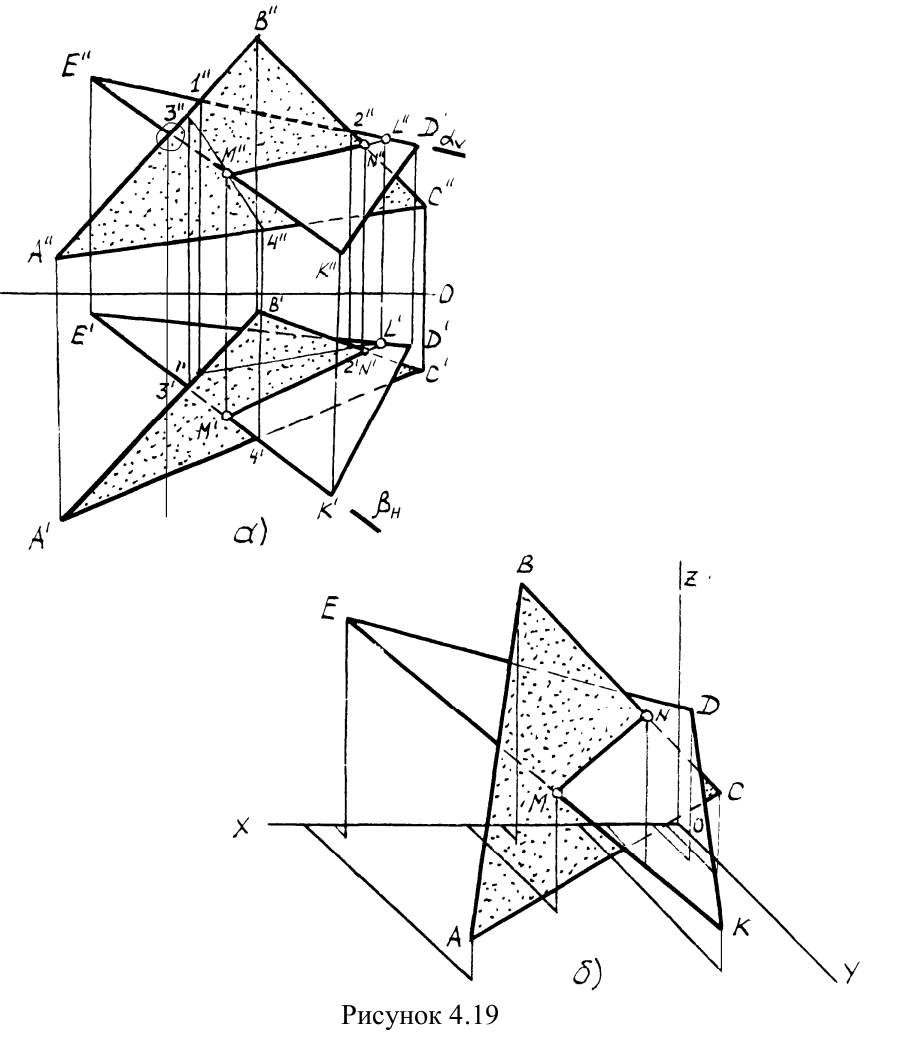
РЕШЕНИЕ. Предварительно намечаем две произвольные задачи на пересечение стороны одного треугольника с плоскостью другого (произвольно). Например, ED Ι ΔABC, EK Ι ΔABC. Решаем первую задачу. Через ED проводим вспомогательную фронтально-проецирующую плоскость α(след плоскости αV). Она пересекает треугольник ABC в двух точках1 // ,2 // на сторонах AB и BC. Находим горизонтальные проекции этих точек1 // и2 // и соединяем их.

Линия1-2 является линией пересечения вспомогательной плоскости с плоскостью треугольника ABC. Ищем точку пересечения линии1-2 с прямой ED. Это точка L / , которая лежит вне треугольника ABC, но является точкой линии пересечения треугольников. Аналогично решаем вторую задачу. В качестве вспомогательной плоскости берем горизонтально-проецирующую плоскость β(след βV). В результате решения задачи получаем точку M. Далее соединяем полученные точки L и M. Однако не вся эта линия будет являться линией пересечения треугольников, а лишь участок MN, который принадлежит обоим треугольникам. Таким образом, в результате решения двух произвольно выбранных задач получили линию MN пересечения заданных треугольников. Определяем видимость проекций треугольников. При определении видимости проекций методом конкурирующих точек(прямых) необходимо учитывать следующие особенности:

1) Плоскости треугольников считаются геометрически непрозрачными;

2) В точках M и N линии пересечения видимость сторон треугольников меняется;

3) Если при вершине какого-либо треугольника одна сторона видна (не видна), то и другая сторона будет видна(не видна).

Учет перечисленных особенностей позволяет определить видимость проекций треугольников по анализу одного конкурирующего места на каждой проекции, что значительно ускоряет решение задачи. Отметим на фронтальной проекции любое конкурирующее место из шести(отмечено кружочком). Проведем через него линию связи и вдоль линии связи сравним ординаты конкурирующих прямых EK и AB. Наибольшую ординату имеет прямая AB. Она и будет видна на рассматриваемой фронтальной проекции. Видимость остальных сторон треугольников определяется с учетом особенностей, отмеченных выше. На горизонтальной проекции отметим конкурирующее место, в котором конкурируют прямые AB и ED. Аналогично описанному определяем, что на горизонтальной проекции будет видна прямая AB, так как у ней наибольшая аппликата. Видимость остальных сторон треугольников определим аналогично рассмотренному выше. Для усиления эффекта видимости треугольников на проекциях целесообразно один их треугольников заштриховать с учетом видимости или раскрасить оба треугольника. На рисунке4.19б представлено наглядное аксонометрическое изображение пересекающихся треугольников в косоугольной фронтальной изометрии. Вершины треугольников строятся по заданным координатам точек, линия пересечения MN– по координатам, взятым с проекционного чертежа.

МЕТРИЧЕСКИЕ ЗАДАЧИ

Метрические задачи– это задачи на определение линейных или угловых размеров геометрических объектов, а также расстояний и углов между ними.

Главным вопросом метрических задач является вопрос о построении перпендикуляра к прямой или плоскости. Построение взаимно перпендикулярных прямых было рассмотрено ранее.

Из элементарной геометрии известно, что прямая перпендикулярна к плоскости, если она перпендикулярна двум пересекающимся прямым, принадлежащим этой плоскости. В качестве этих пересекающихся прямых наиболее целесообразно использовать горизонталь и фронталь плоскости.

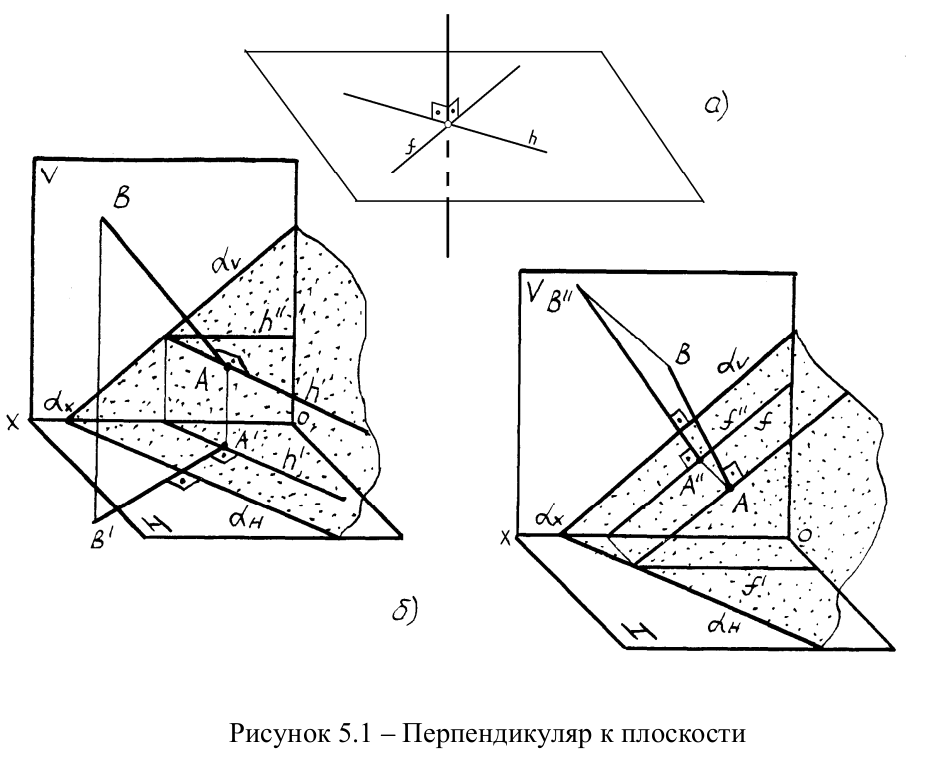
Это объясняется тем, что только в этом случае прямой угол будет проецироваться в натуральную величину на соответствующие плоскости проекций. На рисунке5.1 приведен пространственный чертеж, на котором из плоскости α(из точки A) восстановлен перпендикуляр AB. Из приведенного изображения можно выяснить методику построения проекций перпендикуляра к плоскости: горизонтальная проекция перпендикуляра к плоскости проводится перпендикулярно горизонтальной проекции горизонтали или горизонтальному следу плоскости, а фронтальная проекция перпендикуляра проводится перпендикулярно

фронтальной проекции фронтали или фронтальному следу плоскости.

Таким образом, необходимо выполнить следующий алгоритм проведения

проекций перпендикуляра к плоскости:

если AB ⊥ α, то A/B/⊥h/ или αH; A//B//⊥f// или αV.

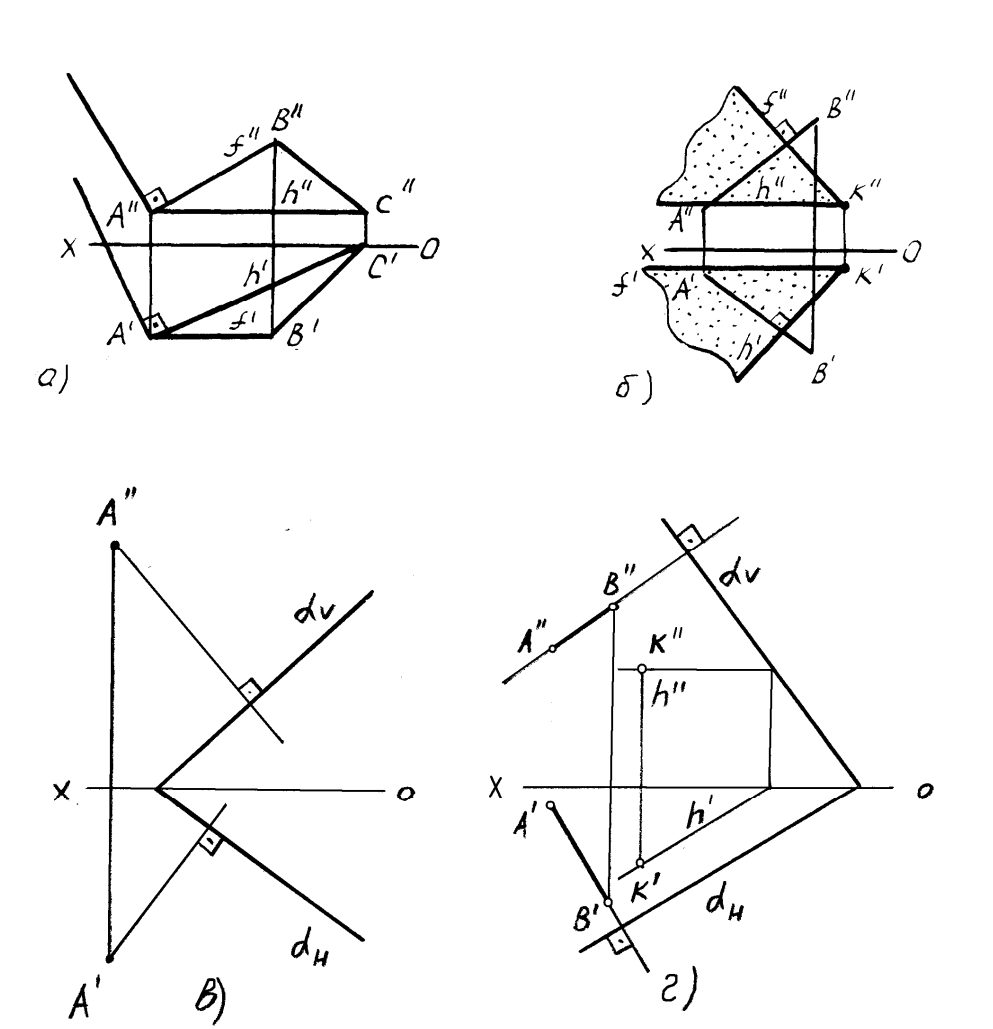
Построение перпендикуляра к плоскость и восстановление перпендикуляра из плоскости называется прямой задачей, а построение плоскости, перпендикулярной к прямой– обратной задачей. Обе задачи решаются по одному и тому же вышеописанному алгоритму. При этом плоскость, перпендикулярную заданной прямой, можно задать следами или пересекающимися горизонталью и фронталью. На рисунке5.2 показано решение прямой(а) и обратной(б) задач. В прямой задаче из точки A треугольника ABC восстановлен перпендикуляр, в обратной задаче через точку K проведена плоскость, перпендикулярная прямой AB. Плоскость задана пересекающимися горизонталью и фронталью.

Здесь же приведены примеры прямой и обратной задач, если плоскость задана следами. В прямой задаче(в) из точки А построен перпендикуляр на плоскость, в обратной(г) – через точкуK проведе на плоскость перпендикулярно прямой AB.

5.1 Определение расстояний между геометрическими объектами Среди этих задач можно выделить следующие задачи: расстояние от точки до плоскости, расстояние от точки до прямой, расстояние между двумя параллельными прямыми, расстояние между двумя скрещивающимися прямыми, расстояние между двумя параллельными плоскостями и другие. В общем случае все задачи сводятся к определению расстояний между двумя точками. Чтобы определить расстояние от точки до плоскости, необходимо выполнить ряд логических действий:

1) Из точки опустить перпендикуляр на заданную плоскость;

2) Найти точку встречи перпендикуляра с плоскостью;

3) Определить НВ расстояния между заданной и найденной точками.

Задача на определение расстояния от точки до прямой решается по

следующему плану:

1) Через точку k провести плоскость, перпендикулярную заданной прямой;

2) Найти точку встречи M заданной прямой с проведенной плоскостью;

3) Соединить полученные точки(это будет перпендикуляр из точки на прямую);

4) Определить НВ перпендикуляра.

Пространственная модель решения второй задачи представлена на

рисунке5.3. Рассмотренная задача относится также к задачам на

перпендикулярность двух прямых.

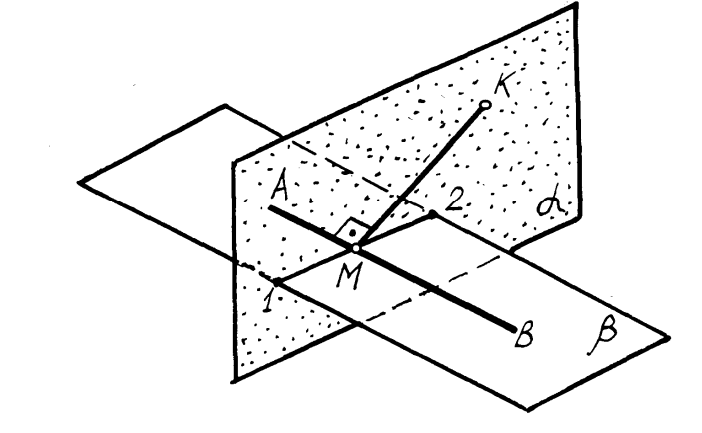
Рисунок 5.3 – Расстояние от точки до прямой

Другие упомянутые задачи на определение расстояний легче

решаются методами преобразования эпюра, которые будут рассмотрены в

последующих разделах.

5.2 Перпендикулярность плоскостей

Плоскость перпендикулярна другой плоскости, если она содержит прямую, перпендикулярную другой плоскости(рисунок5.4а). Таким образом, для того, чтобы провести плоскость, перпендикулярную другой, необходимо сначала провести перпендикуляр к заданной плоскости, а затем через него провести искомую плоскость. На рисунке 5.4б представлена задача: через точку K провести плоскость, перпендикулярную плоскости треугольника ABC. Искомая плоскость задана двумя пересекающимися прямыми, одна из которых перпендикулярна заданной плоскости. Если две плоскости являются одноименными плоскостями частного положения(например, горизонтально- или фронтально-проецирующими), то при перпендикулярности плоскостей их собирательные следы будут перпендикулярны друг другу(рисунок 5.4в,г).

Если плоскости являются плоскостями общего положения, то при их перпендикулярности одноименные следы не будут взаимно перпендикулярны. Другими словами, перпендикулярность одноименных следов плоскостей общего положения не является достаточным условием для перпендикулярности самих плоскостей.

5.3 Определение углов между прямой и плоскостью и между двумя

плоскостями.

Определение углов между геометрическими объектами является трудоемкой задачей, если её решать традиционными геометрическими способами. Так, например, задачу на определение угла между прямой и плоскостью(рисунок5.5) можно решить способом, алгоритм которого содержит следующие операции:

1) Определить точку встречи прямой AB с плоскостью α;

2) Из точки B построить перпендикуляр на плоскость;

3) Найти точку встречи перпендикуляра с плоскостью;

4) Точки K и N соединить и определить НВ угла BKN.

Однако задача может быть значительно упрощена, если использовать

способ решения задачи с помощью дополнительного угла.

Дополнительным углом назовем угол между заданной прямой AB и

перпендикуляром BN, обозначенный через Θ ο

. Из приведенного рисунка видно, что, если из точки B прямой построить на плоскость перпендикуляр, определить НВ дополнительного угла Θο , то искомый угол определится по формуле:

ϕο= 90ο− Θο,

которую можно решить графически, достроив угол Θ до90ο. То же самое можно сказать о задаче на определение двугранногоугла, то есть угла между двумя плоскостями(рисунок5.6б). Первый способ(геометрический) достаточно трудоемок. Он заключается в пересечении угла вспомогательной плоскостью α, перпендикулярной ребру AB, построении линий пересечения KN и KL и определении натуральной величины угла NKL. Рисунок5.6 – Угол между двумя плоскостями С помощью дополнительного угла задача решается следующим образом. В растворе двугранного угла(рисунок5.6в) берут любую точку K и строят из неё перпендикуляры на обе плоскости двугранного угла, которые образуют дополнительный угол Θο . Далее определяют НВ дополнительного угла и дополняют его(графически) до180 градусов, исходя из формулы:

ϕο= 180ο− Θο,

Дополненный угол будет искомым.

Натуральную величину дополнительного угла Θο в обеих задачах наиболее целесообразно определять методом вращения вокруг горизонтали или фронтали, который будет изложен в последующих темах.

ПРИМЕР 5.1. Из любой вершины треугольника ABC восстановить перпендикуляр длиной40 мм.

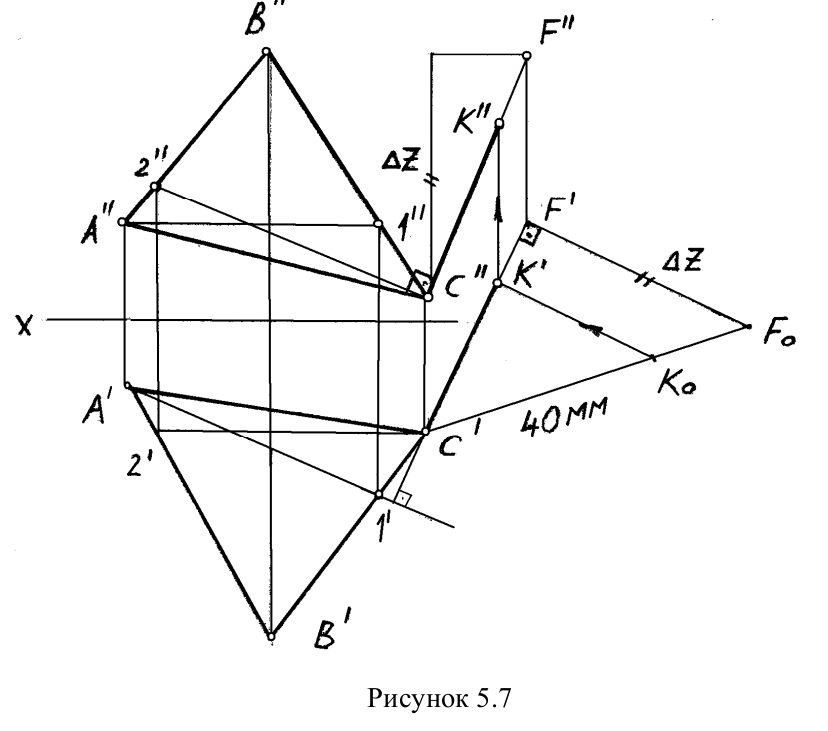
РЕШЕНИЕ. Сначала необходимо в плоскости треугольника ABC

провести горизонталь и фронталь для того, чтобы построить проекции восстановленного перпендикуляра. Далее из точки С проводим проекции перпендикуляра согласно рассмотренному выше алгоритму о перпендикуляре к плоскости. Для того, чтобы отложить40 мм, необходимо определить НВ ограниченного отрезка перпендикуляра CF(точку F берем произвольно). НВ отрезка CF определяем методом прямоугольного треугольника на горизонтальной проекции CF. Полученную точку К возвращаем на проекции по теореме Фалеса. Получаем проекции перпендикуляра длиной40 мм (рисунок. 5.7).

ПРИМЕР 5.2. Найти расстояние от точки А до плоскости, заданной

следами.

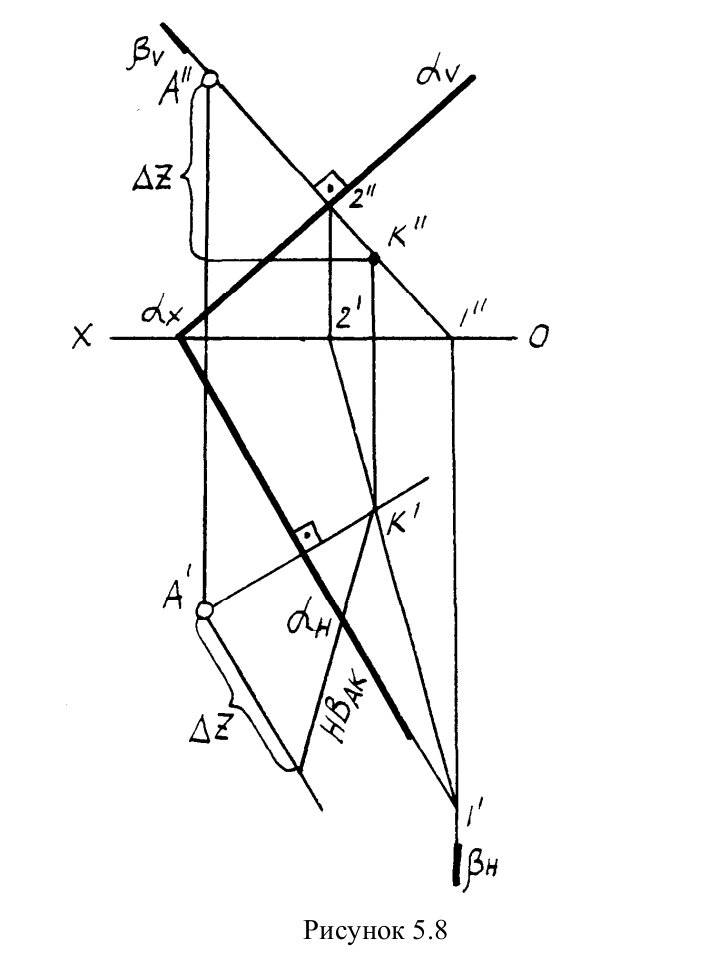
РЕШЕНИЕ. Из точки А строим перпендикуляр на заданную плоскость. Проекции перпендикуляра проводим перпендикулярно следам. Далее находим точку встречи перпендикуляра с заданной плоскостью с помощью вспомогательной фронтально-проецирующей плоскости β. Находим линию пересечения плоскостей α и β(линия1-2) и точку встречи K/ в месте пересечения горизонтальной проекции перпендикуляра с линией1-2. Методом прямоугольного треугольника определяем НВ расстояния AK(рисунок5.8).

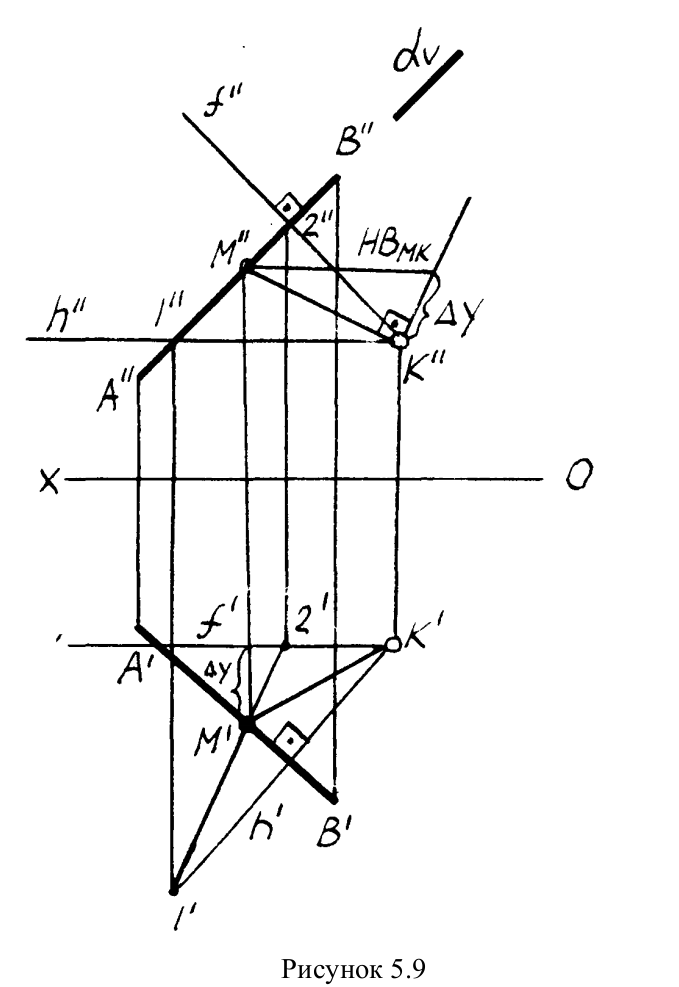
ПРИМЕР 5.3. Определить расстояние от точки K до прямой AB.

РЕШЕНИЕ. Через точку K проводим плоскость, перпендикулярную заданной прямой. Плоскость задаем пересекающимися горизонталью и фронталью. Их проекции проводим согласно алгоритму о перпендикуляре к плоскости(обратная задача). Далее находим точку встречи прямой AB с проведенной плоскостью(точка M). Определяем натуральную величину KM методом прямоугольного треугольника (рисунок5.9).