Задачи на принадлежность

Лекция 4 ПОЗИЦИОННЫЕ ЗАДАЧИ

Позиционными задачами называются задачи на построение элементов, общих для взаимодействующих объектов, и задачи на взаимное положение геометрических объектов. Первая группа задач включает задачи на принадлежность и задачи на пересечение. Ко второй группе задач относятся задачи на параллельность геометрических объектов.

Задачи на перпендикулярность объектов относят к метрическим задачам, которые будут рассмотрены в следующем разделе.

Классификация позиционных задач, относящихся к элементарным геометрическим объектам(точка, прямая, плоскость), представлена на рисунке 4.1.

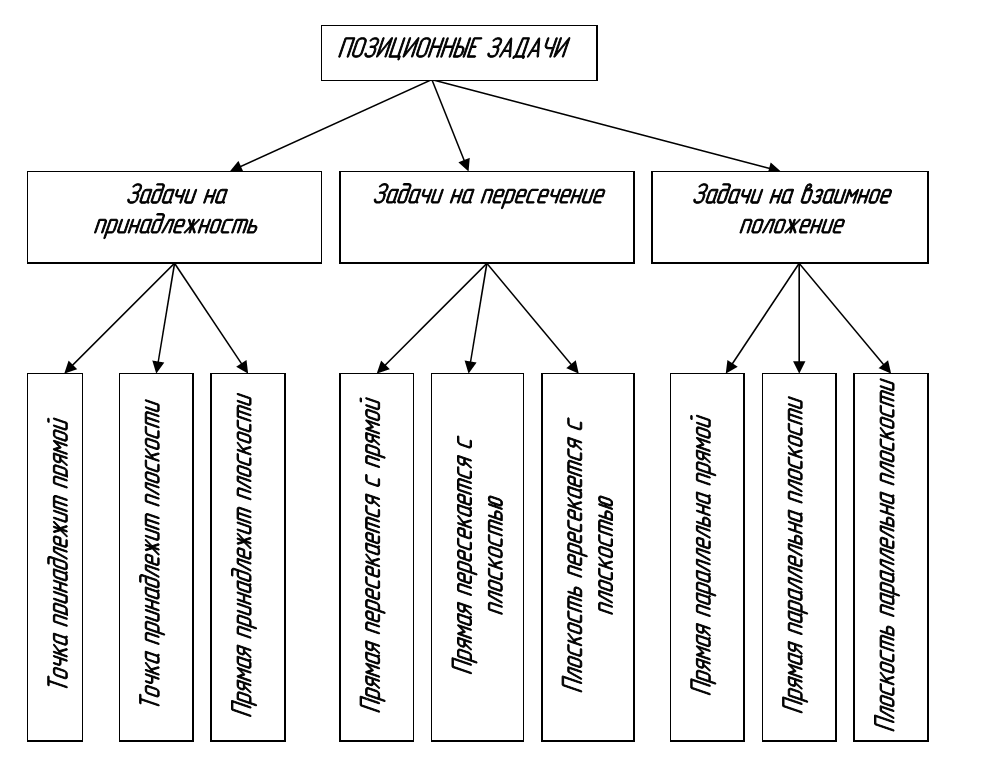
Рисунок4.1 – Классификация позиционных задач

Задачи на принадлежность

Эта группа задач содержит три типовые задачи – точка принадлежит прямой, точка принадлежит плоскости, прямая принадлежит плоскости, суть решения которых основана на свойствах проецирования. Если точка принадлежит прямой, то проекции этой точки принадлежат одноименным проекциям прямой.

Рисунок 4.2 – точка и прямая в плоскости

Точка принадлежит плоскости, если она принадлежит прямой, находящейся в этой плоскости (рисунок4.2а). Прямая принадлежит плоскости, если она проходит через две точки, принадлежащих плоскости. Поэтому для того, чтобы указать в плоскости какую-либо точку, необходимо сначала указать в плоскости прямую, а затем на этой прямой указать положение точки.

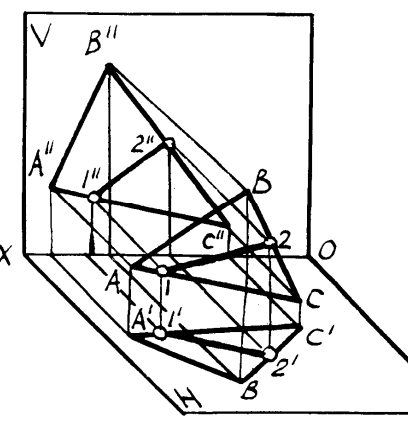
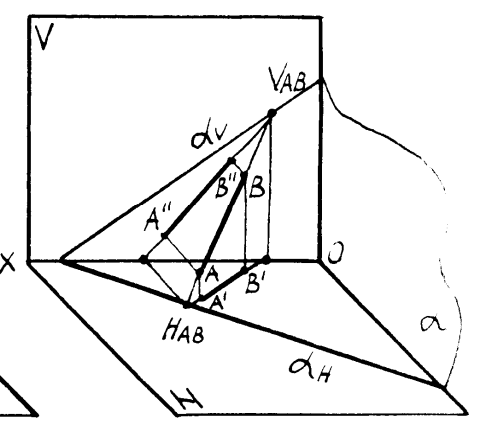
Рисунок4.3 –Построение прямой в плоскости

На рисунках4.3 показано построение прямой в плоскостях, заданных треугольником и следами. Если плоскость задана треугольником, то целесообразно упомянутые точки взять на сторонах треугольника. Если плоскость задана следами, то в качестве двух точек целесообразно взять следы прямой. Это основано на следующем свойстве: если плоскость задана следами и в ней находится прямая, то следы прямой лежат на одноименных следах плоскости. На рисунке 4.4 представлено построение точек в плоскости, заданной следами и точки в плоскости, заданной треугольником. В первом случае точка A построена с помощью горизонтали. На этом же рисунке показано построение точек(K и L), находящихся на следах плоскости. Во втором случае точка K построена с помощью прямой 1-2. С рассматриваемым вопросом тесно связан вопрос о проведении плоскости частного положения (например, проецирующих плоскостей) через прямую. Если прямая принадлежит плоскости частного положения и плоскость задается следами, то одна из проекций прямой будет совпадать с собирательным следом плоскости в соответствие с рисунком 4.5. На рисунке4.6 в эпюрной форме показано проведение через прямую фронтально проецирующей плоскостиα и горизонтально проецирующей плоскости β.

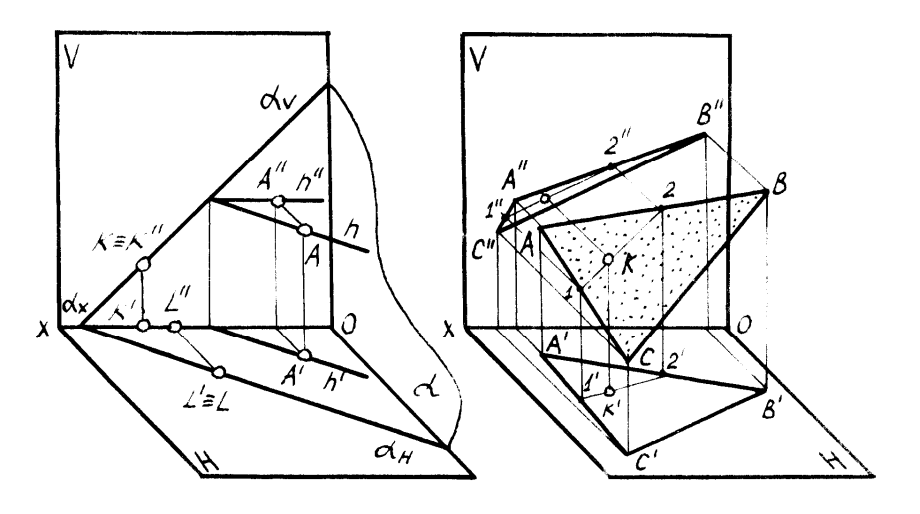
Рисунок4.4 – Построение точек в плоскости

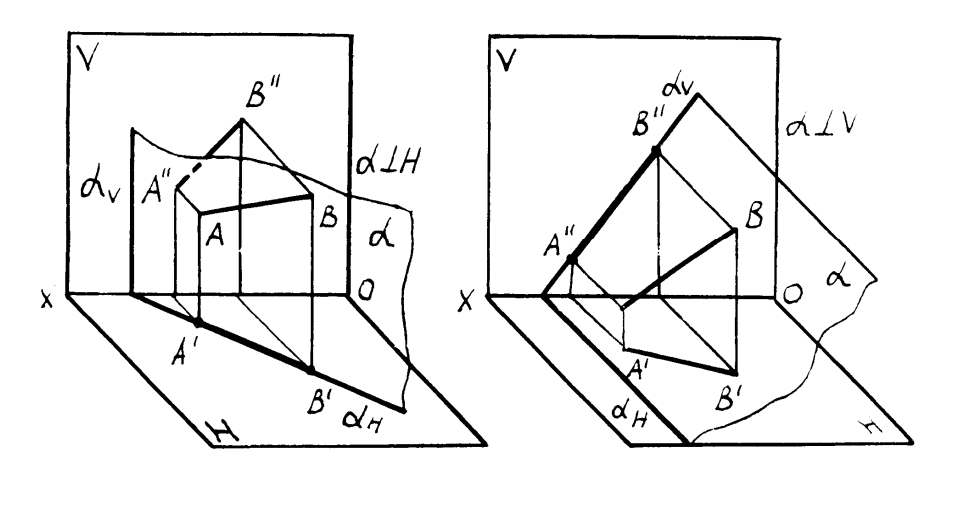
Рисунок4.5 –Построение проецирующей плоскости через прямую

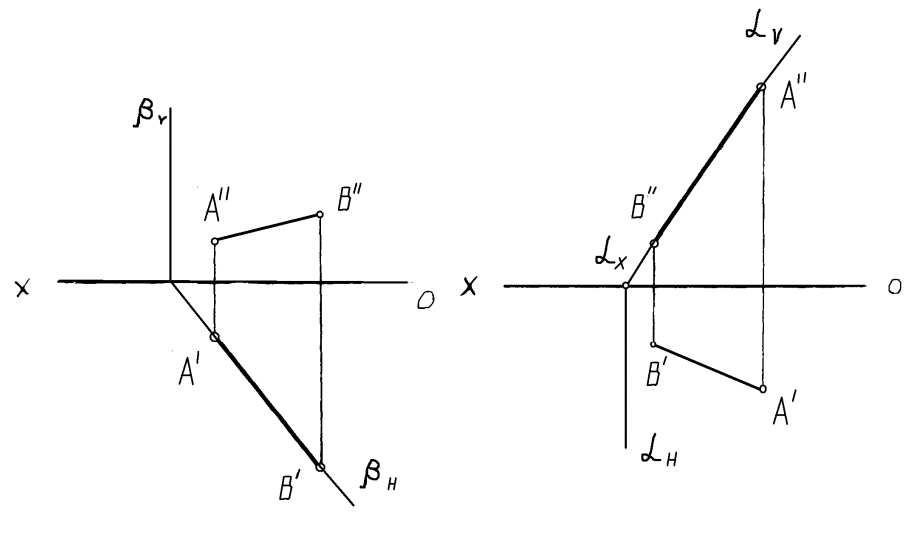
Рисунок4.6 - Построение проецирующей плоскости через прямую