Схема Эйткина

Пусть требуется найти не общее выражение 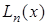, а лишь его значения при конкретных x. При этом, значения функции даны в достаточно большом количестве узлов, тогда удобно пользоваться интерполяционной схемой Эйткина. Согласно этой схеме последовательно вычисляются многочлены:

.

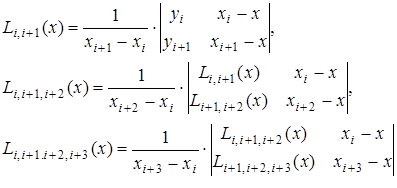Интерполяционный многочлен степени «n», принимающий в точках xiзначения 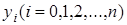, запишется следующим образом:

.

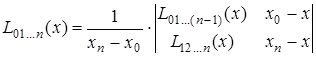Вычисления по схеме Эйткина удобно расположить в такой таблице:

Таблица 5.4.

Вычисления по схеме Эйткина

						…
						…

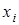
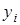
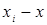
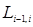
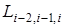
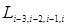
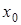
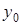
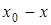
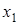
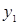
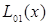
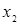
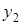
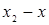
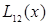
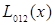
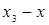
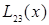
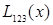
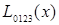
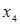
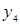
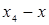
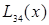
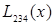
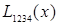
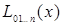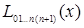Вычисления по схеме Эйткина обычно ведут до тех пор, пока последовательные многочлены и в таблице 5.4 не совпадут в пределах заданной точности.

Пример 5.5 Функция 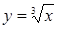задана таблицей

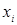
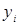
1.0	1.000
1.1	1.032
1.3	1.091
1.5	1.145
1.6	1.170

Применяя схему Эйткина, найти 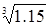Составим таблицу 5.4 для примера:

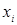
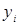
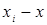
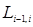
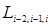
1.0	1.000	-0.15
1.1	1.032	-0.05	1.048
1.3	1.091	0.15	1.047	1.048
1.5	1.145	0.35	1.050
1.6	1.170	0.45	1.057

Значения 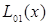и 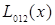совпадают до третьего знака. На этом вычисления можно прекратить и с точностью до 0.001 записать 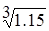=1.048