Метод релаксаций
Пусть дана система: (3.1)
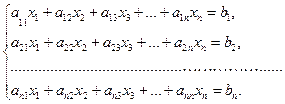
Преобразуем эту систему следующим образом: перенесем свободные члены налево и разделим первое уравнение на 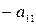 , второе – на
, второе – на 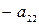 и т.д. Тогда получим систему, приготовленную к релаксации:
и т.д. Тогда получим систему, приготовленную к релаксации: 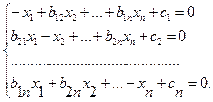 , где
, где 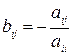
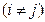 и
и 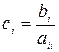 .
.
Пусть 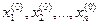 - начальное приближение решения системы. Подставляя эти значения в систему, получим в правых частях уравнений системы некоторые числовые значения . Будем называть их невязками. Невязки обращаются в нуль при подстановке корней в уравнения системы
- начальное приближение решения системы. Подставляя эти значения в систему, получим в правых частях уравнений системы некоторые числовые значения . Будем называть их невязками. Невязки обращаются в нуль при подстановке корней в уравнения системы
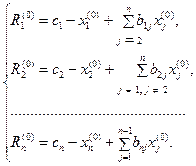 .
.
Если одной из неизвестных 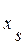 дать приращение
дать приращение 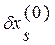 , то соответствующая невязка
, то соответствующая невязка 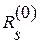 уменьшится на величину
уменьшится на величину 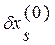 , а все остальные невязки
, а все остальные невязки 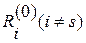 увеличатся на величину
увеличатся на величину 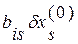 . Таким образом, чтобы обратить очередную невязку
. Таким образом, чтобы обратить очередную невязку 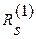 в нуль, достаточно величине
в нуль, достаточно величине 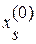 дать приращение
дать приращение 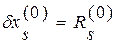 и мы будем иметь
и мы будем иметь 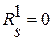 и
и 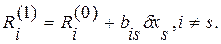
Суть метода заключается в том, чтобы на каждом шаге обращать в нуль максимальную по модулю невязку, изменяя значения соответствующей компоненты приближения. Процесс заканчивается, когда все невязки преобразованной системы будут равны нулю с заданной степенью точности.
Пример3.1: Пусть дана линейная система. Решить с точностью 0.01.
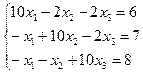 .
.
Приведем систему к виду, удобному для релаксации:
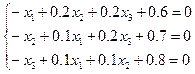 .
.
Выбирая в качестве начальных приближений корней нулевые значения 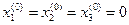 , находим
, находим 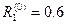 ,
, 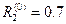 ,
, 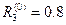 .
.
Согласно общей теории полагаем: 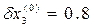 . Отсюда получаем невязки
. Отсюда получаем невязки
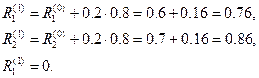
Далее полагаем 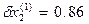
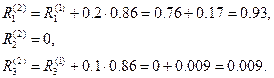
Суммируя все приращения 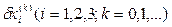 получим значения корней:
получим значения корней:
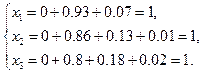
Удобно располагать вычисления в таблице:
| x1 | R1 | x2 | R2 | x3 | R3 |
| 0.93 | .60 0.16 | 0.86 | 0.70 0.16 | 0,80 0.18 | 0.80 -0.80 |
| 0.76 0.17 | 0.86 -0.86 | 0.09 | |||
| 0.93 -0.93 | 0.13 | 0.09 | 0.09 0.09 | ||
| 0.07 | 0.04 | 0.09 0.04 | 0.18 -0.18 | ||
| 0.04 0.03 | 0.13 -0.13 | 0.02 | 0.01 | ||
| 0.07 -0.07 | 0.01 | 0.01 | 0.01 0.01 | ||
| 0.01 | 0.02 -0.02 | ||||
| 0.01 -0.01 | |||||
| 1.00 | 1.00 | 1.00 |
Ответ: 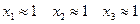
Дата добавления: 2015-10-09; просмотров: 681;
