Оценка погрешности приближений процесса итераций

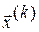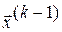Пусть и - два последовательных приближения системы (3.2). Тогда для приближения 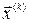справедлива оценка

:,

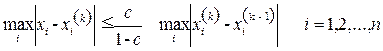если выполнено первое условие теоремы 3.1, или

,

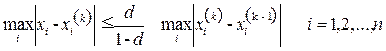если выполнено второе условие теоремы 3.1. Процесс итерации заканчивают, когда указанные оценки свидетельствуют о достижении заданной точности ε.

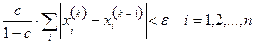
или

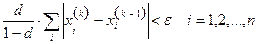
3.1.2. Приведение линейной системы к виду, удобному для итерации:

Сходимость накладывает жесткие условия на коэффициенты данной линейной системы 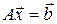. Однако, если 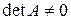, то с помощью линейного комбинирования уравнений системы, последнюю всегда можно заменить эквивалентной системой 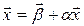, такой, что условия сходимости будут выполнены. Умножим уравнение (3.1) на матрицу 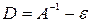, где 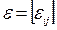- матрица с малыми по модулю, одинаковыми элементами. Тогда будем иметь:

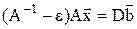
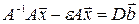
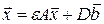
или 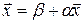, где и .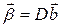

Все элементы матрицы ε выбираем одинаковыми из условия 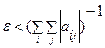. Это обеспечивает выполнение достаточного условия сходимости метода.

Пример 3.1 Решить систему методом итераций в Mathcad с тремя верными цифрами после запятой

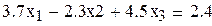
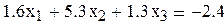
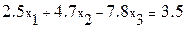
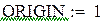
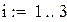
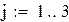
Точность вычислений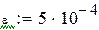

Решение исходной системы матричным методом

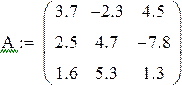
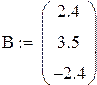
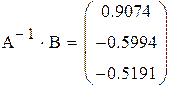
Линейными преобразованиями добиваемся диагонального преобладания.

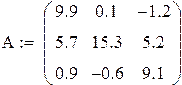
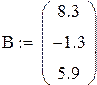
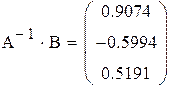
Преобразуем к виду, удобному для итераций.

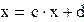
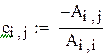
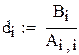
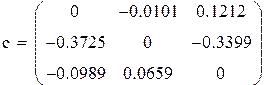
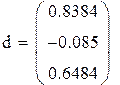
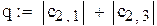
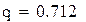
q-это норма матрицы «с»

В качестве начального приближения возьмем столбец свободных членов, сделаем 6 приближений, вектор разностей между соседними приближениями обозначим z. Результаты поместим в матрицу x.

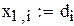
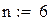
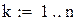
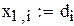
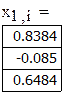
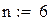
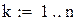
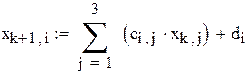
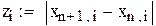
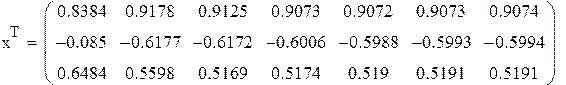
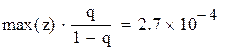
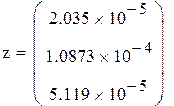
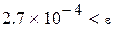
Ответ: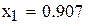

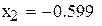
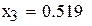
Рис. 3.1.Решение примера 3.1 в Mathcad