Изоморфизм и гомеоморфизм графов

Определение. Удалением вершины v из графа G = (V, X) называется операция, при которой из множества V удаляется элемент v, а из Х — все ребра, содержащие v. Удалением ребра х из графа G = (V, X) называется удаление элемента х из множества Х.

Подразбиением ребра х называется операция, состоящая из: 1) удаления ребра х = (v, w), 2) добавления новой вершины u и ребер (v, u), (u, w).

Определение. Дополнением графа G = (V, X) называют граф`G = (V,`X), где`X — множество всех возможных ребер между V, отсутствующих в G .

Пример 1. В графе G = (V, X) (V = (1, 2 , 3), X = ((1, 2), (2, 3))) из примера 4 п. 1.1 дополнение G₁= (V₁, X₁) =(V₁= (1, 2 ,3), Х₁ = (1, 3)) и результат подразбиения ребра (1, 2)(граф G₂ = (V₂, X₂) = (V₂= (1, 2, 3, 4), Х₂ = ((1 ,4), (4, 2), (2, 3))) графически можно представить в следующем виде:

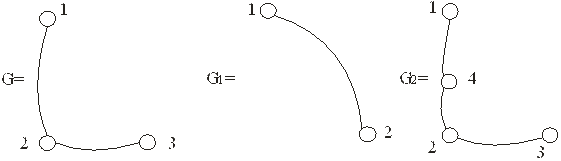
Рис.2.1

Для характеристики структурных и комбинаторных свойств графов также используется понятие изоморфизма. Данное понятие является универсальным в математике. Если заданы множества А и В с введенными на них операциями f₁ и f₂, то изоморфизмом называют взаимно однозначное отображение x множеств А в В и f₁(А) в f₂(В), сохраняющее операции f₁ и f₂. При этом для "аÎА из b=x(a) следует: f₂(b)=x(f₁(a)). В частном случае для графов определение принимает следующий вид.

Определение. Графы (псевдографы) G=(V,X) и H= (W, Y) изоморфны, если существуют взаимно однозначные отображения j : V® W, y : X ®Y, такие, что для каждого ребра x = (v,u) Î X cправедливо: y(x) = (j(v), j(u)).

Можно в качестве исходных множеств у графов принять вершины, а операцией — соединение их ребрами, можно и наоборот — исходными считать множества ребер, а операцией — соединение их вершинами. Отображение x построено из двух частей — jи y. Из взаимно однозначного характера отображений jи yвытекают простейшие необходимые условия существования изоморфного отображения графов G₁ = (V₁ , X₁) и G₂ = (V₂ , X₂) . G₁и G₂должны иметь одинаковые:

1) числа вершин(½V₁½=½V₂½);

2) числа рёбер(½Х₁½=½Х₂½).

Изоморфные графы имеют одинаковую структуру в смысле наличия соединений между внутренними элементами. Граф G₁, изоморфный некоторому исходному графу G, отличается от него лишь обозначением вершин.

Пример 2. Рассмотрим графы G = (V, X) (V = (1, 2, 3), X = ((1, 2), (2, 3)) и Н = (W,Y) = (W = (5, 6 , 8), Y = ((5, 8),(6,8)). Они изоморфны, так как искомые взаимно однозначные отображения j: V® W иy: X ®Y существуют. На рис.2.2 они показаны графически. В виде списков отображения jи y можно представить следующим образом:

j : {1«5; 2«8; 3 «6}; y : {(1,2) «(5,8); (2,3)«(6,8)}.

Рис.2.2

Второй возможный вариант отображений j и y имеет вид:

j : {1 «6; 2«8; 3«5};

y : {(1,2) «(6,8); (2,3)«(5,8)}.

При изоморфных отображениях соответствующие ребра соединяют соответствующие вершины. Как видно из примера 2, задание изоморфных отображений (в том случае, если они существуют) может быть выполнено неединственным способом.

Определение. Автоморфизмом является изоморфное отображе-ние графа на себя.

Пример 3. Для графа G = (V, X) из Примера 2 автоморфизм задаётся отображениями

j : {1 «3; 2«2}; y : {(1,2) «(3,2); (2,3)«(2,1)}.

Практически проверка изоморфизма графов осуществляется с использованием их матричных представлений. Для матриц смежности и инцидентности справедливы следующие очевидные утверждения.

Теорема 2.1.Графы (орграфы) изоморфны тогда и только тогда, когда их матрицы смежности могут быть получены одна из другой одновременной перестановкой одинаковых пар строк и столбцов.

Теорема 2.2.Графы (орграфы) изоморфны тогда и только тогда, когда их матрицы инцидентности могут быть получены одна из другой путем произвольных перестановок строк и столбцов.

Пример 4. Рассмотрим графы G = (V, X), V = (1, 2, 3, 4), X = ((1, 2), (1, 3), (2, 3), (2,4), (3, 4)) и Н = (W,Y), W = (5, 6, 7, 8), Y = ((5, 6), (5, 8), (6,7), (6, 8), (7, 8)) (рис.2.3) .

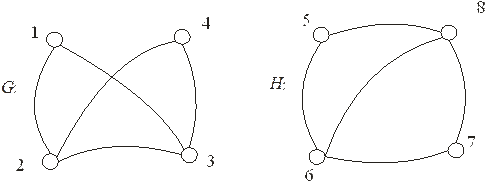
Рис.2.3

Располагая вершины в порядке возрастания их номеров, получим матрицы смежности графов следующего вида:

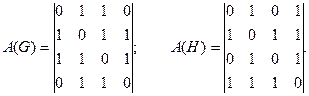
Матрица А(Н) может быть получена из матрицы A(G)путем одновременной перестановки строк 3 и 4 и столбцов 3 и 4. Следовательно, Графы G и Н изоморфны и с учетом нумерации вершин в графах искомое отображение вершин имеет вид:

j : {1 «5; 2«6; 3«8; 4«7}.

Располагая ребра в графах в лексикографическом порядке, получим матрицы инцидентности графов следующего вида:

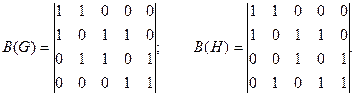
Матрица В(Н) может быть получена из матрицы В(G)путем перестановки строк 3 и 4 и столбцов 3 и 4.

Определение. Граф Н является подразбиением графа G, если он может быть получен из G последовательным применением операции подразбиения рёбер. Графы G и Н гомеоморфны, если у них существуют изоморфные подразбиения.

Очевидно, для проверки гомеоморфности графов, достаточно устранить у них все подразбиения ребер и проверить изоморфизм полученных графов.

Задачи

1. Найти дополнения графов: K _n , K_n,m .

2.Выяснить изоморфизм следующих пар графов. При положительном ответе построить примеры взаимно однозначных отображений на множествах вершин и рёбер. Отрицательный ответ обосновать.

а) G = (V, X), (V = (1,3 ,5,7), X = ((1,3), (3,5), (1, 7)));

Н = (W, Y),(W = (2,4 ,8), Y= ((2,8), (2,4), (4, 8)));

б) G = (V, X), (V = (1,3 ,6), X = ((1,3), (3,6), (1, 6)));

Н = (W, Y),(W = (2,4 ,7), Y= ((2,7), (4, 7)));

в) G = (V, X), (V = (1,3 ,6), X = ((1,3), (3,6), (1, 6)));

Н = (W, Y),(W = (2,5 ,7), Y= ((2,7), (2,5), (5, 7)));

г) G = (V, X), (V = (1,2 ,5,8), X = ((1,2), (2,5), (1,5)));

Н = (W, Y),(W = (3,4 ,6, 9), Y= ((3,9), (4,9), (6,9))).

3. Перечислить все возможные неизоморфные графы с тремя вершинами.

4. Перечислить все возможные неизоморфные деревья с четырьмя вершинами.