Метод сигнальных графов
В основе анализа электрических цепей, изложенного ранее, лежат законы Кирхгофа. Возможен, однако, под- i ход, основанный на причинно-следственных связях между токами и напряжениями в- различных участках схемы, названный методом сигнальных графов.
В отличие от графов рассмотренных ранее, в направленных графах прохождения сигналов (рис. 17 а) каждый узел (вершина) отображает какую-нибудь переменную, а каждая ветвь, соединяющая эти узлы отображает причинно-следственную связь между ними: стрелка на ветви показывает направление передачи: от причины к следствию, а символ соответствующий стрелке, является оператором величины передачи ветви, равной отношению выходной переменной к входной рис.17 б.
Таким образом, одиночная ветвь, связывающая узлы сигнального графа, отображает графически взаимосвязь между переменными, а совокупность узлов и ветвей в виде сигнального графа является топологической моделью системы линейных уравнений и позволяет наглядно представить взаимосвязи различных переменных и коэффициентов этих уравнений. В теории электрических цепей узлами графа обычно являются токи и напряжения- сигналы , отсюда название графа - сигнальный, а ветвями - проводимости, сопротивления или безразмерные величины коэффициентов передач;.
Простейшему уравнению 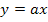 соответствует граф на рис.17 б, имеющий два узла (переменные ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
соответствует граф на рис.17 б, имеющий два узла (переменные ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 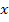 и ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
и ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 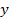 ) и одну ветвь ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
) и одну ветвь ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 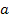 , направленную от причины ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
, направленную от причины ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 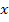 к следствию ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
к следствию ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 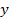 . Узел, отображающий на графе независимую (входную) переменную, называется истоком, а отображающий выходную (зависимую) переменную -стоком. Исток должен содержать только исходящие ветви, а сток -входящие. Прочие узлы называют смешанными. Сигнал передается от одного узла к другому только в направлении стрелки. Поэтому переменная в узле определяется только входящими ветвями, выходящие из узла ветви не оказывают на нее никакого влияния.
. Узел, отображающий на графе независимую (входную) переменную, называется истоком, а отображающий выходную (зависимую) переменную -стоком. Исток должен содержать только исходящие ветви, а сток -входящие. Прочие узлы называют смешанными. Сигнал передается от одного узла к другому только в направлении стрелки. Поэтому переменная в узле определяется только входящими ветвями, выходящие из узла ветви не оказывают на нее никакого влияния.
Теория графов позволяет по определенным правилам провести упрощение сложного графа к более простому виду, из которого можно легко определить передачу графа. Такая процедура эквивалентна алгебраическому решению системы уравнений. Основные правила эквивалентных преобразований поясняющие их примеры приводятся далее,
1. Передача нескольких параллельных, одинаково направленных ветвей равна сумме передач этих ветвей (рис.18а).
2. Передача нескольких последовательных ветвей, соединяющих простые узлы (см. далее), образует путь сигнала, равный произведению передач, входящих в эту последовательность ветвей (рис.18 б). Простым называет узел графа, к которому не подсоединена петля или контур,
3. Исключение петли. Петлей называется ветвь, начинающаяся и кончающаяся в данном узле. Простейшему графу, содержащему петлю (рис.18 в), соответствует уравнение
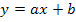 или
или 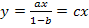
Отсюда очевидно, что исключение петли меняет коэффициент передачи ветвей, которые заканчивались в узле, содержащем петлю 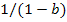 .
.
4. Устранение контура. Контур междукакими-либо узлами имеется направлениями ветвей (рис.18 г).
образуется в графе, когда два пути с противоположными Для передачи от 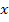 к
к 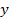 :
:
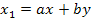
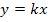
Откуда
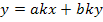
Первый член отображается ветвью с передачей 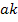 , а второй -петлей с передачей
, а второй -петлей с передачей 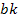 . Для передачи от
. Для передачи от 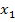 к
к 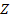 контур
контур 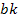 представляет петлю в
представляет петлю в 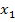 и его устранение равноценно устранению петли по правилу 3.
и его устранение равноценно устранению петли по правилу 3.
5. Контурная передача 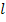 находится после разрыва любой из ветвей контура в любом ее месте. Отношение сигнала, пришедшего к разрыву после обхода контура, к сигналу, посланному в разрыв, называется контурной передачей. Разрывать выбранную ветвь на части надо так, чтобы по одну сторону оставалась ветвь с исходным значением передачи, а по другую - ветвь с единичной передачей, не изменяющая величины передачи вдоль контура. Для рис.18 д, пользуясь правилами 2 и 3, находим значение контурной передачи
находится после разрыва любой из ветвей контура в любом ее месте. Отношение сигнала, пришедшего к разрыву после обхода контура, к сигналу, посланному в разрыв, называется контурной передачей. Разрывать выбранную ветвь на части надо так, чтобы по одну сторону оставалась ветвь с исходным значением передачи, а по другую - ветвь с единичной передачей, не изменяющая величины передачи вдоль контура. Для рис.18 д, пользуясь правилами 2 и 3, находим значение контурной передачи
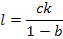
6. Инверсия пути представляет изменение направления какого-либо пути графа на обратное, т.е. замену причины и следствием, что эквивалентно решению уравнений относительно новой переменной. Для графа, приведенного на рис.18 е, уравнение имеет вид
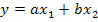
после инверсии
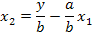
В инвертированном графе ветвь от 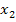 к
к 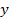 изменяет направление на обратное. Таким образом, при инверсии необходимо изменить направление стрелок всех ветвей, входящих в инвертируемый путь; изменить на обратные (
изменяет направление на обратное. Таким образом, при инверсии необходимо изменить направление стрелок всех ветвей, входящих в инвертируемый путь; изменить на обратные ( 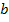 на
на 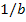 и т.д.) передачи всех ветвей, входящих в инвертируемый путь; концы не инвертируемых ветвей, подходившие к концам ветвей, подлежащих инверсии, после ее выполнения должны находиться там, где теперь находятся концы инвертированных ветвей. Передачи каждой из этих неинвертируемых ветвей делятся на передачу инвертируемой ветви с обратным знаком.
и т.д.) передачи всех ветвей, входящих в инвертируемый путь; концы не инвертируемых ветвей, подходившие к концам ветвей, подлежащих инверсии, после ее выполнения должны находиться там, где теперь находятся концы инвертированных ветвей. Передачи каждой из этих неинвертируемых ветвей делятся на передачу инвертируемой ветви с обратным знаком.
7. Общая формула передачи графа (формула Мэзона) имеет вид
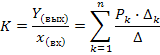
где Рк - передача К -го прямого пути, т.е. пути в котором узлы не встречаются более одного раза от 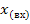 до
до 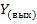
n – число путей; 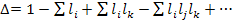 ;
;
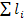 – сумма передач всех контуров и петель ;
– сумма передач всех контуров и петель ;
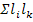 - сумма перемноженных попарно передач всех контуров и петель, не касающихся друг друга, т.е. не имеющих общих узлов;
- сумма перемноженных попарно передач всех контуров и петель, не касающихся друг друга, т.е. не имеющих общих узлов;
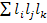 - сумма перемноженных по трое передач всех контуров и петель не касающихся друг друга;
- сумма перемноженных по трое передач всех контуров и петель не касающихся друг друга;
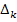 - имеет тот же смысл, что и
- имеет тот же смысл, что и  , только относится к передачам контуров и петель, не касающихся К-го пути.
, только относится к передачам контуров и петель, не касающихся К-го пути.
Например, в графе на рис.19 передача от x к y складывается из двух прямых путей

Четырех контырных передач
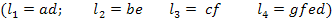
И одной плети
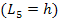
Путь P2 не соприкасается только с 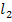 , поэтому
, поэтому 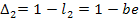 . Для назодления
. Для назодления  из графа отыскиваем
из графа отыскиваем 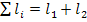 +
+ 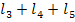 , попарно не касаются дргу друга, в данном графе нет. В результате по формуле Мэзона находим полную передачу графа
, попарно не касаются дргу друга, в данном графе нет. В результате по формуле Мэзона находим полную передачу графа
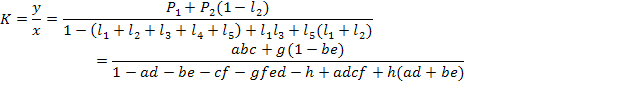
Наибольшее распространение (особенно при анализе электронных схем) получил метод узловых напряжений, приводящий к
значительному сокращению числа уравнений для схем, содержащих общий базовый узел.
Для получения сигнального графа в форме напряжения (или ток) на входе устройства (причина) - напряжение (или ток) на выходе устройства (следствие) обратимся к уравнению . Представим правую часть этого уравнения некоторые эквивалентным током 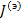 , т.е.
, т.е.
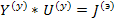
где 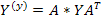 - матрица узловых проводимостей. Рассмотрим структуру матрицы узловых проводимостей. Если обозначить через
- матрица узловых проводимостей. Рассмотрим структуру матрицы узловых проводимостей. Если обозначить через 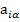 элементы матрицы инциденций
элементы матрицы инциденций 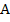 , то элемент транспортированной матрицы
, то элемент транспортированной матрицы 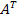 есть
есть 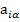 . Элементы матрицы проводимости ветвей
. Элементы матрицы проводимости ветвей 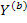 обозначим
обозначим 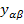 . Поскольку
. Поскольку 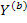 - диагональная матрица, то
- диагональная матрица, то

Тогда отдельный элемент матрицы узловых проводимостей согласно правилам произведения матриц выражается так
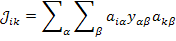
Представим матрицу 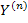 как сумму 2 матриц
как сумму 2 матриц
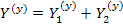
Здесь 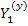 - диагональная матрица с элементами
- диагональная матрица с элементами
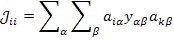
при 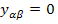 для
для 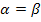 ,
,
Преобразуем матрицу
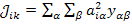 ,
,
откуда следует, что эти элементы не отрицательны, так как 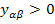 . В то же время
. В то же время 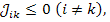 поскольку
поскольку 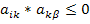 , так как сомножители всегда имеют разные знаки.
, так как сомножители всегда имеют разные знаки.
Используя уравнение, запишем матричное уравнение в виде
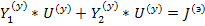
и умножим каждый член его слева на 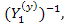 затем выразим узловое напряжение
затем выразим узловое напряжение
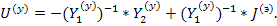
Элементы обратной матрицы 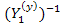 , поскольку она диагональная, равна
, поскольку она диагональная, равна 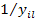 . Тогда, если ввести матрицу
. Тогда, если ввести матрицу 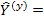
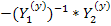 с элементами
с элементами 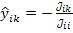 , то уравнение в развернутой форме примет вид:
, то уравнение в развернутой форме примет вид:
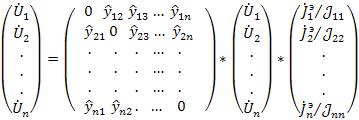
Сигнальный граф, построенный в соответствии с системой уравнений, описываемых матричным уравнением, имеет структуру, показанную на рис.20 б. Передачи ветвей графа могут быть найдены алгебраически по матрицам 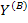 , А. Однако для практической (не машинной) реализации более удобна предлагаемая далее процедура.
, А. Однако для практической (не машинной) реализации более удобна предлагаемая далее процедура.
Для получения сигнального графа по схеме электрических цепей выбирают базовый узел и вводят узловые потенциалы; источники напряжения, содержащиеся в ветвях (кроме входной) преобразуют в источники тока и определяют 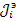 ; пересчитывают все сопротивления в проводимости (в общем случае комплексные или преобразованные по Лапласу); находят проводимости ветвей
; пересчитывают все сопротивления в проводимости (в общем случае комплексные или преобразованные по Лапласу); находят проводимости ветвей 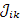 и узловые проводимости
и узловые проводимости 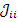 ; определяют передачи ветвей
; определяют передачи ветвей 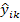 . Узловые проводимости
. Узловые проводимости 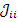 представляют собой проводимость данного узла относительно базового, найденную из условия короткого замыкания всех остальных узлов (т.е. их замыкания на базовый узел). Это условие приводит к следующей формуле для определения собственной узловой проводимости:
представляют собой проводимость данного узла относительно базового, найденную из условия короткого замыкания всех остальных узлов (т.е. их замыкания на базовый узел). Это условие приводит к следующей формуле для определения собственной узловой проводимости:
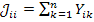 ,
,
где 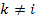 и берутся только те проводимости, которые связывают
и берутся только те проводимости, которые связывают 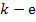 узлы с данным
узлы с данным
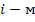 узлом. Взаимные проводимости узлов
узлом. Взаимные проводимости узлов 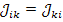 представляют собой фактически проводимости ветвей, соединяющих узлы
представляют собой фактически проводимости ветвей, соединяющих узлы 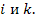 Таким образом,
Таким образом, 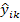 представляет собой взятую с обратным знаком проводимость ветви, соединяющей узел
представляет собой взятую с обратным знаком проводимость ветви, соединяющей узел 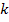 с узлом
с узлом 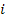 , деленную на собственную проводимость узла
, деленную на собственную проводимость узла 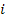 . Учитывая это и формулы
. Учитывая это и формулы
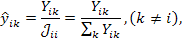
где узловая проводимость 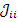 имеет физический смысл весового коэффициента для передачи к данному узлу
имеет физический смысл весового коэффициента для передачи к данному узлу 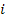 . Аналогично противоположная передача от
. Аналогично противоположная передача от 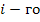 узла к
узла к 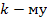 равна
равна
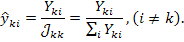
В цепях, не содержащих невзаимных элементов, 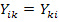 .
.
Далее выбирают на плоскости узлы (кроме базового) с узловыми переменными
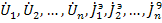 .
.
и соединяют их ветвями с передачей 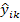 для пар узлов
для пар узлов 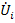 и
и 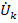 ,
, 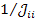 для передачи от узлов
для передачи от узлов 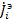 и
и 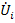 и
и 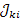 для передач от узлов
для передач от узлов 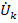 к
к 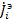 , что приводит к графу, называемому нормализованным сигнальным графом проводимостей. На рис.20 показан пример построения сигнального графа по описанной процедуре. На схеме цепи (рис.20 а) в качестве базового узла взят узел 0. Напряжения узлов 1,2,3,4 относительно узла 0 равны
, что приводит к графу, называемому нормализованным сигнальным графом проводимостей. На рис.20 показан пример построения сигнального графа по описанной процедуре. На схеме цепи (рис.20 а) в качестве базового узла взят узел 0. Напряжения узлов 1,2,3,4 относительно узла 0 равны 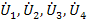 и на ряду с узлом
и на ряду с узлом 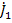 составляют переменные графа (рис.20 б). Собственная узловая проводимость
составляют переменные графа (рис.20 б). Собственная узловая проводимость 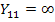 , так как внутреннее сопротивление источника
, так как внутреннее сопротивление источника 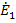 равно 0 и эта передача от узла 2 к узлу 1
равно 0 и эта передача от узла 2 к узлу 1 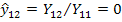 обозначена пунктиром на рис.20 б. Собственная проводимость узла 2 равна
обозначена пунктиром на рис.20 б. Собственная проводимость узла 2 равна 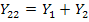 . Способ определения собственных проводимостей проиллюстрирован на примере узла 3 (рис.20 в): закорачивая узлы 2 и 4, получаем
. Способ определения собственных проводимостей проиллюстрирован на примере узла 3 (рис.20 в): закорачивая узлы 2 и 4, получаем 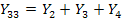 . Аналогично
. Аналогично 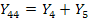 . Взаимные проводимости:
. Взаимные проводимости:
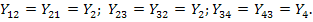
Узел источника тока 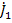 соединяется с узлами
соединяется с узлами 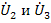 через передачи
через передачи 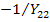 и
и 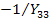 . Деля взаимные передачи, входящие в узлы, на собственные проводимости узлов приходим к структуре графа, показанной на рис.20 б.
. Деля взаимные передачи, входящие в узлы, на собственные проводимости узлов приходим к структуре графа, показанной на рис.20 б.
Необходимо обратить внимание на то, что источник тока отображается на графе ветвями с взаимными передачами 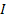 и
и 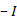 (рис. 20 г), после деления которых на проводимости узлов получаем структуру на рис.20 д, использованную в графе на рис.20 б.
(рис. 20 г), после деления которых на проводимости узлов получаем структуру на рис.20 д, использованную в графе на рис.20 б.
При наличии нескольких ветвей от источника тока в уравнение в качестве 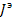 войдет их сумма для тех узлов, с которыми связаны данные источники тока. Если источник тока является входным для некоторого устройства так, что один из его плюсов заземлен (рис. 21 а), то входная часть графа отобразиться одной ветвью с передачей
войдет их сумма для тех узлов, с которыми связаны данные источники тока. Если источник тока является входным для некоторого устройства так, что один из его плюсов заземлен (рис. 21 а), то входная часть графа отобразиться одной ветвью с передачей 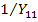 (рис.21 б).
(рис.21 б).
Дата добавления: 2015-10-13; просмотров: 2324;
