Тензорный метод

Тензорный метод анализа для расчета сложных систем (электрических, механических и др.) был разработан Г.Кроном, который назвал его диакоптикой.

Термин «диакоптика» происходит от греческого слова «копто», озночающего «разрывать» или «разделять на части» и приставки «диа», которая усиливает значение следующего за ней слова. Согласно диакоптике, т.е. методу исследования сложных систем по частям, реальные физические системы можно разделить на части (элементарные или примитивные цепи), рассчитываемые по отдельности, как если бы остальные части системы не существовали. Затем частные решения соединяются шаг за шагом до тех пор, пока не будет получено решение для всей системы.

Рассмотрим некоторую цепь общего вида, в которой действуют источники

напряжения и тока, а между отдельными ветвями существует магнитная связь (взаимоиндукция).

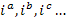Пусть в ветвях схемы цепи протекают неизвестные токи . Выбираем в качестве вспомогательных неизвестных токи хорд (ветвей связи графа данной цепи). Обозначим эти токи, которые могут трактоваться как контурные, через … .

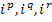Контурные точки можно рассматривать как координаты вектора 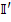в -мерном пространстве (или, проще, пространстве .

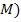Токи ветвей можно рассматривать как координаты некоторого другого вектора 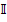и 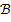-мерном пространстве (или, проще, пространстве 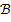). Введенные векторы токов выражаются матрицами

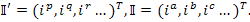
Расположение индексов вверху означает, что эти векторы контрварианты. Токи ветвей всегда можно выразить с помощью I-го закона Кирхгофа или, что одно и то же, приравнять их сумме контурных токов, протекающих в ветвях.

В результате получается следующее выражение:

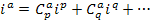
Каждый коэффициент 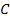равен 0, +1 или -1 в зависимости от наличия тока в рассматриваемой ветви и от совпадения его направления с принятым для данной ветви за положительное.

Таблица коэффициентов 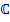может рассматриваться как матрица преобразования от 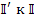, т.е.

Введенная матрица 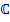, называемая также матрицей связи или соединений, при соответсвующем выборе дерева графа цепи совпадает с ранее рассмотренной транспортированной матрицей главных контуров, т.е.

.

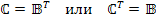Для произвольной обобщенной ветви на рис.16 в соответствии с принятыми обозначениями для ветви 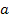уравнение можно записать в виде

Матрицы, составленные из напряжений и э.д.с. ветвей

,

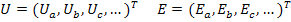представляют собой ковариантные векторы (отмечены нижними индексами). Расходуемая в цепи мощность

,

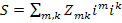откуда следует, что матрица

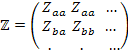
представляет собой дважды ковариантный тензор (тензор полных сопротивлений). Диагональные члены 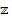представляют собой собственные полные сопротивления ветвей, а внедиагональные определяются электромагнитной связью ветвей.

В обратимых цепях 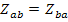. Например, при взаимоиндукции с коэффициентом 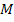двух ветвях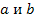

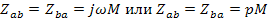
(при решении конкретных задач необходимо придерживаться правил знаков для согласного и встречного включений).

Обобщая соотношение для всех ветвей, запишем

ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">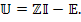

Рассмотрим преобразование, позволяющее перейти от пространства 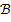к пространству 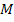. Оно определенно матрицей связи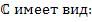

Индексные обозначения	Матричные обозначения
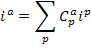
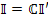
		- определение матрицы связи
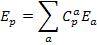
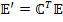
		- ковариантный вектор
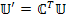
		- ковариантный вектор
		- дважды ковариантный тензор

Здесь 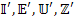- матрицы, представляющие соответствующие тензорные величины в пространстве .

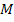Соотношение, связывающее тензорные величины, не зависит от выбора системы координат и в пространстве 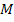приобретает вид

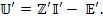
Элементы матрицы 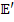представляют собой алгебраическую сумму э.д.с., действующих в контурах. Элементы главной диагонали 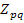представляют собой собственные сопротивления контуров, а остальные элементы этой матрицы являются сопротивлениями связи между контурами. Каждый элемент матрицы 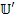- это сумма разностей потенциалов между зажимами элементов ветвей, встречаемых при последовательном обходе контура. Из 2-го закона Кирхгофа эта сумма равна нулю.

Отсюда

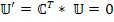
(в ранее приведенных обозначениях это соответствует 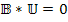). Таким образом, соотношение значительно упрощается в пространстве 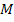и становиться системой из 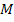уравнений с 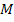искомыми неизвестными:

.

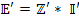В основе эквивалентных преобразований электрических цепей в диакоптике лежит постулат инвариантности мощности

.

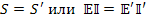Последовательность решения задачи методом диакоптики для чистоконтурной цепи (рис.22 а), т.е. цепи, содержащей число контуров равное числу элементарных двухполюсных ветвей, такова.

1. Устанавливают примитивную контурную цепь. Например разделив исходную цепь на 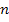короткозамкнутых частей с токами короткого замыкания, равными токам исходной ветви и приложенными э.д.с. (рис.22 б).

2. Устанавливают тензор полного сопротивления 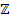примитивной цепи с числом строк и столбцов, равных числу элементов примитивной цепи.

3. Записывают вектора r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 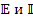примитивной цепи.

4. Получают матрицу преобразований .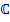

5. Определяют новые компоненты тензора полного сопротивления

6. Записывают контурные напряжения 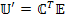и уравнение напряжения новой цепи .

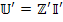7. Производят обращение тензора полного сопротивления новой цепи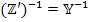

8. Находят неизвестные токи и напряжения .

Разумеется для простых цепей применение диакоптики не оправдано, однако, по мере усложнения цепи и наличия в ней отдельных идентичных элементарных цепей при большом числе электромагнитных связей, затраты умственного и физического труда с применением диакоптики сокращаются пропорционально сложности цепи. Кроме того, применение диакоптики позволяет активно использовать машинные методы расчета.