Теория четырехполюсников
Под четырехполюсниками понимают электрическую цепь или часть цепи (рис.23) с двумя парами зажимов. Пусть входными переменными являются  , а выходными
, а выходными 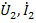 . Любые две из указанных величин можно считать зависимыми и выразить в виде уравнений четырехполюсника через две остальные, принятые за независимые. Число таких уравнений равно шести – числу сочетаний из четырех по два. Коэффициенты уравнений четырехполюсника называют параметрами четырехполюсника.
. Любые две из указанных величин можно считать зависимыми и выразить в виде уравнений четырехполюсника через две остальные, принятые за независимые. Число таких уравнений равно шести – числу сочетаний из четырех по два. Коэффициенты уравнений четырехполюсника называют параметрами четырехполюсника.
При представлении через параметры проводимостей входное и выходное напряжения ( 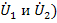 считают аргументами, а токи (
считают аргументами, а токи (  функциями этих аргументов. Взаимосвязь между выбранными переменными можно изобразить в виде сигнального графа (рис.24 а), на котором независимые узлы-источники отмечены условно черными, а зависимые стоки-белыми полукругами. Передачами ветвей служат проводимости. Матричное уравнение, связывающее переменные в соответствии с графом, имеет вид
функциями этих аргументов. Взаимосвязь между выбранными переменными можно изобразить в виде сигнального графа (рис.24 а), на котором независимые узлы-источники отмечены условно черными, а зависимые стоки-белыми полукругами. Передачами ветвей служат проводимости. Матричное уравнение, связывающее переменные в соответствии с графом, имеет вид
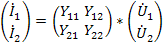
Физический смысл параметров проводимости четырехполюсника определяется из опытов короткого замыкания, а именно: входные проводимости слева и справа при короткозамкнутых противоположных выводах
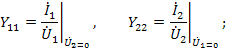
а передаточные проводимости
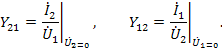
В цепях, соответствующих принципу обратимости, 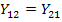 , и, если
, и, если 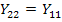 , то четырехполюсник не различим со стороны входных и выходных зажимов и называется симметричным.
, то четырехполюсник не различим со стороны входных и выходных зажимов и называется симметричным.
Если в качестве независимых переменных выбрать токи ( 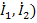 , а зависимых-напряжения (
, а зависимых-напряжения ( 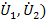 , то взаимосвязь между переменными устанавливается через параметры сопротивлений в виде графа, показанного на рис.24 б и матричного уравнения
, то взаимосвязь между переменными устанавливается через параметры сопротивлений в виде графа, показанного на рис.24 б и матричного уравнения
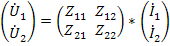
Физический смысл коэффициентов четырехполюсника в данном случае выражается при холостом ходе, а именно: входные сопротивления четырехполюсника слева и справа при разомкнутых противоположных выводах
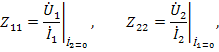
и передаточные сопротивления

В обратимых цепях  и, если
и, если 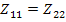 , то четырехполюсник симметричный. Из сравнения формул видно, что матрица параметров сопротивлений (
, то четырехполюсник симметричный. Из сравнения формул видно, что матрица параметров сопротивлений ( 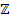 ) является дуальной матрице параметров проводимостей (
) является дуальной матрице параметров проводимостей ( 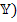 , причем (
, причем ( 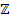 )* (
)* ( 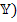 =1.
=1.
Выразим напряжение и ток на входе через напряжение и ток на выходе. Из уравнений получаем:

Здесь 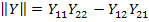 - есть детерминант матрицы проводимостей
- есть детерминант матрицы проводимостей 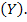
Физический смысл введенных параметров  можно установить из рассмотрения режимов холостого хода на выходе
можно установить из рассмотрения режимов холостого хода на выходе
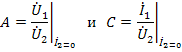
и короткого замыкания на выходе
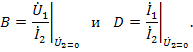
Для линейного пассивного четырехполюсника определитель
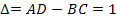 ,
,
а для симметричного 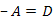 .
.
Сигнальный граф четырехполюсника в форме 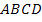 показан на рис. 24 в. Изменяя знаки токов на противоположные (рис.23 б) и решая систему относительно выходных величин, получаем
показан на рис. 24 в. Изменяя знаки токов на противоположные (рис.23 б) и решая систему относительно выходных величин, получаем

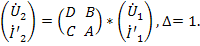
Этой системе соответствует граф, показанный на рис.24 г.
Оставшиеся две системы уравнений выражают через смешанные (гибридные) переменные по размерности и индексу:
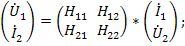
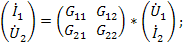
В данных уравнениях выполняются соотношения:

а также
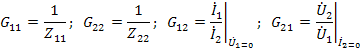
Для обратимых цепей в t wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>21</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  ; в симметричных четырехполюсниках
; в симметричных четырехполюсниках 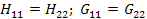 .
.
Каждая система параметров может оказаться более удобной при определенном типе задач. Все рассмотренные параметры связаны друг с другом и могут быть выражены одни через другие.
Для определения параметров четырехполюсников проводят два опыта: холостого хода при
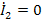 (выходные зажимы разомкнуты) и короткого замыкания при
(выходные зажимы разомкнуты) и короткого замыкания при
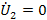 (выходные зажимы закорочены). В опыте холостого хода
(выходные зажимы закорочены). В опыте холостого хода
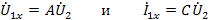 ,
,
откуда 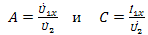
и входное сопротивление со стороны первичных зажимов
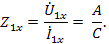
В опыте короткого замыкания
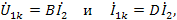
откуда
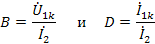
и входное сопротивление со стороны первичных зажимов 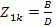
Аналогичные опыты при питании со стороны вторичных зажимов приводят к формулам:
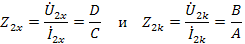
Совместное решение уравнений дает
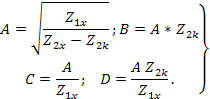
Сопоставляя сигнальные графы, представляющие рассмотренные системы, между собой, можно отметить, что независимые переменные в каждом графе образуют вершине – истоки, а зависимые – стоки.
Соединение четырехполюсников можно отобразить соединением их графов, которое осуществляется либо наложением, либо составлением вершин двух смежных графов. Если некоторая переменная цепи является независимой одновременно для нескольких обьеденяемых четырехполюсников, то вершины – источники отдельных графов должны быть обьеденены (наложены ) в одну общую вершину-источник полного графа. Напротив, если первичная переменная одного четырехполюсника оказывается зависимой для другого, то при соединении их графов вершина – источник и вершина – сток образуют (составлением) внутреннюю вершину, соответствующую этой переменной.
Таким образом, правило соединения графов гласит: «Все налагаемые друг на друга вершины должны быть одного типа, а составленные – различных типов.»
Принципы возможного соединения четырехполюсников и соответствующие им графы показаны на рис. 25. Структуры результирующих графов получаются из соединения соответствующих графов рис. 24 и проилюстрированны на примере параллельного соединения (рис. 25 а): входные и выходные переменные 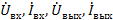 связаны между собой через ветви с единичной передачей и графов четырехполюсников I и II. Из анализа полного графа видно, что он описывается матричным уравнением.
связаны между собой через ветви с единичной передачей и графов четырехполюсников I и II. Из анализа полного графа видно, что он описывается матричным уравнением.
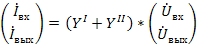
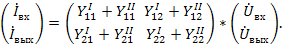
Аналогично суммированием соответствующих матриц находиться результирующие параметры для последовательно-паралельного соединения (рис 25. б) и параллельно-последовательного соединения (рис.25 в). Для каскадного соединения (рис.25 д) результирующая матрица, как это следует из графа, находиться произведением матриц
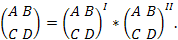
Приведенные правила могут быть распространены на случаи соединения большого числа четырехполюсников. Все указанные виды соединений широко используются в цепях электроники и электроавтоматики, а в последнее время на функциональном уровне проектирования систем.
Введем характеристические параметры четырехполюсника: характеристическое сопротивление и характеристический коэффициент передачи, которые широко используются в теории электрических фильтров.
Характеристическим (повторным) сопротивлением симметричного четырехполюсника называют такое сопротивление  , которое, будучи присоединенным к выходным (входным) зажимам, приводит к тому, что его входное (выходное) сопротивление также будет равно
, которое, будучи присоединенным к выходным (входным) зажимам, приводит к тому, что его входное (выходное) сопротивление также будет равно  . Для несимметричного четырехполюсника существует два характеристических сопротивления
. Для несимметричного четырехполюсника существует два характеристических сопротивления 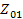 и
и 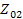 , такие, что при включении
, такие, что при включении 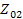 к зажимам 2, 2’ (рис 26. а) характеристическое сопротивление со стороны зажимов 1, 1’ равно
к зажимам 2, 2’ (рис 26. а) характеристическое сопротивление со стороны зажимов 1, 1’ равно 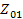 и наоборот, при включении к зажимам 1, 1’ (рис.26 б) сопротивления
и наоборот, при включении к зажимам 1, 1’ (рис.26 б) сопротивления 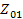 , сопротивление на зажимах 2, 2’ равно
, сопротивление на зажимах 2, 2’ равно 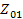 .
.
По определению:
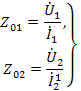
Рассмотрим сигнальный граф прямой и обратной передач четырехполюсника, когда он нагружен на соответствующее характеристическое сопротивление (рис.26 в,г). Для определения 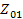 из графа на рис.26 в по формуле и необходимо найти передачу от
из графа на рис.26 в по формуле и необходимо найти передачу от 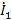 к
к 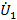 , при етом узел
, при етом узел 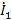 , должен быть истоком, а ветвь
, должен быть истоком, а ветвь 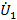 – стоком. Узел
– стоком. Узел 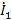 можно превратить в исток, инвертируя ветвь D, т.е. направив ее в
можно превратить в исток, инвертируя ветвь D, т.е. направив ее в 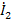 . После инверсии ее передача станет равной 1/D, кроме того, ветвь С, входящая в этот узел, теперь должна быть направлена также в узел
. После инверсии ее передача станет равной 1/D, кроме того, ветвь С, входящая в этот узел, теперь должна быть направлена также в узел 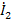 , а ее передача будет равно –C/D (рис.26 д)
, а ее передача будет равно –C/D (рис.26 д)
По формуле Мэзона из графа, показанного на рис.26 д, получим
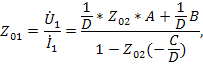
откуда 
Аналогично, преобразуя граф обратной передачи (рис.26 г), получаем граф, показанный на рис. 26 е, из которого
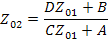
Решая систему из двух последних уравнений, получаем
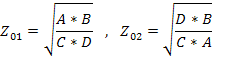
Используя взаимосвязь параметров четырехполюсника, можно выразить характеристические сопротивления через параметры холостого хода и короткого замыкания, откуда
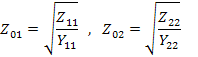
Для симметричного четырехполюсника 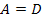 ,
,  так, что
так, что
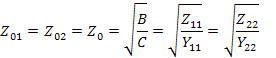
Из уравнений найдем
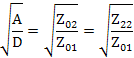
Характеристические сопротивления не описывают полностью поведение четырехполюсника, так как каждое из них относиться лишь к одной паре зажимов. Вторым основным характеристическим параметром является характеристическая передача. Вычислим коэффициенты передач четырехполюсника по току и напряжению. Из графа на рис. 26 находим 
Для получения передачи по напряжению узел 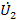 надо превратить в источник, инвертируя ветвь
надо превратить в источник, инвертируя ветвь 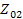 (рис.26 ж). Из полученного графа находим
(рис.26 ж). Из полученного графа находим

Подставляя в выражения получаем
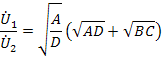

Полученные выражения содержат общий множитель, имеющий определенный физический смысл. Для симметричного четырехполюсника ( 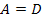 ) при согласованной нагрузке (
) при согласованной нагрузке ( 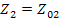 )
)

Рассматривая обратную передачу и, учитывая, что AD-BC=1, найдем
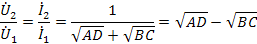
Передача четырехполюсника, таким образом, выражается некоторым комплексным числом, которое можно записать в показательной форме


Здесь 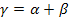 – характеристический коэффициент передачи или постоянная распространения;
– характеристический коэффициент передачи или постоянная распространения; 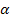 – коэффициент затухания (в неперах – I п =8,686 Дб);
– коэффициент затухания (в неперах – I п =8,686 Дб);
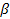 – коэффициент фазы(рад).
– коэффициент фазы(рад).
Таким образом, отношение напряжений или токов равно комплексному числу, модуль которого показывает во сколько раз уменьшилась амплитуда сигнала на выходе четырехполюсника, а аргумент- как при этом изменилась его фаза. Используя уравнения , получим коэффициенты передачи четырехполюсника по напряжению и току в следующем виде:
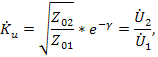
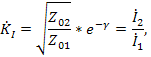
Подставляя выражения в формулы для гиперболических функций, можно найти ряд полезных соотношений , используемых в теории фильтров:
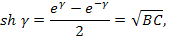
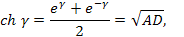

Дополнив последние уравнения соотношения можно выразить коэффициенты 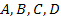 через характеристические параметры
через характеристические параметры
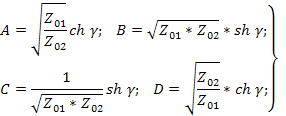
В свою очередь характеристические параметры можно определить из опытов холостого хода и короткого замыкания. Действительно, из формул получим

Для симметричного четырехполюсника характеристическое сопротивление равно среднему геометрическому из 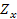 и
и 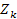

Полученные соотношения составляют основу классической теории фильтров.
Электрическое моделирование
Любая модель определенный образом изображает процесс или поведение объекта и служит для его изучения. В науке и технике используют различные методы моделирования: натурный эксперимент, физическое моделирование, модели прямой аналогии, машинное моделирование на аналоговых и цифровых вычислительных машинах, математическое моделирование и др.
Электрическое моделирование относиться к методам прямой аналогии, при котором математическое описание соответственных величин натуры и модели, различной физической природы (механической, тепловой и других), выполняется аналогичным математическими зависимостями. Электрическая модель прямой аналогии имитирует на основе аналогии натурную физическую (неэлектрической природы) по её элементам, так что каждому из физических элементов натуры в электрической модели соответствует определенный изображающий его элемент – аналог. Преимущества электрических моделей заключается в удобстве изменения параметров, простоте их регистрации физической наглядности, разработанности математического аппарата и синтеза.
В отличие от машинного моделирования при электрическом моделировании расчленяется на компоненты не математическое описание операций, а сама исследуемая система. Элементной базой электрического моделирования физических линейных систем с постоянными коэффициентами служат ранее рассмотренные элементы базового набора электрических цепей (см. табл. 1). Добавление нелинейных электрических элементов и операционных усилителей позволяет в принципе существенно расширить круг рассматриваемых задач, выходящих за пределы настоящего пособия; не затрагиваются здесь также вопросы аппаратурой реализации электрического моделирования.
По сути дела мы ограничимся лишь схемотехникой электрического моделирования, т.е. составлением эквивалентных электрических схем для физических систем различной природы с целью определения динамического поведения систем.
Исходные положения метода электрического моделирования заключаются в следующем. Для ряда систем можно установить изоморфизм – взаимооднозначное соответствие между динамическими свойствами физической системы с сосредоточенными параметрами и направленным линейным графом. На основе такого изоморфизма оказывается возможным построить эквивалентные схемы различных физических систем. Ограничимся далее рассмотрением линейных систем, модулируемых планарными цепями.
Физическая система расчленяется на простые составные части (компоненты) или элементы, т.е. заменяется эквивалентной (по изучаемым свойствам) физической цепью дискретных элементов, характеризуемых определенными параметрами. Динамические свойства элементов цепи описываются математическими соотношениями между выбранными скалярными переменными.
Для выбора переменных используем термодинамический подход. Величины, которые определяют состояние системы в термодинамическом равновесии, называется параметрами системы. Число независимых параметров равно числу путей, которым к системе можно подвести энергию в любой форме. Каждой форме энергетического контакта соответствуют два термодинамических параметра, которые имеют различных характер. Интенсивными называются параметры, величина которых не зависит от размера системы, они в термодинамическом равновесии имеют одно значение во всем объеме вещества и их значения не меняются при делении системы на подсистемы. Вторым типом параметров являются экстенсивные параметры: их значения зависят от количества вещества в системе. Таким образом, каждой форме энергетического контакта системы с окружающей средой соответствует одна пара параметров, одни из которых является интенсивным, а другой – экстенсивным, но только одни из этих параметров является независимым. Указанным условиям удовлетворяет выбор параметров, показанный в табл. 5(первая и вторая колонки).
Параметры первого типа (α) играют роль действующих сил, а второго (β) – координат состояния (зарядов) соответствующих систем. Поскольку нас интересует описание динамического поведения систем, необходимо образовать переменные, которые бы отражали это динамическое поведение. Таковыми являются «потоки» (11), вызванные соответствующими «силами» 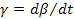 , т.е. «потоки» образуются диффиринцированием «координат» по времени (см. третью колонку табл. 5). Интегрирование соответствующих «сил» приводит к «импульсам»
, т.е. «потоки» образуются диффиринцированием «координат» по времени (см. третью колонку табл. 5). Интегрирование соответствующих «сил» приводит к «импульсам» 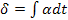 ( четвертая колонка табл. 5), производные от импульсов по потокам
( четвертая колонка табл. 5), производные от импульсов по потокам  – индуктивные параметры (шестая колонка табл.5) и производные от потенциалов по потокам
– индуктивные параметры (шестая колонка табл.5) и производные от потенциалов по потокам 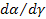 – резистивные параметры (седьмая колонка табл.5). Величины, отмеченные в табл. 5 звездочкой, введены по указанным формальным принципам.
– резистивные параметры (седьмая колонка табл.5). Величины, отмеченные в табл. 5 звездочкой, введены по указанным формальным принципам.
Анализ табл.5 показывает, что выбранные переменные совместны друг с другом, так как произведение переменных в двух первых колонках для соответствующих систем дает работу или энергию, а в первой и третьей – мощность 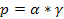 (восьмая колонка табл.5). Кроме того, очевидна аналогия указанных систем с электрическими цепями. Необходимо иметь в виду, что при данном выборе переменных анализ ограничивается только «прямыми» с точки зрения термодинамики необратимых процессов эффектами и хотя соответствующая трансформация переменных позволяет перейти к уравнениям Онзагера, последние здесь рассматриваться не будут.
(восьмая колонка табл.5). Кроме того, очевидна аналогия указанных систем с электрическими цепями. Необходимо иметь в виду, что при данном выборе переменных анализ ограничивается только «прямыми» с точки зрения термодинамики необратимых процессов эффектами и хотя соответствующая трансформация переменных позволяет перейти к уравнениям Онзагера, последние здесь рассматриваться не будут.
Переменные первого типа α (интенсивные величины) подчиняются топологическим законам, аналогичным 2-му Кирхгофа, а переменные второго 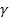 (потоки экстенсивных величин) 1-му закону Кирхгофа:
(потоки экстенсивных величин) 1-му закону Кирхгофа:
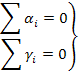
Поэтому расчет систем различной физической природы сводится к расчету аналогичных электрических цепей.
Таблица 5
| Система | Переменные величины | Параметры | Мощность | |||||
| Интенсивные α | Экстенсивные β | 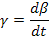
| 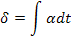
| Емкостной 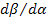
| Индуктивный 
| Резистивный 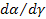
| 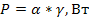
| |
| Электрическая (Э) | U,[Вт] | q,[Кл] | 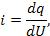 [A]
[A]
| 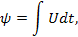 [Вб]
[Вб]
| 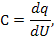 [Ф]
[Ф]
| 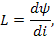 [Гн]
[Гн]
| 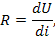 [Ом]
[Ом]
| 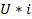
|
| Механическая поступательная (М) | f, [Н] | x, [М] | 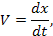 [м*с-1]
[м*с-1]
| 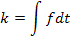 [кг*м*с-1]
[кг*м*с-1]
| 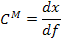
| 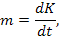 [кг]
[кг]
| 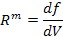
| f *V |
| Механическая вращательная | М, [Н*м] | φ, [рад] | 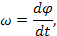 [рад*с-1]
[рад*с-1]
| 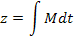
| 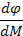
| 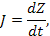 [кг*м2]
[кг*м2]
| 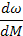
| M *ω |
| Гидравлическая (Г) Акустическая (А) | Р, [Па] | V,
[ 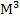 ] ]
| 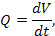 [м3*с-1]
[м3*с-1]
| 
| 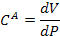
| 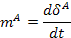
| 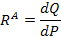
| P*Q |
| Тепловая (Т) | Т, [К] | S, [Дж*К-1] | 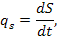 [Вт*К-1]
[Вт*К-1]
| 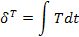
| 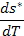
| 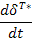
| 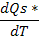
| T*Q/s |
| Диффузионная (Д) | μ [Дк*кмоль] | N, [кмоль] | 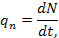 [кмоль*с-1]
[кмоль*с-1]
| 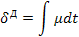
| 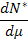
| 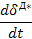
| 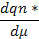
| μ*qn |
Существует одна особенность, связанная с топологическим моделированием механических систем. Для всех систем, кроме механических, принято элементы систем при образовании цепей соединять «проводниками» (электрические провода, звукопроводы, трубопроводы и т.д.). При начертании условных схемы цепей на плоскости ей соответственно приписывают свойства идеального «изолятора» (электрический изолятор, теплоизолятор, непроницаемая среда и т.д.). В механике же, наоборот, плоскость чертежа абсолютно податлива («проводима»), а соединительные элементы абсолютно твердые тела («механические изоляторы»). На «языке» электрических аналогий во всех системах, кроме механических поступательного и вращательного движения, плоскость, на которой изображается схема цепи, имеет бесконечное сопротивление Zn =∞ или нулевую проводимость, а проводники, соединяющие элементы цепей, имеют, напротив Z=0. Поэтому механические системы типологически дуальны всем остальным: плоскость чертежа имеет Zn=0, тогда как соединительные стержни являются абсолютно твердыми телами, не деформируемы и, следовательно, Zn =∞, т.е. изображаются в дуальном базисе. Учитывая это, для построения электрических аналоговых цепей для механических систем необходимо вначале построить электрическую цепь, пользуясь аналогией дуальной к вышеприведенной: 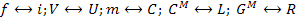 .
.
В этой системе для механического узла  , а для механического контура
, а для механического контура 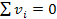 . В механической системе с поступательным движением базовыми элементами являются: источники сил, упругий элемент, элемент сопротивления, элемент массы, причем масс имеет вторым «полюсом» связь с системой координат. Пример построения аналоговых электрических цепей для простейших механических систем показан на рис.27 и 28. Последовательность построения такова. Изображается кинематическая схема системы (рис.27 а и 28а), затем механическая цепь, моделирующая систему (рис.27б и 28б), для механической цепи в соответствии с дуальной аналогией строиться электрическая цепь (рис.27 в , 28 в). Построение электрических дуальных цепей (рис.27 г и 28 г) завершает процедуру.
. В механической системе с поступательным движением базовыми элементами являются: источники сил, упругий элемент, элемент сопротивления, элемент массы, причем масс имеет вторым «полюсом» связь с системой координат. Пример построения аналоговых электрических цепей для простейших механических систем показан на рис.27 и 28. Последовательность построения такова. Изображается кинематическая схема системы (рис.27 а и 28а), затем механическая цепь, моделирующая систему (рис.27б и 28б), для механической цепи в соответствии с дуальной аналогией строиться электрическая цепь (рис.27 в , 28 в). Построение электрических дуальных цепей (рис.27 г и 28 г) завершает процедуру.
Для всех остальных физических систем построение аналогичных электрических цепей проводится непосредственно по упрощенным схемам систем. На рис.29 показан пример построения фильтра низких частот для различных систем: рис.29 а, б – механические системы; рис.29 в – гидравлическая система; рис.29 г – акустическая система; рис.29 д – механическая цепь; 29 е, ж – электрические аналоги.
Таким образом, электрическое моделирование позволяет использовать методы теории электрических цепей для расчета систем различной физической природы, что находит применение при анализе и синтезе элементов и систем электроавтоматики, в которых часто с электрической подсистемой сопрягаются подсистемы механическая, тепловая, пневматическая и другие.
Линейные цепи с распределенными параметрами.
Рассмотрим установившейся режим в системе, которая обладает равномерно распределенными линейными параметрами. Задача, связанная с анализом подобных систем, возникает, как только длительности сигналов оказываются настолько малыми (а частоты столь высокими), что длина электромагнитной волны становиться соизмерима с линейными размерами систем. Для того, чтобы показать основное отличие данного класса задач от задач анализа электрических цепей с сосредоточенными постоянными и не слишком усложнять математическую трактовку рассмотрим однородную линию передачи сигналов. Конкретно это может быть двухпроводная линия, коаксиальны кабель и т.п. Подобную систему характеризуют четыре постоянные погонные параметра, т.е. параметры, отнесенные к единицам длины: 1) последовательное линейное сопротивление 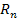 , Ом/м; 2) параллельная проводимость (проводимость утечки между проводами) Gn, См/м ; 3) последовательная индуктивность
, Ом/м; 2) параллельная проводимость (проводимость утечки между проводами) Gn, См/м ; 3) последовательная индуктивность 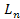 , Гн/м; 4)параллельная емкость между проводами
, Гн/м; 4)параллельная емкость между проводами 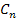 , Ф/м.
, Ф/м.
Напряжение и ток в линии являются теперь функциями двух независимых переменных : пространственной координаты x, определяющей место наблюдения сигнала, и времени t, определяющего момент наблюдения. Направление координатной оси выбирается совпадающим с направлением линии и отсчитываемым от ее начала. Задача анализа заключается в нахождении пространственно–временного распределения тока в линии 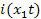 и напряжения между проводами
и напряжения между проводами 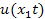
Расчетная схема элементарного участка линии показана на рис.30 а.
Пусть  и
и 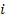 есть напряжение и ток в линии в точке с координатой x в момент t, тогда в точке с координатой (
есть напряжение и ток в линии в точке с координатой x в момент t, тогда в точке с координатой ( 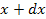 ) в тот же момент времени значения этих перменных (с точностью до бесконечно малых величин высших порядков, чем
) в тот же момент времени значения этих перменных (с точностью до бесконечно малых величин высших порядков, чем 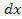 ) будут равны:
) будут равны:
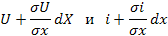
Из закона Ома для этого участка изменение напряжения равно
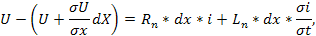
т.е. 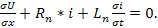
Аналогично (или из свойства дуальности) изменение тока на этом участке равно
Полученные уравнения образуют систему двух уравнений с частными производными первого порядка. Из них легко исключить любую неизвестную функцию путем частного дифиринцирования одного уравнения по x, а второго по t. После решения новой системы уравнений можно получить два телеграфных уравнения:
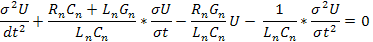
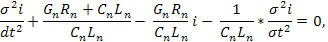
описывающих электромагнитные процессы в длинной линии, Уравнения относятся к классу гиперболических уравнений математической физики, для их решения требуется задание как начальных, так и граничных условий для напряжения и тока. Для установившегося режима уравнение (94) превращается в обыкновенное дифиринциальное уравнение. Например, для установившегося синусоидального режима из уравнения, перейдя к комплексным изображениям, получим
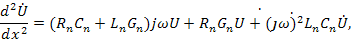
откуда, после преобразований, находим
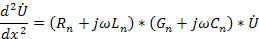
и из выражения аналогично определяем
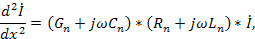
Если обозначить через 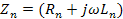 комплексное сопротивление линии на единицу длины, а через
комплексное сопротивление линии на единицу длины, а через  – комплексную проводимость на единицу длины, то уравнения примут вид
– комплексную проводимость на единицу длины, то уравнения примут вид
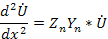
и
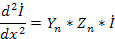
Разумеется, в общем случае, здесь величина 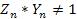 , а связана с постоянной распространения
, а связана с постоянной распространения
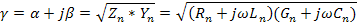
В установившемся синусоидальном режиме уравнения также превращаются в обыкновенные дифференциальные уравнения:
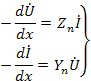
Для конечных приращений эта система в соответствии со схемой на рис.30 б, примет вид
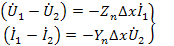
Кроме того, надо учесть, что нагрузкой данного элемента служит характеристическое сопротивление линии ZO, поэтому систему (104) надо дополнить уравнением 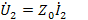 .
.
Сигнальный граф в соответствии с полученной системой для отрезка линии передачи показан на рис.30 в. Из сигнального графа находим
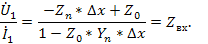
Определим характеристическое сопротивление  , Ом, как сопротивление линии в точке, бесконечно удаленной от приемного конца.
, Ом, как сопротивление линии в точке, бесконечно удаленной от приемного конца.
Поскольку входное сопротивление  должно равняться характеристическому (волновому) Z0, из формулы (106) найдем
должно равняться характеристическому (волновому) Z0, из формулы (106) найдем
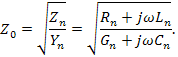
В случае распределенной механической системы – механической длинной линии с распределенной на единицу длины массой mn=m/l, податливостью (обрат упругости) Cn=Cm/l и потерями Gn=Gm/l – система будет представлять бесконечную цепочку из указанных элементов (рис.31 а). Переходя к механической моделирующей цепи (рис. 31 б) и к электрической модели(рис.31 в) и затем к дуальной цепи, получим длинную линию (рис.31 г) без сопротивления проводов Rn=0. Из уравнения для электрической длинной линии при Rn=0, заменяя i=dq/dt, найдем

где  скорость распространения электромагнитных волн в линии.
скорость распространения электромагнитных волн в линии.
Используя электромеханическую аналогию (табл. 5), из последнего уравнения, приняв 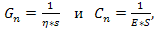
где η – коэффициент вязкости среды;
E – модуль Юнга среды;
S – площадь поперечного сечения, получим волновое уравнение для линейной вязкоупругой среды, описываемой реологической моделью Максвелла, дополненной элементом инерции (массы):
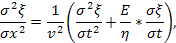
где  - фазовая скорость волны;
- фазовая скорость волны;
ξ – смещение частиц в волне.
Аналогично можно рассмотреть не продольные, а сдвиговые колебания и волны в линейных вязкоупругих средах. Проведенный анализ показывает, что реологические одномерные задачи линейной вязкоупругой среды сводятся к задачам линейных электрических цепей с сосредоточенными или распределенными постоянными, в случае волнованных задач известные реологические модели следует дополнить элементом массы (аналогично тому, как это сделано для модели Максвелла на рис.31 а)
Механические (акустические) линии на ультразвуковых частотах совместно с пьезо-или магнитно-стрикционными преобразователями часто используют как элементы временной задержки (линии задержки) электрических сигналов.
Дата добавления: 2015-10-13; просмотров: 4491;
