Матрично-топологические методы
После перехода от реальной физической системы к моделирующей ее электрической цепи, а от последней к схеме замещения, составленной из элементов базового набора, задача анализа заключается в нахождении токов и напряжений в каждом элементе, исходя из которых определяются все остальные необходимые характеристики схемы в целом.
При анализе схем с помощью ЭВМ (машинном анализе) в машину вводится информация, содержащая табличное описание схемы (перечень элементов, их параметры и способ соединения), режим анализа (статический, динамический) и перечень характеристик, подлежащих определению. Программа должна обеспечивать автоматизацию процессов анализа конфигурации схемы, составление системы линейно-независимых уравнений цепей, их решение в требуемых режимах и вывод результатов анализа.
Указанные задачи решаются с помощью матрично-топологических методов, основанных на теории графов и матричной алгебре. Конфигурация схемы представляется с помощью топологических матриц, на основании которых составляются векторно-матричные уравнения цепей. Параметры элементов схем представляют в виде параметрических матриц, которые используются для составления матричных уравнений, отражающих соотношения токов и напряжений элементов. Полученная система матричных уравнений решается соответствующими численными методами. В настоящем пособии разумеется не ставится задача подробного и математически строгого топологического машинного анализа, а скорее - введение в круг задач и формулировка основных понятий.
В основе топологических (геометрических) свойств цепей лежат два закона Кирхгофа, из которых видно, что топологические свойства цепей не зависят от тока и свойств элементов ее составляющих.
Если ветви электрической схемы (рис.15 а) заменить отрезками (дугами) произвольной длины и формы, а точки их соединений (узлы)-вершинами, т0 получившаяся геометрическая фигура (диаграмма) называется ненаправленным неориентированным графом электрических цепей (рис.15 б). Если на ветви графе нанести направления токов (напряжений) в вине стрелок, то получится ориентировочный, граф или орграф (рис. 15 в). Для удобства расчетов на ветвях орграфа указывают параметры в соответствии со схемой цепи (рис.15 в). Любую совокупность ветвей и вершин, принадлежащих графу, называют подграфом. Любой замкнутый путь, позволяющий выйти из вершины графа и вернуться в нее, не проходя дважды по одной ветви и не пересекая дважды одну и ту же вершину, называется контуром.
Подграф, содержаний все вершины графа и не содержащий ни одного контура, называется фундаментальным деревом графа, которое для краткости будет называться далее просто деревом (выделено двойными линиями на рис.15в).
Ветви графа, вошедшие в дерево, называются ветвями дерева или ребрами, а не вошедшие - хордами или ветвями связи. Совокупность хорд образует дополнение дерева. Если обозначить число вершин (узлов) графа через 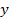 , число всех ветвей - через
, число всех ветвей - через 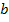 , число ребер - через р, а число хорд - через
, число ребер - через р, а число хорд - через 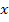 , то они связаны соотношениями:
, то они связаны соотношениями:

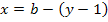
Для одного и того же графа можно построить много деревьев в зависимости от выбора начальной вершины. Часть из них будут изоморфными (отличаются только нумерацией вершин).
Граф схемы можно не только начертить, но и записать аналитически в виде таблицы, называемой матрицей соединений (инциденций). Число ее строк равно числу узлов (вершин графа), а число столбцов – числу ветвей. Каждый элемент 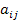 матрицы равен – I, если j-я ветвь входит в i-й узел, +I, если выходит 0 если она не соединена j-м узлом. Для получения линейно независимой системы вычеркивают одну из строк, обычно соответствующую базисному узлу, образующаяся при этом матрица A размером
матрицы равен – I, если j-я ветвь входит в i-й узел, +I, если выходит 0 если она не соединена j-м узлом. Для получения линейно независимой системы вычеркивают одну из строк, обычно соответствующую базисному узлу, образующаяся при этом матрица A размером 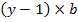 называется матрицей узлов. Общая структура матрицы A и ее содержание для графа на рис.15 (в) показаны в табл.4. Матрица A может быть представлена как совокупность подматриц:
называется матрицей узлов. Общая структура матрицы A и ее содержание для графа на рис.15 (в) показаны в табл.4. Матрица A может быть представлена как совокупность подматриц:
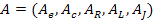
| Матрица A | ||||||||
| Подматрицы A | AE | AR | AC | AL | AJ | |||
| Ветви | E | R1 | R2 | R3 | C1 | C2 | L | J |
| Узел 1 Узел 2 Узел 3 Узел 4 | -I +I 0 0 | 0 -I +I 0 | -I 0 0 0 | 0 0 -I +I | 0 0 0 -I | 0 0 -I +I | 0 0 0 -I | +I 0 0 0 |
Кроме матрицы узлов , для описания топологии используют матрицы главных сечений и главных контуров. Сечением называется любая минимальная совокупность ветвей, при удалении которых граф распадается на два подграфа.; Сечение можно наглядно изобразить в виде следа некоторой замкнутой поверхности Si , однократно рассекающей соответствующие ветви; часть графа, заключенную внутри сечения называют обобщенным узлом. Главным сечением называется сечение, одна из ветвей которого есть ребро, а остальные ветви-хорды (например сечение S1 , отмеченное пунктиром на рис.15 в). Главным контуром называется контур, образующийся при подключении хорды к дереву графа.
Очевидно, что число главных сечений равно числу pебep, т.е. 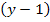 , а число главных контуров – числу хорд, т.е. b-y-1. Матрица главных сечений Q – это прямоугольная таблица размером
, а число главных контуров – числу хорд, т.е. b-y-1. Матрица главных сечений Q – это прямоугольная таблица размером 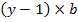 , строки которой соответствуют главным сечениям, а столбцы – ветвям графа. Каждый элемент qij этой матрицы равен +I, если j - я ветвь входит в i-е сечение со знаком «+», равен –I, если со знаком « - » и 0, если не входит; при этом за положительное направление ветви в сечении принимается направление ветви дерева этого сечения.
, строки которой соответствуют главным сечениям, а столбцы – ветвям графа. Каждый элемент qij этой матрицы равен +I, если j - я ветвь входит в i-е сечение со знаком «+», равен –I, если со знаком « - » и 0, если не входит; при этом за положительное направление ветви в сечении принимается направление ветви дерева этого сечения.
Матрицей главных контуров B называется таблица размеров 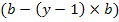 , строки котрой соответствуют главным контурам, а столбцы – ветвям графа. Каждый элемент bij этой матрицы равен + 1 , если направление ветви совпадает с направлением обхода контура, -1— при противоположном направлении и 0, если ветвь не входит в контур. За направление контура выбирают направление хорды (ветви связи) этого контура.
, строки котрой соответствуют главным контурам, а столбцы – ветвям графа. Каждый элемент bij этой матрицы равен + 1 , если направление ветви совпадает с направлением обхода контура, -1— при противоположном направлении и 0, если ветвь не входит в контур. За направление контура выбирают направление хорды (ветви связи) этого контура.
С помощью топологических матриц можно сформулировать законы Кирхгофа для электрических цепей в матричной форме. Обозначим через
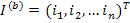
столбцовую матрицу токов всех ветвей, тогда уравнение
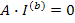
представляет матричную запись I-го закона Кирхгофа. Если обозначить через
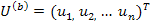
столбцовую матрицу напряжений ветвей, то уравнение
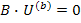
представляет матричную запись 2-го закона Кирхгофа. Соответственно уравнение
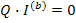
представляет запись 1-го закона Кирхгофа для обобщенных узлов. Если обобщенные узлы совпадают с простыми узлами схемы, то
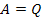
Дуальными называют два графа, если узловая матрица одного их них A1 равна контурной матрице B2 другого (и наоборот):
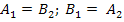
Отсюда следует свойства дуальности электрических схем и правила построения дуальных цепей, отмеченные ранее.
С помощью матрицы A можно выразить напряжение всех ветвей через потенциалы узлов, если ввести столбцовую матрицу потенциалов узлов
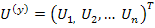
то
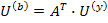
Где A – транспортировочная узловая матрица, а потенциалы узлов Ui отсчитываются относительно базисного угла. Если матрицу напряжений ветвей дерева обозначить через U(д), то
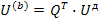
Т.е. напряжение любой ветви схемы можно определить через напряжение ветвей дерева.
Если ветвям дерева присвоены первые номера, то матрица главных сечений может быть разделена на две подматрицы:
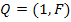
Где 1 – единичная подматрица порядка 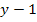 , столбцы которой соответствуют ветвям дерева; F – подматрица, столбцы которой соответствуют ветвям связи.
, столбцы которой соответствуют ветвям дерева; F – подматрица, столбцы которой соответствуют ветвям связи.
Токи всех ветвей могут быть выражены как линейные комбинации токов ветвей связи, можно вывести контурный ток, равный току ветви связи этого контура, тогда
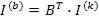
Где 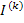 – столбцовая матрица контурных токов.
– столбцовая матрица контурных токов.
Если ветвям дерева присвоены первые номера, то матрица главных контуров состоит из двух подматриц:
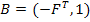
Следует подчеркнуть, что матрицы Q и B записаны для главных сечений и главных контуров, соответствующих одному и тому же дереву; единичные подматрицы в них имеют разный порядок: 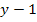 - в матрице Q и
- в матрице Q и 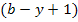 – в матрице B.
– в матрице B.
При практической решении задачи матрично-топологическими методами каждую ветвь K (рис.16) графа схемы представляют обобщенной ветвью, образованной двухполюсником Yk или
Zk и двумя источниками: напряжения Ėk и тока 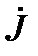 k . Тогда из закона Ома уравнение, описывающее эту ветвь будет иметь вид
k . Тогда из закона Ома уравнение, описывающее эту ветвь будет иметь вид
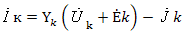
Используя уравнение
A·I=0
Находим
A·Y·U=A(J-Y·F)
И далее, подставляя
U=AT·U(y)
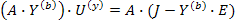
Назовем матрицей узловой проводимости

Тогда
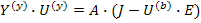
Узловое напряжение равно
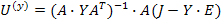
После того как найдено U(y) можно по уравнению найти U(b) и далее ток любой ветки 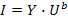 .
.
Проведенный анализ носит название узлового. Используя свойство дуальности можно провести контурный анализ. Из уравнения
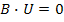
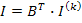
И уравнения обобщенной ветви в виде
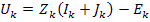
Получим
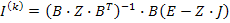
Это векторно-матричное уравнение относительно всех контурных токов (токов связей графа), представляющее собой в развернутом виде систему из 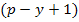 интегро-дифференциальных уравнений. При получении графа из схемы цепи требуется закорачивать источники напряжений и разрывать ветви с источниками тока, а ветви с идентичными источниками преобразовать специальными приемами или соблюдать приоритет (иерархию) формирования матриц по столбцам в виде правила
интегро-дифференциальных уравнений. При получении графа из схемы цепи требуется закорачивать источники напряжений и разрывать ветви с источниками тока, а ветви с идентичными источниками преобразовать специальными приемами или соблюдать приоритет (иерархию) формирования матриц по столбцам в виде правила
Дерево
E, C, R, L, J
Дополнение
Таким образом, ветви с источниками напряжения должны быть в дереве графа, а с источниками тока - в его дополнении, т.е. являться хордами (см. рис.15 в и табл.4).
Матрица проводимости ветвей Y становится недиагональной, если в схеме имеются управляемые напряжением источники тока и при наличии индуктивных связей.
Полученные уравнения (25), (27) неудобны для численного решения и в случае линейных уравнений их сводят к системе линейных алгебраических уравнений с помощью преобразований Фурье или Лапласа.
При условии, если R, C, L - элементы являются нелинейными, зависящими от напряжений и токов в них, то их параметры выражаются частными производными соответствующих функций.
При анализе переходных характеристик численными методами решения уравнений вся длительность переходного процесса рассматривается состоящей из большого количества интервалов времени.
Основным недостатком рассмотренных методов анализа цепей является необходимость обращения параметрических матриц вида 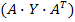 или
или 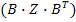 Известно, что из всех операций над матрицами обращение матриц является наиболее трудоемкой, требующей больших затрат времени. Поэтому в настоящее время разработаны более эффективные в общем случае динамического анализа сложных нелинейных схем методы: метод переменных состояния с использованием мал их ( ЭВМ и дифференциально-конечный метод, ориентированный на ЭВМ третьего поколения.
Известно, что из всех операций над матрицами обращение матриц является наиболее трудоемкой, требующей больших затрат времени. Поэтому в настоящее время разработаны более эффективные в общем случае динамического анализа сложных нелинейных схем методы: метод переменных состояния с использованием мал их ( ЭВМ и дифференциально-конечный метод, ориентированный на ЭВМ третьего поколения.
Дата добавления: 2015-10-13; просмотров: 1478;
