Моделирование транспортных систем. Потоки в сетях

Одно из основных приложений сетей — моделирование транспортных систем, по которым перемещаются люди, автомобили, корабли, транспортируют грузы, жидкие продукты и т.д. В данных моделях пункты, в которых происходит изменение потоков транспортируемых объектов — населенные пункты, станции, точки ветвления либо слияния — отмечают вершинами. Те части систем, по которым происходит само пространственное перемещение объектов (участки трубопроводов, линии электропередач, дороги, каналы) отображают взвешенными ориентированными ребрами (дугами). Вес означает предельную пропускную способность данного участка системы.

Обычно в графовых моделях транспортных систем рассматривают два полюса: источник v_и (входная вершина, которая не имеет входящих дуг, а только исходящие) и сток v_с (выходная вершина, в которую дуги только входят). Все остальные вершины — внутренние. Им инцидентны как входящие, так и выходящие дуги. Множество входящих дуг внутренней вершины V_i обозначим через D⁺(V_i), множество выходящих дуг — через D⁺(V_i).

Графовая модель транспортной системы может быть представлена в виде взвешенной ориентированной двухполюсной сети Г = ({v_и , v_с}, V, X, D), у которой веса дуг заданы матрицей весов D. На рис. 1.15 показана графовая сетевая модель простейшей транспортной сети. Веса проставлены непосредственно на дугах сети.

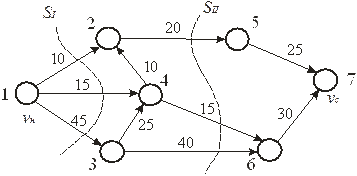
Рис.1.15. Сетевая модель транспортной системы

Для сетевых моделей транспортных систем вводятся специальные понятия, характеризующие их пропускную способность.

Определение. Неотрицательное отображение j, заданное на множестве дуг сети, называют потоком, если оно удовлетворяет двум условиям:

1) для каждой дуги сети х = (V_i, V_j ): j(х)=j _ij=j (V_i, V_j ) £ d_ij,

2) для каждой внутренней вершины сети V_i :

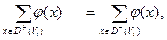
3) для источника v_и и стока сети v_с. :

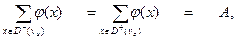
где А — количество продукта, подаваемого через источник в сеть и выходящего из ее стока, называемое суммарным потоком в сети (потоком в сети). Максимально возможную его величину сокращенно называют максимальным потоком в сети.

Физически поток обычно означает количество продукта, передаваемого по выделенному участку транспортной системы за единицу времени. Первое условие выражает ограниченность пропускной способности рассмотренного участка. Второе — неразрывность потока во внутренних вершинах, передаваемый продукт в них не появляется и не исчезает. Третье означает отсутствие потерь и добавок продукта при его передаче по сети в целом —сколько продукта поступает в источник, столько же удаляется из стока.

Определение. Если для дуги сети х = (V_i, V_j )выполняется условие d_ij = j _ij , то данную дугу называют насыщенной. Если выполняется условие d_ij > j _ij , то дугу называют ненасыщенной, а величину (d_ij - j _ij) — остаточной пропускной способностью дуги.

Для оценки потока в сети используют понятие разреза.

Определение. Множество дуг сети, удаление которых разрывает все цепи в ней таким образом, что начала всех дуг лежат в одной части сети, а концы — в другой, называют разрезом. Разрез можно указать путем перечисления дуг {(V_i, V_j )}, образующих его. Обозначим разрез через S{(V_i, V_j )}. Пропускной способностью Р(S{(V_i, V_j)}) разреза S{(V_i, V_j)} называют сумму пропускных способностей дуг{(V_i, V_j )}, образующих его:

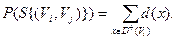
Разрез с минимальной пропускной способностью называют минимальным.

В сетевой модели транспортной системы на рис.1.15. показаны разрезы, обозначенные S_Iи S_II. Как следует из рисунка,

Р(S_I ) = Р({(V₁, V₂); (V₁, V₃); (V₁, V₄)}) = 10 +15 + 45 = 70,

Р(S_II ) = Р({(V₂, V₅); (V₃, V₆); (V₄, V₆)}) = 20 + 40 +15 = 75.

Связь максимального потока в сети с разрезами устанавливает

Теорема 1.2. Форда—Фалкерсона.В любойвзвешенной ориентированной двухполюсной сети Г = ({v_и , v_с}, V, X, D) максимальный поток в сети равен пропускной способности ее минимального разреза.

Рассмотрим свойства потоков в сетях, которые используют при построении общих алгоритмов определения максимального потока в сети. Пусть М — произвольный маршрут в сети от источника к стоку, состоящий из вершин (v_и , V_i1, V_i2,… , V_ik, v_с) . Очевидно, его пропускная способность равна минимальному из весов дуг, составляющих маршрут:

А(М) = min {d_и,i1, d_i1,i2, … , d_ik,_с}.

Если вычесть данный предельный поток А(М)из общей пропускной способности сети, то все дуги (V_i, V_j) , входящие в маршрут М, будут иметь остаточную пропускную способность (d_ij - А(М)). При этом дуги с нулевой остаточной пропускной способностью (d_ij - А(М)=0)могут быть исключены из сети, поскольку их пропускная способность использована полностью.

Решение. Максимальная пропускная способность М₁ равна:

А(М₁) = min {d₁₂, d₂₅, d₅₇}= min {10, 20, 25}=10.

Если учесть поток величиной А(М₁)=10по сети в целом, дугам, входящим в М₁, необходимо присвоить новые (остаточные) пропускные способности:

d₁₂¢= d₁₂ - 10 = 0, d₂₅¢= d₂₅ - 10 = 10, d₅₇¢= d₅₇ - 10 = 15.

При этом дугу (V₁, V₂) с нулевой остаточной пропускной способностью можно из общей сети исключить.

Ответ: А(М₁)=10. d₁₂¢= 0, d₂₅¢=10, d₅₇¢=15.

Данное свойство лежит в основе всех алгоритмов расчета максимального потока. Рассмотрим его простейший вариант.