Алгоритм Шимбелла
Алгоритм предназначен для определения кратчайших расстояний между всеми парами вершин взвешенного графа и учитывает число ребер, входящих в соответствующие простые цепи. Матрица весов D в исходном виде задает стоимость переходов между вершинами графа по цепям, состоящим из одного звена.Для анализа переходов длины 2 и выше в методе используются соответствующие степени матрицы D специального вида. Элементы dij k+1 матрицы D k+1, задающие минимальную стоимость перехода длины (k+1) от вершины Vi к вершине Vj, определяют в результате умножения матрицы D на матрицу D k по специальному правилу:
dij k+1 = min¢ {(di1 +¢ d1j k), (di2 +¢ d2j k), … , (din +¢ dnj k)},
где:
1) в операции попарного суммирования элементов «+¢» при наличии хотя бы одного нулевого значения вся сумма принимается равной нулю,
2) операция «min¢» означает выбор минимального ненулевого элемента списка. Нулевые значения в расчет не принимаются.
Степени матрицы D k+1 для графа будут также симметричны, как и D, однако на главной диагонали у них будут появляться ненулевые элементы.
Кратчайшая цепь между вершинами графа с n вершинами может включать не более (n–1) ребер, иначе цепь будет содержать циклы и ее можно сократить. Предельное число ребер (n–1) в кратчайшем пути достигается, например, между вершинами V1и Vn в графе, представляющем одну простейшую цепь (рис.2.5):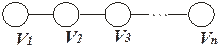
Рис.2.5. Связный граф с n вершинами в виде одной цепиПоэтому искомое кратчайшее расстояние между заданной парой вершин Vi и Vj в общем случае определяется как минимальное из значений элементов dij, dij 2, dij 3, … , dij n-1, соответствующих матрице D и ее степеням D 2, D 3, …, D n-1. Пример 1. Для графа с 5 вершинами, данного на рис.2.4, найти по методу Шимбелла степени D2, D3, D4 матрицы весов D. Определить кратчайшее расстояние между вершинами V1и V2 .Решение.В исходной матрице весов D расстояние d12 = 30 и соответствует ребру графа V1V2 .Найдем степени D. Проиллюстрируем применение правил умножения матриц в методе Шимбелла на примере вычисления элемента dij 2 в степенной матрице D 2.d12 2 = min¢ {(d11 +¢ d12), (d12 +¢ d22), (d13 +¢ d32), (d14 +¢ d42), (d15 +¢ d52)} = min¢ {(0 +30), (30 + 0), (0 + 0),(20 + 30),(10 + 15)}= min¢ {(20 + 30),(10 + 15)}=25.Применяя данное правило, получим следующие степени матрицы весов D: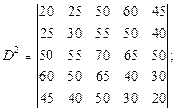 
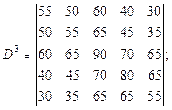
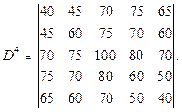Ответ: из равенств d12 = 30, d122 = 25, d123 = 50, d124 = 45 следует, что минимальным будет один из путей, состоящих из двух ребер. Это цепь (V1, V5 , V2 ).При определении максимальных длин маршрутов вместо операции «min¢» в алгоритме Шимбелла необходимо использовать аналогичную операцию «max¢».Метод Шимбелла прост в реализации, однако у него в процессе поиска учитывается много маршрутов, содержащих циклы, т.е. явно не оптимальных. Так в примере 1 минимальное расстояние из трех ребер d123 = 50 из V1в V3 реализуется маршрутом (V1, V3 , V1, V3), содержащим цикл (V1, V3 , V1).Сам метод позволяет лишь определять длины кратчайших путей между вершинами. Однако степенные матрицы Dk не указывают сам путь – последовательность вершин и ребер. Наборы индексов вершин в графе можно запоминать при определении элементов данных матриц.Алгоритм ДейкстрыПредназначен для определения кратчайшего расстояния от выделенной вершины Vн до всех остальных вершин взвешенного графа G = (V, X, D), у которого веса ребер неотрицательны. Также предусматривает эффективное построение самого кратчайшего пути из Vн до любой выбранной вершины графа.В алгоритме Е. Дейкстры (Голландия) использован принцип динамического программирования, предложенный Р. Беллманом (США) и заключающийся в поэтапном отбрасывании заведомо худших вариантов в процессе их перебора. В алгоритме осуществляется последовательное прохождение (посещении) вершин взвешенного графа с присвоением и последующей коррекцией меток на них, которые имеют смысл минимально известных расстояний от данных вершин до Vн . Метку вершины Vi будем обозначать М(Vi). Алгоритм включает два этапа — на первом расставляются метки и уточняется их значение, на втором строится искомый кратчайший путь.Первый этап алгоритма Дейкстры—расстановка меток.ШАГ 1. Начальные присваивания. Все вершины отмечаются, как непосещенные. Вершине Vн присваивается метка 0, всем остальным — метка «¥» (бесконечность). ШАГ 2. Выбор очередной вершины и ее обработка. Из непосещенных выбирают вершину с минимальной меткой. Обозначим ее Vм. Рассматривают все смежные с ней непосещенные вершины — «соседи». Для каждого «соседа» Vс выполняют следующие действия.1. К метке выбранной вершины Vм прибавляют вес d мс ребра (Vм, Vс) , соединяющего ее с Vс.2. Полученную сумму М(Vм) + d мс сравнивают с существующей меткой «соседа» Vс . Если М(Vм) + d мс < M(Vс), то найден более короткий путь из Vн в Vс через Vм. Это новое значение присваивают в качестве метки соседней вершине Vс: M(Vс):= М(Vм) + d мс . Иначе значение метки M(Vс)остается прежним. После обработки всех соседних с Vм вершин, она отмечается как посещенная. ШАГ 3. Проверка завершения работы первого этапа алгоритма. Если множество непосещенных вершин содержит только одну вершину, то алгоритм завершает свою работу, поскольку улучшать метки больше невозможно — у последней вершины не может быть непосещенных соседних вершин. В качестве искомых минимальных расстояний принимают текущие значения меток вершин. Если же число непосещенных вершин больше 1, то переход на ШАГ 2 и продолжение выполнения алгоритма.Пример 2. Выполнить первый этап алгоритма Дейкстры для вершины V1 взвешенногографа, данного на рис.2.4. Решение.ШАГ 1. Начальные присваивания. Множество посещенных вершин Р = Æ , множество непосещенных вершин N={1, 2, 3, 4, 5}. Метки на вершинах: М(1) = 0, М(2) = ¥, М(3) = ¥, М(4) = ¥, М(5) = ¥. I итерация. ШАГ 2. Выбираем очередную вершину из непосещенных с минимальной меткой.Это начальная вершина V1. Ее соседями являются непосещенные вершины V2, V4, V5 . Поскольку для всех соседей неравенство М(Vм) + d мс < M(Vс) выполнено, то после первой итерации: Р = {1}, N={2, 3, 4, 5}, М(1) = 0, М(2) = 30, М(3) = ¥, М(4) = 20, М(5) = 10. ШАГ 3. Поскольку ú N÷ = 4 >1, то переход на ШАГ 2 следующей итерации.II итерация. ШАГ 2. Из непосещенных вершин минимальная метка у вершины V5 . Ее выбираем в качестве следующей. С ней смежны непосещенные вершины V2, V3 . Для вершины V2: М(5) + d 25 = 10 +15 < М(2) = 30, поэтому присваиваем М(2):= 25.Для вершины V3: М(5) + d 35 = 10 + 40 < М(3) = ¥, присваиваем М(3):= 50.После второй итерации: Р = {1, 5}, N={2, 3, 4}, М(1) = 0, М(2) = 25, М(3) = 50, М(4) = 20, М(5) = 10. ШАГ 3. ú N÷ = 3 >1, переход на ШАГ 2 следующей итерации.III итерация. ШАГ 2. Из непосещенных вершин выбираем V4, поскольку у нее минимальная метка. С ней смежна непосещенная вершина V2 . Для вершины V2: М(4) + d 24 = 20 +30 > М(2) = 25, поэтому метку М(2)сохраняем.После третьей итерации:Р ={1, 5, 4}, N={2, 3}, М(1) = 0, М(2) = 25, М(3) = 50, М(4) = 20, М(5) = 10. ШАГ 3. ú N÷ = 2 >1, переход на ШАГ 2 следующей итерации.IV итерация. ШАГ 2. Из непосещенных вершин выбираем V2. С ней смежна непосещенная вершина V3 . Для вершины V3: М(2) + d 24 = 25 +35 > М(3) = 50, поэтому метку М(3)сохраняем.После четвертой итерации:Р ={1, 5, 4, 2}, N={3}, М(1) = 0, М(2) = 25, М(3) = 50, М(4) = 20, М(5) = 10. ШАГ 3. ú N÷ = 1, завершение первого этапа работы алгоритма.Ответ: в результате выполнения первого этапа алгоритма Дейкстры для взвешенногографа (рис.2.4) получены следующие значения кратчайших длин путей от вершины V1 до остальных вершин графа, которые метками указаны на рис.2.6. 
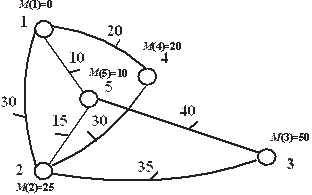Рис.2.6. Кратчайшие длины путей от вершины V1 Под бесконечностью «¥» в практических расчетах принимают реальное число, заведомо большее суммарного веса любого из путей в графе. Если такая оценка не известна из предыдущих расчетов, то в качестве ее можно принять, например, n × dmax , где n — число вершин графа, dmax — максимальный вес ребра графа.Если конечная вершина пути Vк задана заранее, то применение первого этапа алгоритма можно закончить, после того, как Vк станет посещенной. Если граф несвязный, то необходимо изменить условие завершения работы первого этапа на ШАГе 3. В этом случае работа завершается, когда у всех непосещенных вершин величины меток равны ¥ .Второй этап алгоритма Дейкстры—опеределение кратчайшего пути до заданной вершины.Допустим, для всех вершин некоторого взвешенного графа G = (V, X, D)найдены кратчайшие длины путей (метки) из вершины Vн и задана вершина Vк , в которую необходимо попасть из нее. Требуется построить цепь минимальной длины из Vн в Vк. Построение цепи начинается с конечной вершины Vк.ШАГ 1. Начальные присваивания. В качестве текущей вершины цепи Vт принимаем конечную вершину Vк. Предыдущая вершина цепи Vпр = Æ.ШАГ 2. Выбор очередной вершины цепи. Рассматривают все вершины графа, смежные с текущей вершиной цепи Vт, отличные от предыдущей вершины Vпр. Среди них выбирают такую соседнюю вершину Vс, для которой выполняется равенство: М(Vc) + d ст = М(Vт). При этом текущую вершину Vт принимают в качестве предыдущей: Vпр = Vт , а найденную соседнюю вершину считают следующей текущей: Vт = VсШАГ 3. Проверка завершения построения цепи. Если Vт = Vн, (цепь дошла до начальной вершины), то переход на ШАГ 4 для завершения работы алгоритма. Иначе — переход на ШАГ 2. ШАГ 4. Завершение работы алгоритма. После окончания итераций искомый кратчайший путь из начальной вершины Vн в конечную вершину Vк получают, записывая найденную последовательность текущих вершин в обратном порядке.Пример 3. Построить по алгоритму Дейкстрыкратчайший путь из вершины V1 в вершину V3 во взвешенном графе на рис.2.4, используя разметку вершин на рис.2.6, полученную по первому этапу алгоритма.Решение. ШАГ 1. Начальные присваивания. Текущая вершина цепи Vт = V3. Предыдущая вершина Vпр = Æ.I итерация. ШАГ 2. Выбор очередной вершины цепи. С V3 смежными являются V2 и V5. Для вершины V2: М(V2) + d 23 = 25+35 ≠ М(V3) = 50. Для вершины V5: М(V5) + d 53 = 10+40 = М(V3) = 50. Следовательно, Vпр = V3,а следующая текущаявершина Vт = V5. ШАГ 3. Проверка завершения построения цепи. V5≠ V1, следовательно, цепь не дошла до начальной вершины. Переход на ШАГ 2 и продолжение работы.II итерация. ШАГ 2. Выбор очередной вершины цепи. С текущей вершиной Vт = V5 смежными являются вершины V1 и V2 , отличные от предыдущей Vпр = V3 .Для вершины V1: М(V1) + d 13 = 0+10 =М(V5). Следовательно, Vпр = V5,а следующая текущаявершина Vт = V1. ШАГ 3. Проверка завершения построения цепи. V1= V1, следовательно, цепь дошла до начальной вершины. Завершение работы алгоритма. Ответ: записывая на ШАГе 4 полученную последовательность текущих вершин (V3, V5, V1) в обратном порядке, получим (V1, V5, V3) — искомый кратчайший путь из вершины V1 в вершину V3 во взвешенном графе на рис.2.4.Применение принципа динамического программирования позволяет значительно сократить объем вычислений. Е. Дейкстра строго доказал следующую теорему.Теорема 2.3.Алгоритм Дейкстры во взвешенном графе с неотрицательными весами ребер всегда дает кратчайший путь из начальной вершины Vн в заданную конечную вершину Vк. Кратчайший путь, определяемый по алгоритму Дейкстры, может быть одним из нескольких существующих. Недостаток метода — неприменимость при отрицательных весах ребер, которые иногда используются при решении задач. 2.2.2. Гамильтоновы цепи и циклы
Определение. Простой цикл, содержащий все вершины графа, называется гамильтоновым. Гамильтоновой цепью называется простая цепь, содержащая все вершины графа.
Очевидно, если граф имеет гамильтонов цикл, то он имеет и гамильтонову цепь, обратное верно не всегда.
Пример 4. Определить, существует ли гамильтонов цикл и гамильтонова цепь в показанном на рис.2.7 графе G = (V, X), V = (1, 2, 3, 4, 5, 6), X = ((1, 2), (1, 3), (1 ,4), (2, 3), (3, 4), (4, 5), (4, 6), (5, 6)).
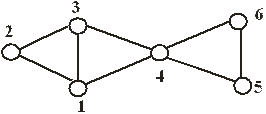
Рис.2.7
Решение. 1. Рассмотрим построение гамильтонова цикла. Допустим, он существует. В качестве начальной может быть принята любая вершина, например, V1 . При переходе от V1 к V5 и обратно вершина V4 должна быть пройдена как минимум 2 раза. Поэтому любой цикл, содержащий все вершины графа, не будет простым, ( а, следовательно, и гамильтоновым ).
2. Цепь V1V2V3V4V5V6 является гамильтоновой.
Ответ: гамильтонова цепь в данном графе G существует, а гамильтонов цикл - нет.
Аналитических критериев существования гамильтоновых цепей и циклов в графе не найдено. Доказан ряд достаточных условий, при выполнении которых граф гарантированно содержит гамильтонов цикл. Например, доказанная норвежским математиком О.Оре
Теорема 2.4. Если у связного графа G = (V, X)число вершин ú Vú = n ³ 3 и для степеней d(Vi), d(Vj) любых двух его несмежных вершин Vi и Vj выполняется условие d(Vi)+ d(Vj)³ n, то в G есть гамильтонов цикл.
У произвольных графов для выяснения существования гамильтонова цикла и его построения используют комбинаторные алгоритмы, решающие задачу методом перебора.
2.2.3. Эйлеровы цепи и циклы
Определение. Эйлеровым называют цикл, проходящий ровно один раз по всем рёбрам графа. Эйлеровой называют цепь, содержащую по одному все рёбра графа.
Критерий существования эйлерова цикла в графе дан Л.Эйлером и имеет следующий вид.
Теорема 2.5 Эйлера. Эйлеровым циклом обладают все связные мультиграфы, у которых степени всех вершин чётны.
Пример 5. Определить, существует ли эйлеров цикл и эйлерова цепь в графе G =(V,X) из предыдущего примера 4.
Решение. 1. По вышеприведенной Теореме эйлеров цикл не существует, поскольку существуют вершины с нечётными степенями вершин (V1 и V3).
2.Цепь (V1V2) (V2 V3) (V3V1) (V1 V4) (V4V5) (V5 V6) (V6V4) (V4 V3)является эйлеровой.
Ответ: эйлерова цепь в графе G существует, цикл — нет.
2.3. Раскраски графов
В ряде случаев при разработке систем требуется присвоить её элементам (либо связям) некоторые свойства таким образом, чтобы объекты с одинаковыми свойствами не взаимодействовали непосредственно между собой. Часто такое требование встречается при составлении расписаний различного рода.
В графовых моделях приписывание свойств вершинам или рёбрам условно называют раскраской, т.е. полагается, что каждому свойству соответствует свой определённый цвет.
Определение. Если смежные вершины (рёбра) графа раскра-шены в различающиеся цвета, то соответствующая вершинная (рёберная) раскраска называется правильной.
Наименьшее число цветов, требуемое для правильной раскраски (рёберной раскраски) графа G, называется хроматическим (рёберным хроматическим) числом графа G и обозначается c(G)( c¢(G) ).
По умолчанию под раскраской графа подразумевается вершинная раскраска.
Рассмотрим наиболее употребительные оценки для хроматических чисел графов. Вначале рассмотрим вершинные раскраски.
Теорема 2.6. c(G) £ n, где n — число вершин.
Доказательство. Справедливость утверждения теоремы следует из того, что раскраска вершин, при которой все они имеют различные цвета, всегда является правильной. Оценка достигается на полных графах Кn , поскольку у них все вершины смежные.
Теорема 2.7. c(G) ³ max d(C), где max d(C)—максимальная степень клик в графе G.
Доказательство. Так как клика С степени max d(C)— полный граф, то из c( С ) = max d(C)следует: c(G) ³c(С)=max d(C).
Для реберных раскрасок справедливы следующие утверждения.
Теорема 2.8. c¢ (G)£ m, где m — число рёбер.
Доказательство. При раскраске всех рёбер различными цветами условие правильности раскраски автоматически выполняется. Данная оценка достигается на звёздах с m лучами, поскольку у них все рёбра смежные.
Теорема 2.9. c¢ ( G ) ³ max d( v ), где max d( v ) — максимальная степень вершин графа G.
Доказательство. Рассмотрим в исходном графе G звезду S с центром в вершине с максимальной степенью и лучами — рёбрами, исходящими из vi. Справедливость теоремы следует из очевидных соотношений: c¢ (G) ³c¢ (S) = d(vi)= max d(v).
Пример 1. Найти хроматические числа c(G), c¢(G) и построить правильные вершинную и реберную раскраски с использованием минимальных чисел цветов для графа G = (V,X), V = (1, 2, 3, 4, 5), X = ((1, 2), (1, 5), (2, 3), (2, 5), (3, 4), (3, 5), (4, 5)), данного на рис.2.11 .
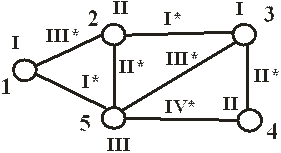
Рис.2.11. Граф к примеру 1
Решение. Из структуры графа следует: n = 5, m = 7, maxd(v) = d(V5) = 4. Максимальная степень клик графа maxd(С) = 3 (например, в клике, образованной вершинами V1, V2, V5 и рёбрами между ними).
1.Рассмотрим вершинную раскраску. Из Теорем 2.6, 2.7 следует, что maxd(С)£c(G)£ n, 3£c(G) £5. Полученная оценка показывает, что минимальное количество цветов, необходимых для правильной раскраски, лежит в интервале от 3 до 5. Поскольку правильная раскраска вершин тремя цветами (I,II,III) существует (она показана на изображении графа), то отсюда следует,что c(G)=3.
2.Рассмотрим рёберную раскраску. Из Теорем 2.8, 2.9 следует, что max d(v) £ c¢(G) £ m. В данном примере: 4£ c¢(G)£ 7.Так как правильную рёберную раскраску графа можно построить четырьмя цветами (на рисунке цвета рёбер обозначены I*,II*,III*,IV*), то отсюда следует: c¢(G)=4.
Ответ: c(G) =3, c¢(G) = 4. Правильные вершинная и рёберная раскраски графа даны на рис.2.11.
В ряде случаев построение правильных рёберных раскрасок проще производить с использованием матрицы смежности графа. В ней ребра вместо единиц отмечаются числовыми обозначениями присвоенных им цветов. Например, для графа на рис.2.11 соответствующая матрица смежности имеет вид:
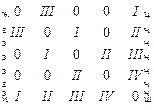
Матрица смежности, соответствующая правильной реберной раскраске, обладает следующим свойством — в каждой строке и каждом столбце не может больше одного раза встречаться обозначение одного и того же цвета.
Точные значения хроматических чисел получены для отдельных классов графов, например, для планарных графов (допускающих укладку на плоскости без пересечения ребер), графов, не содержащих нечетных простых циклов.
Теорема 2.10. Д.Кенига c(G) =2 тогда и только тогда, когда граф G не содержит нечетных простых циклов.
Теорема Кенига позволяет упростить определение хроматического числа некоторых видов графов.
В общем случае для определения точных значений хроматических чисел графов и построения их правильных раскрасок используют комбинаторные алгоритмы, основанные на переборе вариантов.
2.4. Планарность графов
В некоторых прикладных задачах требуется расположить граф на двумерной поверхности (плоскость, шар, многогранник, тор и др.) таким образом, чтобы рёбра графа не пересекали друг друга.
Определение. Планарным называют граф, который может быть изображён на плоскости так, чтобы его рёбра не пересекались. Геометрическое изображение планарного графа, при котором его рёбра не пересекаются, называют плоским графом.
Пример 1. Рассмотрим примеры планарных графов и их плоские изображения:
Рис.2.12. Примеры планарных графов и их плоские изображения
Каждый планарный граф также может уложен без пересечения рёбер на сфере или других видах поверхностей. Критерием планарности графов является
Теорема 2.11. Понтрягина-Куратовского.
Граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных графам К 5 и К 3,3 .
Пример 2. Определить планарность графа К 4,4 .
Решение. Поскольку граф К 4,4 содержит в качестве подграфа К 3,3, то по теореме Понтрягина—Куратовского он не планарен.
Определение. Часть плоскости, ограниченную простым циклом плоского графа и не содержащую внутри себя других вершин и рёбер, называют его гранью. Цикл, ограничивающих грань, называют границей грани. Грани, находящиеся внутри плоского графа, называют внутренними, грань, находящаяся снаружи —внешней.
Каждое ребро плоского графа принадлежит ровно двум граням. Его удаление приводит к тому, что две грани сливаются в одну.
Для плоских графов (псевдографов) справедлива
Теорема 2.12. Формула Эйлера.
Если n — количество вершин, m — количество рёбер, r — количество граней некоторого связного плоского графа G, то
r + n – m = 2.
Замечание. Формула Эйлера может быть применена только к плоским графам, у которых можно выделить грани.
Пример 3. Проверить выполнимость формулы Эйлера дляплоского графа G = (V, X), V = (1, 2, 3, 4, 5, 6), X = ((1, 2), (1, 3), (1, 4), (2, 3), (3, 4), (4, 5), (4, 6), (5, 6)) на рис.2.13.
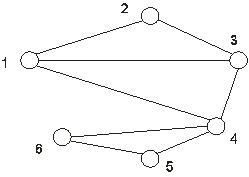
Рис.2.13
Решение. Характеристики графа следующие: n=6, m = 8, r=4(3 внутренних грани и одна внешняя). Подставляя в формулу Эйлера, получим: 4+6 - 8=2.
Пример 4. Доказать, что граф К5 не планарен.
Решение. Основные характеристики графа следующие: n=5, m = С25= (5×4)/(2×1) = 10. Если допустить планарность рассматриваемого графа, то должно существовать его плоское изображение. Из формулы Эйлера найдём число граней в плоском изображении: r = 2 – n + m = 2– 5 + 10 = 7. Так как каждая грань полного графа должна содержать не менее трёх ребер, то общее число рёбер в гранях (с учётом повторов при подсчёте) должно быть не меньше 21. Поскольку одно ребро в плоском графе может входить в состав ровно двух граней, то общее число рёбер должно быть не меньше 11. Однако, m = 10.Отсюда вытекает, что плоская укладка графа К5 не существует. Следовательно, он не планарен, что и требовалось доказать.
Дата добавления: 2015-10-05; просмотров: 5968;