Графовая организация данных

Рис.1. Этапы разработки компьютерной информационной модели

Способы структурирования информации

Графовая организация данных

Данные, используемые в любой информационной модели, всегда определенным образом упорядочены, структурированы. Иначе можно сказать так: данные, на которых базируется информационная модель, представляют собой систему со всеми характерными признаками – элементным составом, структурой, назначением. Такие структурированные системы данных часто называют структурами данных. Исследуя некоторую реальную систему (объект моделирования), системный аналитик строит ее теоретическую модель (см. рис.3.1). В первую очередь он должен описать структуру данных. Мы рассмотрим два основных способа, применяемых для описания структур данных: графы и таблицы.

Определение и свойства графа. Информация о некотором реальном объекте может быть представлена по-разному. В разговорной речи мы используем словесное (вербальное) представление информации. Вот, например, словесное описание некоторой местности: «Наш район состоит из пяти поселков: Дедкино, Бабкино, Репкино, Кошкино и Мышкино. Автомобильные дороги проложены между: Дедкино и Бабкино, Дедкино и Кошкино, Бабкино и Мышкино, Бабкино и Кошкино, Кошкино и Репкино». По такому описание довольно трудно представить себе эту местность, а, тем более, запомнить его. А представьте себе, что поселков не 5, а 25! Все гораздо понятнее становится из следующей схемы (на ней поселки обозначены первыми буквами своих названий):

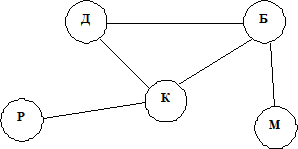
Рис.2. Неориентированный граф (сеть)

Это не карта местности. Здесь не выдержаны направления по сторонам света, не соблюден масштаб. На этой схеме отражен лишь факт существования пяти поселков и дорожной связи между ними. Такая схема называется графом.

Граф отображает элементный состав системы и структуру связей.Составными частями графа являются вершины и ребра. Здесь вершины изображены кружками – это элементы системы, а ребра изображены линиями – это связи (отношения) между элементами. Глядя на этот граф легко понять структуру дорожной системы в данной местности.

Построенный граф позволяет, например, ответить на вопрос: через какие поселки надо проехать, чтобы добраться из Репкино в Мышкино. Видно, что есть два возможных пути; обозначим их так:

1) Р – К – Б – М

2) Р – К – Д – Б – М

Очевидно, первый путь более выгодный, потому что он короче. Однако, если по какой-то причине дорога между К и Б окажется не проезжей (идут ремонтные работы или занесло снегом), то единственным остается второй путь. Граф на рис.3.4 еще называют сетью.

Для сети характерна возможность множества различных путей перемещения по ребрам между некоторыми парами вершин.

Для сетей также характерно наличие замкнутых путей, которые называются циклами. На рис.2 имеется цикл: К – Д – Б – К. Кстати, термин «дорожная сеть» используется и в разговорной речи. И чем такая сеть гуще, тем лучше для сообщения, поскольку появляется множество различных вариантов проезда.

Граф, изображенный на рис.2, является неориентированным графом. На нем каждое ребро обозначает наличие дорожной связи между двумя пунктами. Но дорожная связь действует одинаково в обе стороны: если по дороге можно проехать от Б к М, то по ней же можно проехать и от М к Б. Такую связь еще называют симметричной.

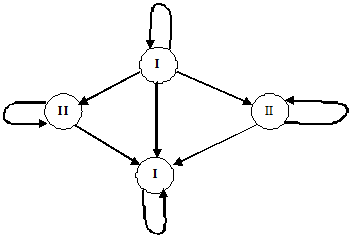
Рис.3. Ориентированный граф

Рассмотрим другой пример графа, изображенного на рис.3. Этот пример относится к медицине. Известно, что у разных людей кровь отличается по группе. Существуют четыре группы крови. Оказывается, что при переливании крови от одного человека к другому не все группы совместимы. Граф на рис.3 показывает возможные варианты переливания крови. Группы крови – это вершины графа с соответствующими номерами, а стрелки указывают на возможность переливания одной группы крови человеку с другой группой крови. Например, из этого графа видно, что кровь 1-й группы можно переливать любому человеку, а человек с первой группой крови воспринимает только кровь своей группы. Видно также, что человеку с 4-й группой крови можно переливать любую, но его собственную кровь можно переливать только в ту же группу.

Связи между вершинами данного графа несимметричны и поэтому изображаются направленными линиями со стрелками. Такие линии принято называть дугами (в отличие от ребер неориентированных графов). Граф с такими свойствами называется ориентированным. Линия, выходящая и входящая в одну и ту же вершину, называется петлей. На рис.3 присутствуют четыре таких петли.

Нетрудно понять преимущества изображения системы переливания крови в виде графа по сравнению с вербальным (т.е. словесным) описанием тех же самых правил. Граф на рис.3 легко воспринимается и запоминается.

Одним из классов ориентированных графов являются блок-схемы алгоритмов. В блок-схемах используются вершины разных типов, обозначающие разные команды: прямоугольник – команда присваивания; ромб – команда выбора пути продолжения алгоритма по результату проверки условия; параллелограмм – команда ввода или команда вывода; овал – начало или конец исполнения алгоритма. Здесь тоже можно говорить о пути прохождения графа в ходе выполнения алгоритма. Любой путь начинается от вершины начала и заканчивается выходом на вершину конца. Внутри же путь может быть разным в зависимости от исходных данных.

Иерархические структуры и деревья.При построении информационных моделей многих систем приходится иметь дело с иерархической структурой. Как правило, иерархическую структуру имеют системы административного управления, между элементами которых установлены отношения подчиненности. Например: директор завода – начальники цехов – начальники участков – бригадиры – рабочие. Иерархическую структуру имеют также системы, между элементами которых существуют отношения вхождения одних в другие. Например: федерация – республики – области – города – районы.

На рис.4 изображен «географический» граф, отражающий иерархическую структуру нашей планеты: Земля – материки – страны – регионы – города. Такой граф называется деревом. Основным свойством дерева является то, что между любыми двумя его вершинами существует единственный путь. Деревья не содержат циклов и петель.

Рис.4. Граф иерархической системы («географическое дерево»)

Обычно у дерева, отображающего иерархическую систему, выделяется одна главная вершина, которая называется корнем дерева. Эта вершина изображается вверху; от нее идут ветви дерева. От корня начинается отсчет уровней дерева. Вершины, непосредственно связанные с корнем, образуют первый уровень. От них идут связи к вершинам второго уровня и т.д. Каждая вершина дерева (кроме корня) имеет одну исходную вершину на предыдущем уровне и может иметь множество порожденных вершин на следующем уровне. Такой принцип связи называется «один ко многим». Вершины, которые не имеют порожденных, называются листьями. На рис.4 вершины, обозначающие города, являются листьями.

В качестве примера организационной системы с иерархической структурой рассмотрим университет. В его состав входит несколько факультетов: механико-математический, физический, исторический, юридический, экономический и другие. На каждом факультете студентов обучают по нескольким направлениям и специальностям. Например, на механико-математическом факультете существуют направления математика, прикладная математика, механика. В свою очередь, по каждому направлению учится много студентов. Вся эта система: университет – факультеты – специальности – студенты имеет иерархическую структуру. Вот фрагмент дерева, изображающего эту иерархию:

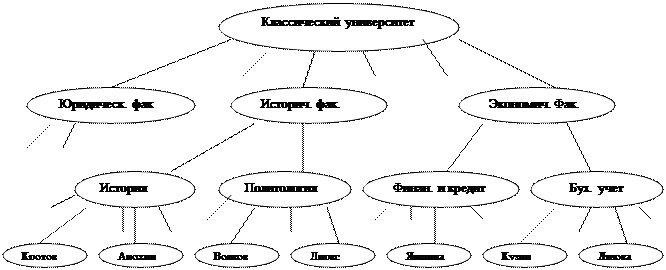
Рис.5. Иерархическая структура университета

Иерархическими являются различные системы классификации в науке. Например, в биологии весь животный мир Земли рассматривается как система, которая делится на типы животных, типы делятся на классы, классы состоят из отрядов, отряды – из семейств, семейства делятся на роды, роды – на виды. Следовательно, система животных имеет шестиуровневую иерархическую структуру.

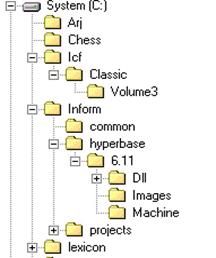
Рис.6. Иерархическая структура каталогов и файлов

Другой пример – система хранения файлов на магнитных дисках. Корнем этого дерева является корневой каталог диска, вершины – подкаталоги разных уровней. Как известно, путь к файлу – это путь от корневого каталога до каталога, непосредственно содержащего данный файл. И для каждого файла такой путь единственный. Например, путь к файлам, содержащимся в каталоге Images на рис.6, описывается так:

\Inform\hyperbase\6.11\Images

При поиске информации в дереве перемещение по нему может происходить только вверх или вниз (на уровень выше или на уровень ниже). Нельзя осуществить прямой переход между вершинами одного уровня.

Еще одним примером иерархической структуры является система доменных адресов в Интернете. Вот фрагмент этой системы, представленный в виде дерева.

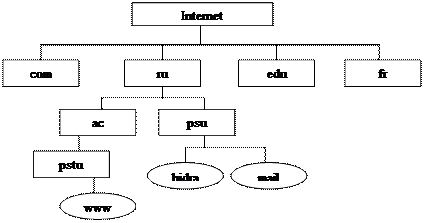
Рис.7. Иерархическая структура доменных адресов в Internet

В этом дереве от корня отходят домены первого уровня, затем второго и т.д. Овалами изображены компьютеры. Адрес компьютера (читается справа налево) включает в себя последовательность доменов, начиная с первого уровня, и кончая именем компьютера. Для трех указанных на рис.3.10 компьютеров доменные адреса записываются так:

www.pstu.ac.ru hidra.psu.ru mail.psu.ru

Каждую вершину дерева, не являющуюся листом, можно рассматривать как корень поддерева, исходящего из этой вершины. Например, на рис.3.10 поддерево с корнем в вершине ru представляет структуру доменных имен российского сектора Internet.