Изоморфизм, гомоморфизм, аналогия.

В связи со сложностью больших систем необходимо при исследовании прибегать к некоторым упрощениям. Методологией упрощения систем и занимается общая теория моделирования. Всякое исследование системы начинается с построения ее модели. Используют понятия характеризующие соответствие между структурами объектов: изоморфизм, гомоморфизм и аналогия.

Изоморфизм(изоморфный- одинаковый по форме) –есть взаимооднозначное соответствие между двумя множествами М и М¹ элементов или объектов.

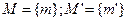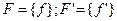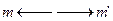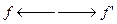Пример: даны множества и множества отношений . Если между элементами M и M’, а также отношениями F и F’ можно установить взаимооднозначные соотношения и , такие, что из выполнения соотношений f для M следует выполнение f’ для M’ и обратно то M и M’ изоморфны. При этом полный изоморфизм может быть лишь между геометрической фигурой и ее аналитическим выражением в виде формулы (например – круг и S =П _* R²). Учитывая, что изоморфизм связан не со всеми, а лишь фиксированными нами свойствами, можно за счет выбора структурных элементов получить близкие к изоморфным отношения и для реальных объектов.

Гомоморфизм (гомоморфный- подобный по форме) – есть не взаимооднозначное соответствие между двумя множествами элементов- один элемент множества М может соответствовать многим элементам множества М¹ (примеры: карта – местность; материальная точка – небесное тело и т.д.)

Аналогия – усть установление сходства в некоторых сторонах, качествах и отношениях между нетождественными объектами. Если объект А обладает признаками a, b, c, d; объект B обладает признаками a, b, c – возможно объект B обладает признаком d.

Аналогия не является строгим доказательством сходства объекта (системы) и для полного доказательства необходимы другие методы.