Критерии подобия

Пусть х_1А, х_2А, …, х_nА- переменные, значения которых непрерывно изменяются в пределах системы А, а х_1В, х_2В, …, х_nВ — те же переменные для системы В. Заметим, что переменные х_iА или х_jB являются размерными.

Известно, что никакие реальные закономерности, существующие в природе, не могут зависеть от выбора системы единиц измерения. Поэтому всякая реальная закономерность может быть предста­влена в виде зависимости между безразмерными величинами- критериями подобия.

При установлении подобия систем рассматриваются критерии подобия:

П_1А, П_2А, ..., П_kA - в системе А;

П_1B, П_2B, ..., П_kB - в системе В.

Различают два вида критериев подобия - симплексы и ком­плексы:

· Симплекс - отношение двух каких-либо параметров одной и той же физической природы. Например, отно­шение двух линейных размеров (длины к диаметру) - L/D. Или, при моделировании двухфазной системы (шлак- металл) примером критерия- симплекса может служить отношение поверхностного натяжения шлака, к поверхностному натяжению металла- S_шл / S_ме

· Комплекс - отношение более чем двух параметров. Примеры - комплексов:

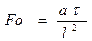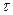1. Критерий Фурье , где - некоторое время, характеризующее скорость изменения внешней обстановки, с; а- коэффициент температуропроводности, м²/с; l - характерный размер, заданный по условию, м (для плиты l равно половине ее толщины, для цилиндра — его радиусу). Число Фурье имеет смысл обобщенного времени.

2. Критерий Био 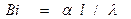где 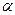- коэффициент теплообмена (теплоотдачи), Вт/(м²_*К); l - характерный линейный размер, м; 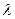- коэффициент теплопроводности, Вт/(м_*K). Физический смысл критерия Bi состоит в том, что его можно считать показателем массивности тела. Если Bi <= 0,25, то тело можно считать тонким; при Bi >= 0,50 тело является массивным; если 0,25 < Bi < 0,50- считают, что тело находится в переходной области.

3. Критерий Рейнольдса Re = w * l / v, где w - скорость потока, м/с; l - характерный размер, м; v- кинематическая вязкость, м²/с. Критерий Рейнольдса рассматривают как показатель ре­жима течения жидкости или газа. Если рассма­тривать относительное движение частички, диаметр которой ра­вен l, в жидкости или газе, то при Re <, 2 режим течения можно считать ламинарным, при Re = 2 - 500 - переходным и при Re > > 500 - турбулентным.

Пусть Z _j (x₁, х₂, . . ., х_n) — закономерность, интересующая исследователя. От Z _j перейдем к безразмерной величине Z^*_j = Z _j / Z₀ (здесь Z₀ - масштаб модели). Каким-то способом установим зависимость

Z^*_j = f (П₁, П₂, ..., П_k) (3.5)

Случаи подобия систем:

· Согласно физической теории подобия система В будет по­добна системе А в том случае, когда будут одинаковы значения Z^*_j у двух систем при одинаковых критериях подобия П₁, П₂, ..., П_k. Равенство критерия подобия для модели и исходной системы обозначают знаком idem «одно - и то же». Например, если выполняется соотношение F₀ = idem , то протекание процесса в системе В гомохронно его протеканию в системе А. Если же для систем В и A величина а/l² имеет одно и то же значение, то для них, очевидно, гомохронность переходит в синхронность.

· В случае, когда не осуществляется переход к безразмерным критериям подобия, подобие двух систем определяется следующим образом - системы A и B называют подобными, если в любые сходственные моменты вре­мени значения соответствующих выходных переменных, для этих систем пропорциональны друг другу. Очевидно, что при этом значения соответствующих входных переменных x_i не обязаны совпадать.

Требования теории физического подобия об аналогии между моделью и образцом:

1) модель должна быть геометрически подобна образцу;

2) явления в модели и образце должны принадлежать к одному и тому же классу, т. е. описываться одной системой диф­ференциальных уравнений;

3) начальные и краевые условия в модели должны быть реали­зованы таким образом, чтобы безразмерные начальные и краевые условия модели тождественно совпадали с такими же условиями образца;

4) одноименные безразмерные параметры (критерии подобия), входящие в систему дифференциальных уравнений, описывающую моделируемые явления, в модели и в образце должны быть соответ­ственно равны.