Моделирование процессов при воздействии случайных факторов.

В реальных системах часто имеют дело со случайными вели­чинами. Один и тот же технологический процесс может протекать по различным схемам (чугун в сталеплавильный агре­гат могут подавать либо из миксера, либо непосредственно из доменного цеха; в одних случаях требуется остановка агрегата на мелкий ремонт, а в других нет; иногда разливка плавки произ­водится на одной площадке, иногда на другой). Химический состав сырья подвержен случайным колебаниям, задержки периодов плавки, сортность продукции представляют собой типич­ный пример случайных величин.

Метод Монте-Карло. Для моделирования систем, характеризующихся дей­ствием большого числа случайных факторов, приспособлен метод статистических испытаний (Монте-Карло). Вместо того чтобы наблюдать за поведением реальной системы и собирать статисти­ческий материал, с помощью которого можно оценить характеристики системы (например, производи­тельность, простои, расходы ресурсов и др.), при использовании статистических испытаний регистрируют значения соответствую­щих характеристик модели, а затем подвергают их статистической обработке.

При моделировании случайные числа получаются с помощью «розыгрыша» - на основании «жребия». Метод Монте-Карло может быть реализован либо вручную, либо с помощью ЭВМ.

В первом случае для получения чисел исполь­зуются, например, специальные таблицы, устройства типа игор­ной рулетки, лотерейного барабана и др. Во втором случае при­бегают к использованию физических датчиков случайных чисел, основанных на преобразовании случайных сигналов, а также к использованию различных машинных алгоритмов (генераторов), обеспечи­вающих получение так называемых псевдослучайных чисел.

В стохастической модели существуют два типа случайных величин:

· Величины первого типа воспроизводятся по известным заранее распределениям, характерным для реального объекта. Например, при моделировании работы цеха, в мо­дели разыгрывается начальная ситуация на входах цеха (плано­вое задание, поступление ресурсов, обеспеченность оборудова­нием и др.) и колебания в условиях работы (спо­собы проведения процесса).

· Случайные вели­чины второго типа - это величины, получаемые на выходах модели. Они выявляются в процессе моделирования (длитель­ности задержек, производительности агрегатов и др.).

При моделировании методом Монте-Карло приходится иметь дело с двумя классами задач: первый связан с необходимостью ввода в модель конкретных слу­чайных величин первого типа; второй связан с оценкой характеристик случайных величин второго типа (математического ожидания, дисперсии и др.).

Пример использования метода Монте-Карло в детерминированных системах. Детерминиро­ванную задачу сведем к вычислению вероятности попадания точки в фигуру. (Задачу можно переформу­лировать и сказать, что она сводится к определению вероятности поражения какой-либо цели). Речь идет о вычислении определенного интеграла методом Мон­те-Карло. Вычислим интеграл:

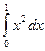; очевидно, он равен 1/3 (4.1)

Рассмотрим квадрат, вершины которого имеют коор­динаты (0,0); (0,1); (1,1); (1,0). Проведем в нем кривую y = х². Будем осуществлять статистические испытания, из таблицы [27] равномерно распре­деленных на отрезке (0,1) случайных чисел выписываем N пар чисел, выполняя при этом проверку условия у <= x². Возьмем, например, N= 20. Тогда окажется, что из рассмотренных 20 точек 7 точек (m = 7) будут лежать под параболой или на ней.

Согласно геометрическому определению вероятности, вероятность попада­ния точки в фигуру пропорциональна площади этой фигуры. Поэтому искомая площадь треугольника S _тр будет относиться к площади квадрата S_кв, как S_тр / S_кв = m / N.Но S_кв ~=1 и, следовательно, S_тр ~= m / N. Для рассматриваемого примера S_тр ~ = 7 / 20 = 0,35. В данном случае аналитический метод проще. Если статистические испытания использовать для вычисления «неберущихся» интегралов, то преимущество метода Монте-Карло становится очевидным.

Контрольные вопросы:

1. Основные этапы построения моделей.

2. Сущность воспроизведения протекания технологического процесса.

3. Содержание метода Монте-Карло и практика его реализации.

Характеристика детерминированных и статистических моделей.