Теория подобия систем.

В моделировании процессов широко применяется теория подобия, которая занимается определением степени соответствия между моделью и объектом на основе критериев (чисел) подобия и в значительной мере играет роль методологической базы моделирования.

Основными понятиями теории подобия являются:

·Параметры процесса – переменные, характеризующие изменение состояния процесса во времени или пространстве;

·Параметры системы - переменные, характеризующие изменение элементов системы во времени или пространстве.

Считается, что процессы (явления) подобны друг другу, если существует некоторое соответствие сходственных величин изучаемых систем: Положение точек, геометрических размеров (т.е. параметров систем и процессов) и т.д.

На практике имеют дело с приближенным, а не абсолютным подобием- системы считают подобными если подобны наиболее существенные процессы (для данной задачи).

Теория подобия базируется на трех теоремах:

1. Первая теорема. Явления, подобные в том или ином смысле (физически, математически, кибернетически и т.д.) имеют некоторые одинаковые сочетания параметров, называемые критериями (числами) подобия. – У всех подобных процессов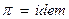

Пример: Изучаются процессы, описываемые уравнениями члены которых являются однородными функциями параметров или их производных.

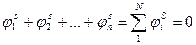(3.1)

где S = 1,2,…,k – количество подобных процессов (уравнений);

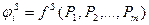- функции параметров или производных.

Приведя уравнения к безразмерному виду делением на n- член и учитывая тождество уравнений, получаем математическую формулировку 1-й теоремы

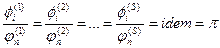(3.2)

2. Вторая теорема-( 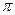-теорема). Всякое полное уравнение физического процесса, записанное в определенной системе едениц (СИ, СГС и др.) может быть представлено зависимостями между критериями подобия (уравнением связывающим безразмерные величины полученные из участвующих в процессе параметров).

Примечание: 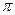-теорема относится только к процессам отражаемым полными уравнениями.

Пример: Связи между параметрами процесса и параметрами элементов системы можно записать в виде 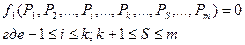(3.3)

Эта зависимость называется полной, если она учитывает все связи и в соответствии с 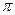-теоремой можно перейти к зависимости между критериями

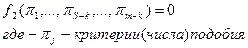(3.4)

Уравнение дает связь между m-k критериев вместо m-исходных параметров.

3. Третья теорема. (Необходимые и достаточные условия). Для подобия явлений должны быть соответственно одинаковыми определяющие критерии подобия (содержащие независимые параметры процессов и систем) и подобны условия однозначности (параметры и зависимости, выделяющие данное явление из многообразия явлений данного вида).

Теория подобия использует дополнительно два положения:

1.Положение-1 - Подобие сложных систем 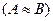, состоящих из нескольких подсистем подобных в отдельности 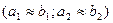, обеспечивается подобием всех сходственных элементов, являющихся общими для подсистем.

2.Положение-2- Все теоремы, относящиеся к детерминировано заданным системам справедливы для случаев с вероятностным характером явлений при условиях:

· Должны быть одинаковыми плотности вероятностей для сходственных параметров (представленных в виде относительных характеристик), а также математические ожидания и дисперсии (с учетом масштабов);

· Должна быть физическая реализуемость сходственной корелляции между стохастически заданными параметрами, входящими в условия однозначности.