Дробные и смешанные числа в позиционных системах счисления с постоянными основаниями

В позиционных системах счисления вещественные числа представляют при помощи целой и дробной частей, разделенных между собой запятой. И целую часть и дробную записывают при помощи последовательности отдельных знаков, стоящих в разрядах – местах, за которыми закреплен порядковый номер, отсчитываемый от запятой. В целой части отсчет идет от разделяющей запятой справа – налево от 0 и выше. Дробная часть изображается в разрядах, стоящих слева – направо. Номера разрядов в ней убывают от (–1) слева – направо. При этом дробные числа в системах с постоянным основанием р разлагают при переводах по отрицательным (–1, –2, …)степеням р. Таким образом, запись А_p=0,a_–1a_–2 …a_–s в развернутой форме означает: А_p = a_–1p^–1+a_–2p^–2+…+a_–s p^–s.

Пример 1. 0,47₁₀ = 4×10^–1 + 7×10^–2; 0,265₇ = 2×7^–1 + 6×7^–2 + 5×7^–3.

Правильная дробь имеет нулевую целую часть. Результат перевода правильной дроби – всегда правильная дробь. Обыкновенной дробью называется ее представление в виде отношения целых чисел ±m/n, где m (числитель) – целое число, а n (знаменатель) – натуральное число.

Обыкновенные дроби также называют рациональными. Дроби, не представимые в виде отношения целых чисел ±m/n, называют иррациональными.

В позиционной системе счисления с основанием p правильная дробь имеет вид (0,a_–1a_–2 …a_–s), представляющий разложение числа по отрицательным (–1, –2, …) степеням p. Все величины, стоящие в разрядах дроби в системе с основанием p, как и у целых чисел, могут принимать значения от 0 до (p – 1).

Дроби, задающие рациональные числа, могут быть конечными и бесконечными (периодическими). У конечной дроби запись обрывается, например 0,247₈. Бесконечная дробь помимо постоянной части (предпериода) имеет периодическую, которая теоретически повторяется в записи бесконечное число раз. Данную часть записи дроби называют периодом. В точной записи дроби данную часть записи приводят один раз в круглых скобках.

Пример 2.Бесконечная шестнадцатеричная дробь 0,В7С(2А)₁₆имеет предпериод В7С и период, равный 2А. Значение дроби можно представить бесконечной записью вида 0,В7С2А2А2А2А2А…₁₆ =0,В7С(2А)₁₆.

Замечание. Конечные дроби могут быть представлены частным случаем бесконечных, у которых период равен нулю – (0).

Смешанным называют число со знаком, в котором явно выделены ненулевые целая и дробная части. Смешанные числа в зависимости от способа представления дробной части можно представлять в виде записи с обыкновенной дробью либо записи в позиционной систем счисления.

Пример 3.Смешанное число, приближающее число p:

.

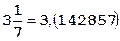Переводы смешанных чисел сводятся к отдельному переводу их целых и обыкновенных дробных частей.

4.3.1 Перевод правильных десятичных дробей в систему счисления с иным основанием p ¹ 10

В десятичной системе счисления (p = 10) дроби разлагаются по степеням числа 1/10, а в системах с основаниями вида p ¹ 10 – по степеням чисел 1/p. При переходе от десятичной дроби к дроби по иному основанию p коэффициенты нового разложения можно найти, последовательно умножая исходную дробь на новое основание p и отделяя получаемую при этом целую часть. Если процесс обрывается (в дробной части получен 0), то получаемая дробь – конечная; если продолжается (дробная часть ненулевая), то вычисления производят до тех пор, пока не будет получена искомая точность (число знаков после запятой) либо не найден период дроби.

Обычно, если число знаков искомой дроби не оговаривается, в условии задачи имеется в виду поиск ее точного выражения – конечного или в периодическом виде.

Пример 4.Перевести в двоичную систему счисления дробь 0,75₁₀.

Решение.

0,75 0,5

´ 2 ´ 2

1,50 1,0.

В дробной части получен 0, следовательно, искомая двоичная дробь конечная.

Ответ: 0,75₁₀ =0,11₂.

Пример 5.Перевести в двоичную систему счисления дробь 0,8₁₀.

Решение.

0,8 0,6 0,2 0,4 0,8

´ 2 ´ 2 ´ 2 ´ 2

1,6 1,2 0,4 0,8.

Процесс остановлен, так как найден полный период бесконечной дроби (значение 0,8 получено вновь). Следовательно, искомая двоичная дробь – бесконечная (периодическая). Постоянная часть дроби отсутствует, период равен 1100₂.

Ответ: 0,8₁₀ =0,(1100)₂.

Пример 6.Перевести в шестнадцатеричную систему счисления дробь 0,22265625₁₀.

Решение.

0,22265625 0,5625

´ 16 ´ 16

3,56250000 9,0000.

В дробной части получен 0, следовательно, искомая шестнадцатеричная дробь – конечная.

Ответ: 0,22265625₁₀ =0,39₁₆.

Пример 7.Перевести в восьмеричную систему счисления дробь 0,65₁₀. Найти полное выражение.

Решение.

0,65 0,2 0,6 0,8 0,4 0,2

´ 8 ´ 8 ´ 8 ´ 8 ´ 8

5,20 1,6 4,8 6,4 3,2

Дробь 0,2 получена повторно, поэтому процесс деления остановлен, так как найден полный период бесконечной дроби – 1463. Постоянная часть дроби – последовательность цифр перед периодом, равная 5.

Ответ: 0,65₁₀ =0,5(1463)₈.

Пример 8.Перевести в систему счисления с основанием 4 дробь 0,035₁₀. Результат определить с точностью до 6 знаков после запятой.

Решение.

0,035 0,14 0,56 0,24 0,96 0,84

´ 4 ´ 4 ´ 4 ´ 4 ´ 4 ´ 4

0,140 0,56 2,24 0,96 3,84 3,36

Искомые 6 знаков получены, процесс перевода остановлен.

Ответ: 0,035₁₀ »0,002033₄.

4.3.2 Перевод правильных дробей из системы с основанием p ¹ 10
в десятичную систему счисления

Единица разряда с номером (–k) у дроби в системе счисления с основанием p = 2^s в десятичной системе счисления равна десятичному числу (2)^–ks = (0,5)^ks. Поэтому перевод дроби, имеющей запись A_p = 0,a_–1 ...a_–k в системе счисления с основанием p = 2^s, в десятичную систему счисления производят по формуле:

A₁₀ = a_–1(0,5)^s + ... + a_–k(0,5)^ks.

Пример 9.Перевести в десятичную систему счисления восьмеричную дробь 0,26₈.

Решение. С учетом того, что 8=2³, s = 3 получим:

А₁₀ =2× (0,5)³ +6× (0,5)⁶ =2×0,125+6×0,015625 = 0,25+0,09375=0,34375₁₀.

Ответ: 0,26₈ =0,34375₁₀.

Если основание p не равно степени 2, то перевод дроби в десятичную систему проще осуществлять по следующему общему правилу. Вначале дробную часть представляют в виде единой обыкновенной дроби m/n. Выполняя деление m на n в десятичной системе (любым способом), получаем искомую десятичную дробь. Если она конечна, то найдено точное решение задачи.

Если полученная дробь бесконечная и задана точность, с которой она должна быть определена (число k знаков после запятой), то оставляем (k + 1) знак в записи дроби, округляем ее, отбрасываем последний знак и получаем искомый ответ.

Если для бесконечной десятичной дроби требуется найти точное выражение, то по ее записи вначале определяют предпериод (постоянную часть после запятой) и период (повторяющуюся часть после предпериода). Точная запись дроби состоит из предпериода и периода, взятого в круглые скобки.

Пример 10.Найти с точностью до 6 знаков после запятой приближенное значение в десятичной системе счисления семеричной (p = 7) дроби 0,165₇.

Решение. Вначале переводим заданную дробь в обыкновенную форму:

0,165₇ =1×(1/7) +6×(1/7)² +5×(1/7)³ =96/343.

Выполняя деление до седьмого знака после запятой, получим:

96/343=0,2798833… .

Округляя последний знак, получим искомую приближенную десятичную дробь:

0,2798833»0,279883.

Ответ: c точностью до 6 знаков после запятой 0,165₇ »0,279883₁₀.

Пример 11.Для шестеричной (p = 6) дроби 0,31₆ найти в десятичной системе счисления:

1) точное выражение,

2) приближенное значение с точностью до 5 знаков после запятой.

Решение. Вначале переводим заданную дробь в обыкновенную форму:

0,31₆ =3×(1/6) +1×(1/6)² =19/36.

Выполняя деление, выделяя предпериод и период, получим искомое точное выражение 1) в периодической форме:

19/36=0,52777777… =0,52(7).

Приближенное выражение 2) получим, округляя полученную бесконечную дробь до 5 знака после запятой: 0,52777777… »0,52778.

Ответ: 1) 0,52(7)₁₀,2)0,52778₁₀.

4.3.3 Перевод правильных дробей из системы счисления
с основанием p = 2^s в двоичную систему счисления

Рассмотрим также “быстрые” правила перевода дробей. Для осуществления данного перевода из основания p = 2^s в двоичную систему все величины, стоящие в разрядах дроби, заменяют их двоичными записями длины s (со всеми незначащими нулями). Если исходная дробь является периодической, то длина ее периода в двоичной системе счисления может сократиться. Незначащие нули справа в итоговом двоичном представлении можно убрать.

Пример 12.Перевести в двоичную систему счисления правильную конечную дробь, представленную в восьмеричной системе счисления: 0,3076₈.

Решение. 8=2³, s = 3. Представляя по очереди цифры дроби их двоичными записями длины s = 3, получим: 3₈ =011₂,0₈ =000₂,7₈ =111₂,6₈ =110₂.

Соединяя полученные двоичные выражения и отбрасывая незначащий нуль справа, получим искомое выражение.

Ответ: 0,3076₈ =0,01100011111₂.

Пример 13.Перевести в двоичную систему счисления правильную периодическую дробь, представленную в шестнадцатеричной системе счисления:0,В58(А)₁₆.

Решение. 16=2⁴, s =4. Представляя по очереди цифры постоянной части и периода дроби их двоичными записями длины s = 4, получим:

В₁₆ =1011₂,5₁₆ =0101₂,8₁₆ =1000₂,А₁₆ =1010₂.

Соединяя полученные двоичные записи, с учетом того, что период в двоичной системе счисления распадается на две одинаковые части, получим: 0,101101011000(10)₂

Ответ: 0,В58(А)₁₆ =0,101101011000(10)₂.

4.3.4 Перевод правильных дробей из двоичной системы счисления
в систему с основанием p = 2^s

Перевод производится следующим образом. Начиная со старших разрядов двоичной записи (после запятой), все цифры дроби группируются по s и заменяются цифрами в системе счисления с основанием p = 2^s. Если исходная двоичная дробь является конечной и в последней группе меньше, чем s знаков, ее справа дополняют незначащими нулями до s цифр. Если исходная двоичная дробь является периодической, ее период повторяется до тех пор, пока не определится период в новой системе счисления.

Пример 14.Перевести в четверичную систему счисления правильную конечную двоичную дробь 0,110110011₂.

Решение. 4=2²,s=2. Разбивая дробную часть слева направо по два знака и дополняя в последней группе единицу справа незначащим нулем, переводим полученные в группах двузначные двоичные числа в четверичную систему счисления:

11₂ =3₄,01₂ =1₄,10₂ =2₄,01₂ =1₄,10₂ =2₄.

Записывая слитно полученные цифры дроби, получим: 0,31212₄.

Ответ: 0,110110011₂ =0,31212₄.

Пример 15.Перевести в шестнадцатеричную систему счисления правильную периодическую двоичную дробь 0,110110(011)₂.

Решение. 16=2⁴, s =4.

Разбиваем дробную часть слева направо на группы по 4 знака и переводим двоичные числа в шестнадцатеричную систему счисления. Начиная со второй группы, в них входят цифры из периодов. Их выделим курсивом, начало и конец каждого периода дополнительно показаны скобками. Разбиение на группы и перевод чисел продолжаем до тех пор, пока не получим период в шестнадцатеричной системе счисления, который начинается с группы цифр, образованных периодом двоичного числа:

1101₂ =D₁₆;10(01₂ =9₁₆;1)(011)₂ =В₁₆; (011)(0₂ =6₁₆;11)(01₂ =D₁₆;1)(011)₂ =В₁₆.

Период шестнадцатеричной дроби равен (В6D) Записывая слитно полученные цифры основной части дроби и периодическую часть, получим: 0,D9(В6D)₁₆.

Ответ: 0,110110(011)₂ =0,D9(В6D)₁₆.

4.3.5 Перевод правильных дробей из системы счисления
с основанием p = 2^s в систему с другим основанием, равным степени 2

В общем случае перевод проще производить через двоичную систему счисления. При переводе из шестнадцатеричной системы счисления в четверичную можно использовать связь 4² =16 и переводить непосредственно пары цифр четверичной записи, отсчитываемые от запятой, в шестнадцатеричные цифры и обратно. В случае периодической дроби период исходной дроби переводится до тех пор, пока не будет найден период искомой дроби.

Пример 16.Перевести в восьмеричную систему счисления правильную периодическую шестнадцатеричную дробь 0,8А9(5Е)₁₆.

Решение. Сначала, используя правило 4.3.3, переводим шестнадцатеричную дробь 0,8А9(5Е)₁₆ в двоичную систему счисления:

8₁₆ =000₂;А₁₆ =1010₂;9₁₆ =1001₂;5₁₆ =0101₂;Е₁₆ =1110₂;

0,8А9(5Е)₁₆ =0,100010101001(01011110)₂.

Затем по правилу 4.3.4 переводим полученную двоичную дробь в восьмеричную систему счисления (курсивом выделены цифры, которые взяты из периода, начало и конец каждого периода показаны скобками):

100₂ =4₈;010₂ =2₈;101₂ =5₈;001₂ =1₈; (010₂ =2₈;111₂ =7₈;10)(0₂ =4₈;101₂ =5₈;111₂ =7₈;0)(01₂ =1₈;011₂ =3₈;110)₂ =6₈; (010₂ =2₈.

Период восьмеричной дроби найден и равен (27457136). Записывая слитно полученные цифры основной части дроби и периодическую часть, получим: 0,4251(27457136)₈.

Ответ: 0,8А9(5Е)₁₆ =0,4251(27457136)₈.

Пример 17.Перевести в шестнадцатеричную систему счисления из четверичной правильную периодическую дробь 0,2031223(21303)₄.

Решение. По упрощенному способу перевода из системы счисления с основанием p = 4 в шестнадцатеричную систему счисления (правило 4.3.5) сначала переводим пары цифр постоянной части дроби, отсчитывая их от запятой, затем переводим цифры из периода столько раз, чтобы определить период в искомой шестнадцатеричной записи (курсивом выделены цифры, которые взяты из периода, начало и конец каждого периода показаны скобками):

20₄ =8₁₆;31₄ =D₁₆;22₄ =A₁₆;3(2₄ =E₁₆;13₄ =7₁₆;03)₄ =3₁₆; (21₄ =9₁₆;30₄ =C₁₆;3)(2₄ =E₁₆.

Период восьмеричной дроби найден и равен (E739C). Записывая слитно полученные цифры основной части дроби и периодическую часть, получим: 0,8DA(E739C)₁₆.

Ответ: 0,2031223(21303)₄ =0,8DA(E739C)₁₆.

Число, содержащее целую и дробную части, называют смешанным. Для его перевода из одной системы в другую отдельно переводят целую часть, отдельно – дробную.

Пример 18.Перевести в шестнадцатеричную систему счисления из десятичной смешанное число 7069,2089₁₀. Ответ дать с точностью до 5 знаков после запятой.

Решение. 1. Сначала по правилу 4.2.2 переводим целую часть числа из десятичной системы счисления в шестнадцатеричную путем последовательного деления десятичной записи на 16. При этом остатки от деления на каждом шаге и самое последнее частное образуют искомую шестнадцатеричную запись числа в обратном порядке.

7069 ½ 16

7056 ½ 441 ½ 16

13432 ½ 27 ½ 16

916 ½1

11

Переводя значения в разрядах в шестнадцатеричную систему счисления и записывая их в обратном порядке, получим: 7069₁₀ =1B9D₁₆.

2. Затем по правилу 2.2.1 переводим дробную часть десятичной записи в шестнадцатеричную систему счисления путем последовательного умножения исходной дроби на 16. Поскольку необходимо найти 6 знаков после запятой, умножение выполняем 6 раз.

0,2089 0,3424 0,4784 0,6544 0,4704 0,5264

´ 16 ´ 16 ´ 16 ´ 16 ´ 16 ´ 16

3,3424 5,4784 7,6544 10,4704 7,5264 8,4224

Переводя значения в разрядах в шестнадцатеричную систему счисления и выполняя округление, получим: 0,2089₁₀ »0,357А78₁₆ »0,357А8₁₆.

Объединяя целую и дробную части, получим: 1B9D,357А8₁₆.

Ответ: 7069,2089₁₀ »1B9D,357А8₁₆.

Вопросы для проверки знаний.

1. Какие дроби называют правильными?

2. Какие дроби называют обыкновенными?

3. Какие дроби называют рациональными, а какие ‑ иррациональными?

4. Что называют предпериодом записи рациональной дроби в позиционной системе счисления?

5. Что называют периодом дроби в позиционной системе счисления и как его выделяют в записи?

6. Чем отличаются записи рациональных дробей от записей иррациональных дробей в позиционных системах счисления?

7. Может ли иррациональная дробь иметь конечную запись?

8. Что называют смешанным числом?