Коэффициенты взаимозависимости для номинального уровня измерения. 4 страница
Тогда

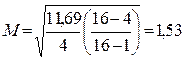
В зависимости от выбранной доверительной вероятности средняя заработная плата для генеральной совокупности 83,5 ±Z1,53. Например, исследователь может с вероятностью в 0,95 утверждать, что в данной генеральной совокупности средняя заработная плата не меньше 80,6 руб. и не больше 86,5 руб.
Так как вычисление ошибки для серийной выборки основано на дисперсии серийных средних, то серийный отбор будет тем репрезентативнее, чем меньше степень колеблемости серийных средних, измеряемая величиной их дисперсии.
4. Стратифицированный отбор
Понятие стратифицированной выборки. Вероятностная выборка с любой техникой отбора (простая случайная, систематическая, серийная или многоступенчатая) становится стратифицированной,
если процедурам отбора предшествует выделение в генеральной совокупности однородных частей, называемых стратами.
В статистическом смысле стратификация соответствует выделению таких статистически однородных групп, колеблемость изучаемых признаков которых внутри меньше, чем между ними.
Эта дифференциация внутри генеральной совокупности на качественно более однородные группы содержательно связана с предметом исследования.
Стратификация совокупности оказывается необходимой во всех случаях, когда совокупность является неоднородной по социальным, экономическим и другим характеристикам единиц наблюдения.
Так, исследуя профессиональную ориентацию школьников в пределах одного города, можно в одну страту отнести 16 школ, расположенных в районе старых застроек, во вторую — 20 школ, расположенных в районах новостроек. Для опроса можно отобрать выпускников из двух школ первой страты, а также из двух школ второй страты. Если такая группировка школ действительно отражает различия районов, которые существенно учитывать в исследовании профессиональной структуры, то колеблемость изучаемых признаков внутри каждой группы школ должна быть меньше, чем между группами.
В качестве страт могут быть использованы как естественные образования, так и специально формируемые для определенного исследования. Например, такими стратами могут выступать экономико-географические регионы или области страны, города, классифицированные по их административному статусу и по численности населения. Стратами могут выступать и идеальные образования. Примером является выделение в генеральной совокупности при исследовании отношения молодежи к труду, шести групп по содержанию труда[119].
Стратифицирующий признак. Признак, по значениям которого производится стратификация генеральной совокупности, называется признаком стратификации. Стратификация может проводиться по одному или нескольким признакам.
Организация стратифицированной выборки. Организация стратифицированной выборки требует представления о характере распределения по всей совокупности тех признаков, которые должны быть положены в основу образования типических групп, или страт.
Неправильный выбор признака для группировки элементов генеральной совокупности может не увеличить репрезентативность выборочных данных по сравнению со случайной выборкой того же объема.
Организация стратифицированной репрезентативной выборки связана на практике с известными трудностями, особенно если выделенные страты неравночисленны Математическая статистика рекомендует в этих случаях, чтобы размеры выборки из каждой страты были пропорциональны средним квадратическим отклонениям в соответствующих стратах генеральной совокупности. Но дисперсии, как правило, неизвестны. Поэтому часто при организации отбора из страт генеральной совокупности производится отбор пропорционально их размеру (доле) в общей численности совокупности.
Еще один употребляемый в социологии вариант выбора — это отбор одинакового количества единиц наблюдения из неравных типических групп.
Выборка организуется в зависимости от рассмотренных вариантов отбора с объемом, который рассчитывается по следующим формулам.
1. Пропорционально среднеквадратическому отклонению 5; в 1-й типической группе, найденному по результатам пробного исследования. Размер ( 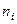 ) выборки из i-й типической группы равен
) выборки из i-й типической группы равен

где п — объем всей выборки;  — объем i-й группы в генеральной совокупности; l — количество групп. Весь объем выборки равен
— объем i-й группы в генеральной совокупности; l — количество групп. Весь объем выборки равен
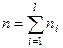
2. Пропорционально размеру групп:  , где N объем генеральной совокупности. Весь объем выборки равен
, где N объем генеральной совокупности. Весь объем выборки равен 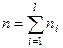 .
.
3. Отбор равного числа единиц наблюдения  . Весь объем выборки определяется по формуле
. Весь объем выборки определяется по формуле 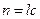 .
.
Расчет характеристик стратифицированной выборки. Характеристики такой выборки рассчитываются как взвешенные величины: показатели по каждой страте комбинируются в общую среднюю; вклад групповых средних пропорционален весу каждой страты в выборочной или генеральной совокупности.
В стратифицированной выборке общая дисперсия выборки имеет как бы два источника: дисперсию групповых средних, которые характеризуют каждую страту 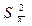 , и среднюю дисперсию из дисперсий внутри каждой из этих страт
, и среднюю дисперсию из дисперсий внутри каждой из этих страт 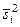 . Первую составляющую принято называть межгрупповой дисперсией, а вторую — внутригрупповой дисперсией.
. Первую составляющую принято называть межгрупповой дисперсией, а вторую — внутригрупповой дисперсией.
Это записывается следующим образом:
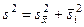 (7)
(7)
Расчет средней ошибки при отборе, пропорциональном численности единиц в стратах, производится по формуле
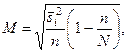 (8)
(8)
или, если пренебречь отношением n/N,
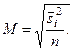 (9)
(9)
В выражениях (8) и (9) 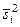 вычисляется исходя из формулы (7), т. е.
вычисляется исходя из формулы (7), т. е.  , где
, где 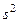 — общая дисперсия выборки — подсчитывается как для простой выборки, не принимая во внимание стратификацию.
— общая дисперсия выборки — подсчитывается как для простой выборки, не принимая во внимание стратификацию.
Таблица 19.Данные к примеру
| Семья | Группа (i) | ||||
| I | II | III | IV | V | |
| Размер на подписку, руб. | |||||
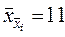
| 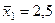
| 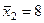
| 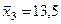
| 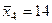
| 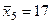
|
Из соотношения для средней ошибки (7) следует, что ошибка стратифицированной выборки меньше средней ошибки чисто случайной выборки либо равна ей, когда межгрупповая дисперсия равна нулю.
Пример. Предположим, что выборка содержит 5 страт (группы семей по среднему доходу[120]). Необходимо определить величину расходов на годовую подписку. Из каждой i-й страты взяты по две семьи (объем выборки п = 10, см. табл. 19),
Расчет:
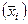
| 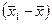
| 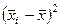
| 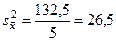
|
| 2,5 8,0 13,5 14,0 17,0 | —8,5 —3 2,5 3,0 6,0 | 72,25 9,00 6,25 9,00 36,00 | |
 = 11 = 11
| å = 132,5 |
Найдем дисперсию, не учитывая расслоение семей на 5 групп:
| № п/п | 
| 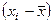
| 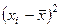
| 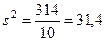
|
| —8 —9 —1 —5 | ||||
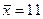
| å = 314 |
Отсюда внутригрупповая дисперсия 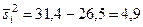 , ошибка для стратифицированной выборки
, ошибка для стратифицированной выборки  .
.
Для случайной выборки 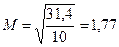 .
.
Таким образом, как видно из рассмотренного примера, стратифицированная выборка при прочих равных условиях дает более точные результаты.
5. Многоступенчатые и комбинированные способы формирования выборочной совокупности
Выборка может строиться как одно- или многоступенчатая.
При многоступенчатом отборе на каждой ступени меняется единица отбора. Например, на первой ступени производится отбор промышленных предприятий, на второй — отбор бригад на предприятиях, попавших в выборку па первой ступени, на третьей — отбор рабочих из бригад, попавших в выборку на второй ступени, отбора, и т. д.
Необходимость многоступенчатого отбора вызвана, как правило, отсутствием информации о всех единицах генеральной совокупности. При многоступенчатом отборе для организации первой ступени необходимо иметь информацию о распределении того или иного признака по всей совокупности единиц отбора первой ступени. Для организации второй ступени нужна уже только информация об отобранных единицах первой ступени.
На первой ступени, как правило, используется случайный отбора начиная со второй ступени случайно отбирается количество единиц, пропорциональное размеру соответствующей единицы предыдущей ступени и т. д.
Доли отбора на каждой ступени комбинируются таким образом, чтобы в целом доля отбора выборки обеспечивала всем единицам генеральной совокупности равные шансы попасть в выборку.
Пропорциональный способ организации многоступенчатой выборки имеет определенные неудобства. Социолог, с одной стороны, уменьшает объем выборки в целях экономии средств и сокращения сроков проведения исследования, а с другой, — соблюдая принцип пропорциональности, он может получить очень малочисленные группировки по отдельным факторам, которые окажутся недостаточными для статистического анализа.
Существует несколько способов формирования многоступенчатых выборок.
Для примера рассмотрим способ организации двухступенчатой выборки, отбор единиц которой на первой ступени осуществляется с вероятностью, пропорциональной размеру. Воспользуемся для примера условиями и задачами организации выборки в известном исследовании ленинградских социологов.
Единицы первой ступени отбора — предприятия города.
Составляется полный список единиц наблюдений первой ступени отбора — промышленных предприятий и численности молодых рабочих па каждом из них. Генеральная совокупность включала 50 таких предприятий.
| Предприятие (i) | Число молодых рабочих | Накопленные частоты |
| . . . i . . . | N1 N2 . . . Ni . . . N50 | N1 N1 + N2 . . . N1 + N2 + ... + Ni . . . N1 + N2+ ... + N50 = 50 |

|
Единицы отбора ранжируются по численности рабочих, выделенных в качестве единиц наблюдения. Принимается решение о включении в выборку определенного числа заводов, например пяти. По таблице случайных чисел выбирается 5 чисел ( 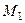 ,
, 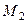 ,
, 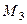 ,
,  и
и 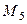 ) между N1 и N (общей кумулированной численностью рабочих в генеральной совокупности); В выборку включаются те предприятия, чьи номера (i) оказались в той же строке (j), которая соответствует кумуляте, содержащей одно из чисел
) между N1 и N (общей кумулированной численностью рабочих в генеральной совокупности); В выборку включаются те предприятия, чьи номера (i) оказались в той же строке (j), которая соответствует кумуляте, содержащей одно из чисел 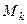 (k = 1¸5), т. е. i = j, если N1 + N2 + ... + Nj-1<
(k = 1¸5), т. е. i = j, если N1 + N2 + ... + Nj-1< 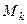 < N1 + N2 + ... + Nj по всем k.
< N1 + N2 + ... + Nj по всем k.
Вторая ступень отбора реализуется, следующим образом. На каждом предприятии, включенном в выборку, выбирается одно и то же число рабочих ( 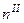 единиц второй ступени отбора). Далее отбор может быть случайным или систематическим.
единиц второй ступени отбора). Далее отбор может быть случайным или систематическим.
Ошибка многоступенчатой выборки (на примере двухступенчатой выборки). При многоступенчатом отборе (начиная с двухступенчатого) следует учитывать специфику расчета ошибки выборки. Каждая ступень отбора делает свой вклад в отклонение находимых оценок от истинных значений характеристик в генеральной совокупности.
Для достаточно большого объема выборки существуют упрощенные формулы расчета средней ошибки.
Для двухступенчатой выборки
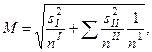 (10)
(10)
где 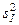 — дисперсия единиц первой ступени отбора и п1 — их численность;
— дисперсия единиц первой ступени отбора и п1 — их численность;  —дисперсия единиц второй ступени отбора и
—дисперсия единиц второй ступени отбора и 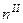 — их численность в составе единиц первой ступени отбора в выборке.
— их численность в составе единиц первой ступени отбора в выборке.
В формуле учтены оба источника ошибок репрезентативности при двухступенчатом отборе. Первый член формулы под корнем указывает па дисперсию, вызванную формированием первой ступени отбора. Второй член указывает па внутригрупповую дисперсию, связанную с организацией второй ступени выборки.
Упрощенность этой формулы состоит в том, что внутригрупповые дисперсии рассчитываются внутри каждой единицы первой ступени после отбора из нее единиц второй ступени. Здесь указана «невзвешенная» средняя из квадратов ошибок по всей сумме единиц второй ступени ( 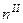 ). Это второй источник случайных ошибок.
). Это второй источник случайных ошибок.
Многофазовый отбор. Многофазовый отбор является особым видом многоступенчатого отбора. Он заключается в том, что из сформированной выборки большего объема производится новая выборка (подвыборка) меньшего объема и т. д.
Особенностью этого способа формирования выборочной совокупности является то, что независимо от числа фаз в последующих подвыборках используется неизменно одна и та же единица отбора, что и в основной выборке.
К многофазовому отбору прибегают тогда, когда в рамках исследования, которое проводится на большой выборке, возникает необходимость тщательного изучения более узкого круга вопросов. Для этих целей формируется вторая фаза — та же выборка в миниатюре и т. д.
Как и в многоступенчатых выборках, при многофазовом отборе каждая фаза является источником случайных ошибок.
Пример двухфазовой стратифицированной выборки[121]. В ходе, исследования сельского населения возникла необходимость более углубленно изучить его культурные потребности и материальные затраты на потребление культуры.
Основная выборка (п) была сделана из стратифицированной генеральной совокупности — изучаемый регион был разделен на 5 трат по типу хозяйств: от мелких (1) до самых крупных (5). Вторая фаза выборки ( 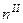 ) была организована из этой основной.
) была организована из этой основной.
| Тип хозяйств | Число людей в первой фазе выборки | Число людей во второй фазе выборки |
| n = 2072 | 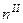 = 400 = 400
|
При исчислении выборочных показателей по выборке необходимо учитывать оба компонента случайной ошибки (как и в случае двухступенчатого отбора), связанного со структурой выборки первой фазы (n) и второй фазы ( 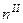 ).
).
Комбинированные выборки. Соединение в многоступенчатой выборке различных приемов отбора (простого случайного, систематического или серийного) делает выборку комбинированной.
Как уже указывалось, большинство используемых в современных социологических исследованиях выборок являются комбинированными.
Одноступенчатая стратифицированная выборка. Комбинированная одноступенчатая выборка использовалась социологами ИСИ АН СССР при формировании выборочной совокупности для изучения индивидуальной производительности труда (индивидуальных норм выработки) рабочих сдельщиков.
Пример. На основе предварительного анализа пилотажного массива из шести возможных для формирования выборки признаков {возраст, образование, стаж по профессии и на данном заводе, заработная плата и квалификация) были выбраны два—заработная плата и стаж по профессии. Эти признаки обнаружили наибольшее влияние на изучаемый показатель — норму выработки[122].
Генеральная совокупность была стратифицирована на 6 страт, различающихся уровнем заработной платы.
Отбор в стратах имел случайный характер — по распределению второго по весу признака (стаж по профессии).
Были известны следующие данные по генеральной совокупности.
| № группы | Заработная плата, руб. | Численность рабочих | № группы | Стаж по профессии, лет. | Численность рабочих | |
| 60-80 81-100 101-130 131-160 Более 160 | 1-2 3-4 5-10 11-16 Более 16 | |||||
| å = 1100 | å = 1100 |
Размер выборки для бесповторного отбора был определен по формуле (см. табл. 16).
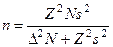
где 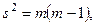 m — выборочная доля. Дисперсия качественного признака (выполнение нормы сдельщиками) при отсутствии информации была принята равной
m — выборочная доля. Дисперсия качественного признака (выполнение нормы сдельщиками) при отсутствии информации была принята равной 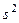 = 0,5*0,5 = 0,25. Доверительная вероятность 1 — a = 0,95; предельная ошибка репрезентативности D = 0,05.
= 0,5*0,5 = 0,25. Доверительная вероятность 1 — a = 0,95; предельная ошибка репрезентативности D = 0,05.
В связи с тем что построение репрезентативной районированной выборки означает сохранение в выборке пропорции для групп генеральной совокупности, для определения размера групп выборочной совокупности принимается следующий план[123]: 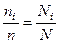 , где N и п — размеры соответственно генеральной совокупности и выборки;
, где N и п — размеры соответственно генеральной совокупности и выборки;  и
и  — размеры соответственно страт в генеральной и выборочной совокупностях. Рассчитывается численность каждой страты (представительство групп заработной платы) в выборке
— размеры соответственно страт в генеральной и выборочной совокупностях. Рассчитывается численность каждой страты (представительство групп заработной платы) в выборке
 .
.
Пропорциональнее построение выборки соответствовало следующим необходимым размерам групп:
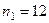 ,
,  ,
, 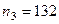 ,
, 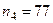 ,
, 
Следующая стадия работы заключалась в расчете доли для страт стажа.
Для пропорционального построения выборки отбор по стажу следует согласовать с планом:  ,
,
где 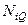 — численность каждой страты по стажу в отдельной страте по уровню зарплаты в генеральной совокупности,
— численность каждой страты по стажу в отдельной страте по уровню зарплаты в генеральной совокупности,  — соответственно для выборки.
— соответственно для выборки.
Когда найдены эти доли для каждой страты по стажу, рассчитывается, сколько единиц наблюдения и с каким стажем должно попасть из каждой такой страты в выборочную совокупность. Например, доля для стажа 1 — 2 года и заработной платы 60 — 80 руб. равна 0,60, а для стажа 3 — 4 года в той же типической группе доля равна 0,40. Исходя из них, находим размер выборки для каждой страты:
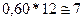 и
и 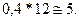
Аналогичный расчет производится по всем остальным стратам, В результате формируется план пропорциональной выборки в абсолютных числах и процентах (табл. 20).
По таблице случайных чисел выбираются случайные числа в соответствии с размером каждой группы, представленной в выборке (табл. 20).
Предварительно картотека была стратифицирована по группам заработной платы и карточки пронумерованы. Из каждой группы выбирались карточки, соответствующие случайным числам. Если стаж на выбранной карточке должен был быть представлен в группе, карточка отбиралась в выборку. Если стаж не должен, был быть представлен в данной группе, карточка возвращалась в генеральную совокупность.
Появление карточек, которые возвращались в массив, потребовало дополнительного выбора случайных чисел для каждой группы, пока не был обеспечен намеченный по плану размер. Как видно из табл. 20, некоторые смещения оказались в группах с большим стажем. Но выборка репрезентативна по контролируемому признаку — средней норме выработки: в генеральной совокупности—109%, в выборке—108,9%.
Таблица 20.План выборки
| Стаж по профессии, лет | Численность выработки в группах по уровню заработной платы | Всего | % генеральной совокупности | % в окончательной выборке | ||||
| 1 – 2 3 – 4 5 – 10 11 – 16 Больше 16 | 14,9 9,9 34,6 15,2 25,3 | 14,8 9,6 36,4 16,5 22,7 | ||||||

| 99,9 | 100,0 |
Рассчитаем по этой выборке оценку доли перевыполняющих план выработки в генеральной совокупности[124] (табл. 21).
Таблица 21. Распределение численности выполняющих план (выборочные данные)
| Группа зарплаты | Выполняют план, абс. цифры 
| Перевыполняют план | Общий объем группы, абс. цифры 
| |
абс. цифры 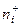
| доли 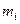
| |||
| 0,33 0,51 0,84 0,935 1,00 | ||||
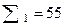
| 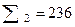
| 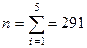
|
Общая доля рабочих, перевыполняющих план, равна

Чтобы использовать показатель доли по выборке как оценку соответствующего параметра в генеральной совокупности, необходимо рассчитать среднюю ошибку выборки.
Расчет дисперсии доли в стратифицированной выборке производится по формуле
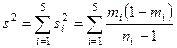 (11)
(11)
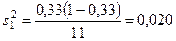 ;
; 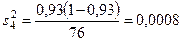 ;
;
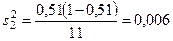 ;
; 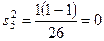 ;
;
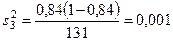 ;
; 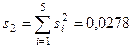 , или 2,78%.
, или 2,78%.
Расчет средней ошибки выборки производится по формуле
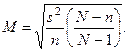 (12
(12

При доверительной вероятности 0,95 предельная ошибка выборки D = ZМ = 1,96 * 0,0084 = 0,016, или 1,6%.
Таким образом, с вероятностью 0,95 можно утверждать, что доля перевыполняющих план будет в интервале (81 ± 1,6)%.
6. Неслучайные методы отбора и другие подходы к построению выборки
Выборочный метод в условиях недостатка информации о генеральной совокупности. Недостаток информации о генеральной совокупности в той или, иной форме свойствен любому выборочному исследованию (для восполнения недостатка оно и проводится).
Будем выделять два типа априорной информации о генеральной: совокупности: а) есть перечень объектов генеральной совокупности и нет сведений о дисперсии изучаемой характеристики, б) нет перечня объектов генеральной совокупности.
В случае а) недостаток информации, как это уже отмечалось выше, преодолевается путем проведения одного - двух пробных исследований.
Для планирования пробных исследований можно рекомендовать использование таблицы достаточно больших чисел[125]. Один из вариантов таких таблиц задает численность выборки, рассчитанную на основе закона больших чисел безотносительно к объему генеральной совокупности. Если известен коэффициент вариации генеральной совокупности, то объем выборки может быть определен по номограммам достаточно больших чисел.
Если генеральная совокупность позволяет найти размах колебания признака, то естественно воспользоваться приближенным расчетом дисперсии с помощью табл. 17.
Дата добавления: 2015-09-29; просмотров: 1256;
